{
    "cells": [
        {
            "cell_type": "markdown",
            "id": "665cadf4",
            "metadata": {},
            "source": [
                "# Gradients, Parallelization and Precision\n",
                "\n",
                "This section describes how to obtain gradients for more efficient optimization and how to speedup execution via parallelization."
            ]
        },
        {
            "cell_type": "markdown",
            "id": "e643ae8c",
            "metadata": {},
            "source": [
                "**Install PyWake if needed**"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 1,
            "id": "d977451d",
            "metadata": {},
            "outputs": [],
            "source": [
                "# Install PyWake if needed\n",
                "try:\n",
                "    import py_wake\n",
                "except ModuleNotFoundError:\n",
                "    !pip install git+https://gitlab.windenergy.dtu.dk/TOPFARM/PyWake.git"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "de1f4cc5",
            "metadata": {},
            "source": [
                "## Gradients\n",
                "\n",
                "PyWake supports three methods for computing gradients:\n",
                "\n",
                "\n",
                "| Method               | Pro                                  | Con |\n",
                "| :------               | :---                                  | :--- |\n",
                "| Finite difference (`fd`)   | - Works out of the box in most cases<br>- Fast for small problems | - Less accurate <br>- Sensitive to stepsize<br>- Requires `n+1` function evaluation |\n",
                "| Complex step (`cs`)        | - More accurate<br>- Works out of the box or with a few minor changes<br> - Fast for small problems | - Requires `n` function evaluations\n",
                "| Automatic differentiation (`autograd`)           | - Exact result<br>- Requires 1 smart function evaluation | - `numpy` must be replaced with `autograd.numpy`<br>- Often code changes and debugging is required<br>- Debugging is very hard<br>- Gradient functions (e.g. using `fd` or `cs`) must be specified if `autograd` fails\n",
                "\n"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "b9f7b105",
            "metadata": {},
            "source": [
                "**Example problem**\n",
                "\n",
                "To demonstrate the three methods we first define an example function, `f(x)`, with one input vector of three elements, `x = [1,2,3]`\n",
                "\n",
                "$f(x)=\\sum_x{2x^3\\sin(x)}$"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 2,
            "id": "ad450706",
            "metadata": {},
            "outputs": [],
            "source": [
                "%load_ext py_wake.utils.notebook_extensions\n",
                "import numpy as np\n",
                "import matplotlib.pyplot as plt\n",
                "\n",
                "def f(x):\n",
                "    return np.sum((2 * x**3) * np.sin(x))\n",
                "\n",
                "def df(x):\n",
                "    # analytical gradient used for comparison\n",
                "    return 6*x**2 * np.sin(x)  + 2*x**3 * np.cos(x)\n",
                "\n",
                "x = np.array([1,2,3], dtype=float)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "77f4e1f7",
            "metadata": {},
            "source": [
                "**Plot variation+gradients of** `f` **with respect to** $x_0, x_1, x_2$"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 3,
            "id": "2f374054",
            "metadata": {},
            "outputs": [
                {
                    "data": {
                        "text/plain": [
                            "<matplotlib.legend.Legend at 0x2e0e94532b0>"
                        ]
                    },
                    "execution_count": 3,
                    "metadata": {},
                    "output_type": "execute_result"
                },
                {
                    "data": {
                        "image/png": "iVBORw0KGgoAAAANSUhEUgAAAh8AAAGiCAYAAABH4aTnAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAA9hAAAPYQGoP6dpAABywklEQVR4nO3deXhU1fnA8e+dyWSyB0L2hRCWgKxCwioKskQBAUWsSqugVbGKSqm1Ij8VbBFrW5RKpVopWBVBZXEBAlHZFJA17DsJBEjISvZlMnN/f4wZjQkwk8yW5P08zzxk7px75p2TS/LmnHPPUVRVVRFCCCGEcBKNqwMQQgghRMsiyYcQQgghnEqSDyGEEEI4lSQfQgghhHAqST6EEEII4VSSfAghhBDCqST5EEIIIYRTSfIhhBBCCKeS5EMIIYQQTiXJhxBCCCGcqlHJx7x581AUhenTp1uOqarK7NmziYyMxNvbm6FDh3LkyJHGximEEEKIZqLBycfu3bt599136dmzZ63jr7/+OvPnz2fhwoXs3r2b8PBwRo4cSXFxcaODFUIIIUTT16Dko6SkhF//+tf85z//oXXr1pbjqqry5ptvMmvWLCZMmED37t15//33KSsrY9myZXYLWgghhBBNl0dDTnryyScZM2YMI0aM4C9/+YvleFpaGllZWSQlJVmO6fV6hgwZwvbt25k6dWqduiorK6msrLQ8N5lM5Ofn06ZNGxRFaUh4QgghhHAyVVUpLi4mMjISjebafRs2Jx/Lly9n37597N69u85rWVlZAISFhdU6HhYWxrlz5+qtb968ecyZM8fWMIQQQgjhhjIyMoiOjr5mGZuSj4yMDJ555hk2btyIl5fXVcv9ssdCVdWr9mLMnDmTGTNmWJ4XFhbStm1b0tLS8Pf3tyW86zIYDGzatIlbb70VnU5n17qbG2kr60lbWU/ayjaOaq/X97xOYWUhD3Z9kM6tO9utXleSa8t6jmqr4uJi4uLirPrdbVPysXfvXrKzs0lISLAcMxqNbN26lYULF3LixAnA3AMSERFhKZOdnV2nN6SGXq9Hr9fXOR4UFERAQIAt4V2XwWDAx8eHNm3ayMV5HdJW1pO2sp60lW0c1V6vJb3W7Ia15dqynqPaqqYua64tmyacDh8+nEOHDpGammp5JCYm8utf/5rU1FTat29PeHg4KSkplnOqqqrYsmULgwYNsvFjCCGEcITmlniIpsemng9/f3+6d+9e65ivry9t2rSxHJ8+fTqvvvoqnTp1olOnTrz66qv4+PgwadIk+0UthBCi0c4XnedkwUlGxI5wdSiihWnQ3S7X8txzz1FeXs4TTzxBQUEB/fv3Z+PGjXafvyGEEKLhThac5O4v7sbbw5tBkYPw0fm4OiTRgjQ6+di8eXOt54qiMHv2bGbPnt3Yqq9KVVWqq6sxGo02nWcwGPDw8KCiosLmc1saZ7aVVqvFw8NDuoKFcKJOrToR4x9DRnEG32Z8yx3t73B1SKIFsXvPh6NVVVWRmZlJWVmZzeeqqkp4eDgZGRnyi+46nN1WPj4+RERE4Onp6fD3EkKY/1Ac034M/z7wb9aeXSvJh3CqJpV8mEwm0tLS0Gq1REZG4unpadMvRpPJRElJCX5+ftddAKWlc1ZbqapKVVUVOTk5pKWl0alTJ/neCOEko+NG8+8D/2bHpR3klefRxruNq0MSLUSTSj6qqqowmUzExMTg42P7+KTJZKKqqgovLy/5BXcdzmwrb29vdDod586ds7ynEMLx4gLj6NqmK0fzjrIhfQOTbpAbA4RzNMnfwJI4ND/yPRXCNcbEjQFgXdo6F0ciWhL5iS+EEC3YqLhRaBQNZ66cobCy0NXhiBaiSQ27CCGEsK8QnxD+M/I/9AzpiZeHDHkK55DkQwghWrh+Ef1cHYJoYWTYRQghBPDj3WfGKleHIVoAST6cSFVVHnvsMYKCglAUhdTUVPLy8ggNDSU9Pd1SbujQoSiKYinTlEyZMsUS+5o1awCYOHEi8+fPd21gQohr+vrc14z/fDz/3PdPV4ciWgBJPpwoOTmZpUuX8tVXX5GZmUn37t2ZN28eY8eOpV27drXKPvroo5Yy9jZv3jz69u2Lv78/oaGh3HnnnZYdia9l0aJF9OzZk4CAAAICAhg4cCDr16+vVWbBggVkZmbWOvbSSy8xd+5cioqK7Po5hBD2oygKaYVprE9bj9EkK0ALx5Lkw4nOnDlDREQEgwYNIjw8HIPBwOLFi3nkkUfqlPXx8SE8PBwPD/tPy9myZQtPPvkkO3fuJCUlherqapKSkigtLb3medHR0bz22mvs2bOHPXv2MGzYMMaPH8+RI0csZQIDAwkPD691Xs+ePWnXrh0fffSR3T+LEMI+bo66GX9Pf7LLs9lzeY+rwxHNXJNPPlRVpayq2upHeZXRpvLXeqiqanWcU6ZM4amnnuL8+fMoikK7du1Yv349Hh4eDBw48Lrnf/zxx3h5eXHx4kXLsUceeYSePXtSWGjb7XHJyclMmTKFbt260atXL5YsWcL58+fZu3fvNc8bO3Yso0ePJj4+nvj4eObOnYufnx87d+687nuOGzeOjz/+2KY4hRDO46n1JCk2CYC1Z9e6OBrR3DX5u13KDUa6vrTBJe999JXb8PG0rgkXLFhAhw4dePfdd9m9ezdarZa5c+eSmJho1fn33Xcfr732GvPmzWPhwoXMmTOHDRs2sHPnTgIDAxvzMSzJS1BQkNXnGI1GPv30U0pLS61Knvr168e8efOorKxEr9c3OFYhhOOMaT+GladWknIuhVkDZqHXyv9V4RhNvuejqQgMDMTf3x+tVkt4eDghISGkp6cTGRlp1fmKojB37lzee+89Xn31VRYsWEBycjJRUVEAfPXVV3Tu3JlOnTrx3nvvWR2XqqrMmDGDwYMHWzW/5NChQ/j5+aHX63n88cdZvXo1Xbt2ve55UVFRVFZWkpWVZXVsQgjnSghLIMwnjBJDCVsvbHV1OKIZa/I9H946LUdfuc2qsiaTieKiYvwD/O2ynLe3Ttuo88vLy23ax+SOO+6ga9euzJkzh40bN9KtWzcAqqurmTFjBps2bSIgIIA+ffowYcIEq3oypk2bxsGDB/nuu++siqFz586kpqZy5coVVq5cyeTJk9myZct1ExBvb2+ABu1GLIRwDo2iYXTcaJYcWcK6s+sYGTvS1SGJZqrJJx+Kolg99GEymaj21OLj6eEWe4kEBwdTUFBgdfkNGzZw/PhxjEYjYWFhluO7du2iW7dull6Q0aNHs2HDBu6///5r1vfUU0/xxRdfsHXrVqKjo62KwdPTk44dOwKQmJjI7t27WbBgAe+88841z8vPzwcgJCTEqvcRQrjGHR3uILc8l3Edx7k6FNGMuf43cAvWu3dvjh49alXZffv2cc899/DOO+9w22238eKLL1peu3TpkiXxAPNdKT+fmPpLqqoybdo0Vq1axbfffktcXFyDP4OqqlRWVl633OHDh4mOjiY4OLjB7yWEcLz41vG8evOrDIgY4OpQRDPW5Hs+mrLbbruNmTNnUlBQQOvWra9aLj09nTFjxvD888/zwAMP0LVrV/r27cvevXtJSEio964bRVGuWt+TTz7JsmXL+Pzzz/H397fMwwgMDLQMj9TnhRdeYNSoUcTExFBcXMzy5cvZvHkzycnJ1/2s27ZtIykp6brlhBBCNH/S8+FCPXr0IDExkU8++eSqZfLz8xk1ahTjxo3jhRdeACAhIYGxY8cya9YswDyZ8+c9HRcuXCAiIsLyfOnSpbWSkUWLFlFYWMjQoUOJiIiwPFasWFHrnF8mRJcvX+aBBx6gc+fODB8+nB9++IHk5GRGjrz2uHBFRQWrV6/m0UcftaJVhBDu4Hj+cf6+++9cLr3s6lBEMyQ9H040ffp0pk+fXuvYiy++yLPPPsujjz5a7zyUoKAgjh07Vuf4559/bvm6X79+HD58mIsXLxIQEMC6det46aWXLK+np6czZMgQy3Nr1ic5d+4cN910U61jixcvvu559Vm8eDH9+/dnwADpxhWiqZj3wzz2Ze8jxCeEyd0muzoc0cxIz4eLjR49mqlTp9aZo/H222/j5+fHoUOHrluHh4cH//jHP7j11lvp3bs3f/zjH2nTpo3l9Q0bNvD666/bFNfGjRuZM2eOTecAPP744/j5+dU6ptPpeOutt2yuSwjhOmPajwFkwTHhGNLz4QaeeeaZWs8/+ugjysvLAWjbtq1VdYwbN45x4+qfnb5jxw6bY/r+++8btBfLK6+8wrPPPgtgGfp57LHHbK5HCOFaSbFJzPthHsfyj3H2ylnat2rv6pBEMyI9H24oKiqKjh070rFjRzw9PV0djk1CQ0Mtsfv6+ro6HCFEA7XyasXgqMEAfHX2KxdHI5obST6EEELUa3T70QCsS1tn015WQlyPJB9CCCHqNTRmKD4ePlwsuciBnAOuDkc0I5J8CCGEqJe3hzfD2w4nyCuIy2Vyy62wH5lwKoQQ4qqe6/scvp6+6DQ6V4cimhFJPoQQQlxVK69Wrg5BNEMy7CKEEOK6TKqJs1fOujoM0UxI8iGEEOKaLpdeJumzJO5bex9lhjJXhyOaAUk+hBBCXFOoTyieWk/Kq8v5NuNbV4cjmgFJPoQQQlyToiiy3LqwK0k+nEhVVR577DGCgoJQFIXU1FTy8vIIDQ0lPT3dUm7o0KEoimIp05RMmTLFEvuaNWsAmDhxIvPnz3dtYEKIRhkTZ04+dlzaQV55noujEU2dJB9OlJyczNKlS/nqq6/IzMyke/fuzJs3j7Fjx9KuXbtaZR999FFLGYCtW7cyduxYIiMja/1id6ZFixbRs2dPAgICCAgIYODAgaxfv75WmQULFpCZmVnr2EsvvcTcuXMbtFeMEMI9tAtsR7c23TCqRjakb3B1OKKJa/rJh6pCVan1D0OZbeWv9bBxueEzZ84QERHBoEGDCA8Px2AwsHjxYh555JE6ZX18fAgPD8fDw3w3dGlpKb169WLhwoV2abaGiI6O5rXXXmPPnj3s2bOHYcOGMX78eI4cOWIpExgYSHh4eK3zevbsSbt27fjoo4+cHbIQwo4sQy9pMvQiGsemdT4WLVrEokWLLEME3bp146WXXmLUqFGAucv9/fffr3VO//792blzp32irY+hDF6NtKqoBmhlz/d+4RJ4Wrd52s/bRlEUYmNjmT9/Ph4eHgwcOPC6548aNcrSztb6+OOPeeihhzhz5gxRUVEAPPLII+zatYtt27YRGBhoU31jx46t9Xzu3LksWrSInTt30q1bt2ueO27cOD7++GN+97vf2fSeQgj3cXu72/n7nr9zMOcgGcUZxPjHuDok0UTZ1PNhzV++t99+O5mZmZbHunXr7B50U7RgwQJeeeUVoqOjyczMZPfu3WzdupXExESHved9991H586dmTdvHgBz5sxhw4YNrF+/3ubE45eMRiPLly+ntLTUquSpX79+7Nq1i8rKyka9rxDCdUJ8Qniu73N8MOoDov2iXR2OaMJs6vmw5i9fvV5fp9vdoXQ+5h4IK5hMJoqKiwnw90ejscOIk87H6qKBgYH4+/uj1Wot7ZOenk5kpHW9Ng2hKApz585l4sSJREZGsmDBArZt22bpBQG466672Lx5M8OHD+ezzz67bp2HDh1i4MCBVFRU4Ofnx+rVq+natet1z4uKiqKyspKsrCxiY2Mb9bmEEK7z6xt+7eoQRDPQ4OXVjUYjn376aZ2/fDdv3kxoaCitWrViyJAhzJ07l9DQ0KvWU1lZWeuv4ZpJiQaDAYPBUKuswWBAVVVMJhMmk+lnn8LbqphVVQWdEVXng0lRrDrnOhXaNO+jZkvqmtjLysqIjIys/Vl+Vra+4zXqtMFVjB49mq5duzJnzhySk5O54YYbap03bdo0pkyZwv/+979ax2ti/WUcnTp1Yt++fVy5coVVq1YxefJkNm3aVG8C8vMY9Xo9ACUlJfXGbTKZUFUVg8GAVqu97udyJzXX6S+vV1GXtJX1juYdZeWplVRXVhOWGUa3kG54eXi5Oiy3JdeW9RzVVrbUZ3Pyca2/fEeNGsU999xDbGwsaWlpvPjiiwwbNoy9e/dafvn80rx585gzZ06d4xs3bsTHp3bPgoeHB+Hh4ZSUlFBVVWVr6BbFxcUNPrcxKioqzL0vPyZYgYGBZGdn17kLpLq6mqqqqmveHVJeXm7V3SPffPMNx48fx2g04uvrW+echIQEvvvuO6qrq+utr762Cg0NJTQ0lOeff56dO3fy97//nTfffPOaMWZkZADg5eVV7/tUVVVRXl7O1q1bqa6uvu7nckcpKSmuDqHJkLa6vu0V21lXYR62/nLTl2jQEKWNooNHBzrrOhOljUKjuOaegcvGy+yo3EGgJpBbvW51SQxXI9eW9ezdVmVl1q9+a3Py0blzZ1JTU7ly5QorV65k8uTJbNmyha5du3LvvfdaynXv3p3ExERiY2NZu3YtEyZMqLe+mTNnMmPGDMvzoqIiYmJiSEpKIiAgoFbZiooKMjIy8PPzw8vL9r8AVFWluLgYf39/FHv0fNjIy8sLjUZj+Vz9+vXjo48+qvM5PTw88PT0rHP857y9va/5OsC+fft46KGHWLRoEStWrOD111/nk08+qVPOx8cHDw+PWvVZ21ZarRZVVeuN5ecxpqWlER0dTVxcXL31VFRU4O3tzS233NKg760rGQwGUlJSGDlyJDqd7Px5LdJW1ovJjSHkfAg7T+8k1yOXvIo8MowZZBgz2Fy5mWDvYEbGjOSO9nfQpXUXp/5M25Sxibe2vUWIdwiv3f4aWo3reyvl2rKeo9rKluUUbE4+PD096dixIwCJiYns3r2bBQsW8M4779QpGxERQWxsLKdOnbpqfXq9vt5eEZ1OV6dRjEYjiqKg0WgaNGejpru/pg5nq/nhUPPet99+Oy+88AKFhYW0bt26Ttmfx1hSUsLp06ctz8+dO8fBgwcJCgqibdu2dd4rPT2dsWPH8vzzzzN58mS6d+9O37592b9/PwkJCbXKajSaOu9XX1u98MILjBo1ipiYGIqLi1m+fDmbN28mOTm53vb8+ffp+++/Jykp6artXhNDfd/3pqIpx+5s0lbX1yeiDz2Ce9ApqxOjRo0ipyqHXZm72H5pO99f/J7c8lw+PvkxH5/8mBuCbuD+Lvczpv0YPLWeDo9taOxQ/H/wJ6c8hwP5B+gf0d/h72ktubasZ++2sqWuRv8GVlX1qncw5OXlkZGRQURERGPfplnq0aMHiYmJ9fZG/NKePXvo3bs3vXv3BmDGjBn07t2bl156yVJm6dKlKIpCfn4+o0aNYty4cbzwwguAeXhl7NixzJo1y6rYli5dWichunz5Mg888ACdO3dm+PDh/PDDDyQnJzNy5Mhr1lVRUcHq1at59NFHrXpvIURtiqIQ5RfFXZ3u4m9D/saWe7ewcNhCbm93O54aT47lH+Ol7S9x28rbWHp4KeXV5Q6Nx1PrSVJsEiDLrYuGsann41p/+ZaUlDB79mzuvvtuIiIiSE9P54UXXiA4OJi77rrLUfE3KdOnT2f69Om1jr344os8++yzPProo9fsjRk6dKhlEujVpKenM2TIEIKCgjh27Fid1z///HOrYz137hw33XRTrWOLFy+2+vxfnte/f38GDBjQoPOFELXptDqGxAxhSMwQrlRcYdXpVSw7tozLZZf5x95/sOTIEn7X63fcHX83Oo1jegHGtB/DylMrSTmXwqwBs9Br65/XJ0R9bOr5uNZfvlqtlkOHDjF+/Hji4+OZPHky8fHx7NixA39/f0fF3+SNHj2aqVOncvHixVrH3377bfz8/Dh06JDVdW3YsIHXX3/dpve/7bbbuOeee1i3bh3R0dHs3r0bME/4rW8i8PU8/vjj+Pn51Tqm0+l46623bK5LCHF9rbxa8XD3h1k/YT2vDHqFKL8o8ivymfvDXCZ+MZGdmY5Z5DEhLIEwnzBKDCVsvbDVIe8hmi+bej6u9Zevt7c3GzbIev8N8cwzz9R6/tFHH1Febu42rW8+x9Xs2LHD5ve+2vfs+++/b9BeLK+88grPPvssgGW47bHHHrO5HiGEbXRaHXd1uos7OtzBZyc/Y1HqIs4WnuXRjY8ypv0Ynuv7HEFeQXZ7P42iYXTcaJYcWcLas2sZGXvt4Vchfq7p7+3SDEVFRdGxY0c6duyIp6fjJ4/ZU2hoqCV2X1/rlp4XQtiPTqPj/i7389WEr5jUZRIaRcPas2u56/O7+ObcN3Z9rzHtxxDlF0XnoM52rVc0f5J8CCFEMxTgGcDM/jP5aPRHdGrdifyKfKZvns7s7bPtNiE1vnU86yes53e9ZM8mYRtJPoQQohnrHtyd5WOW83D3h1FQWHlqJfd/dT9phWmNrltRFJesmSSaPkk+hBCimfPUevL7hN/zn6T/EOwdzJnCM9y/9n42nd9kl/oNRgObMzaTW55rl/pE8yfJhxBCtBD9I/rz6dhPSQxLpNRQyjObnmHxocXXvY3/eqZvns5T3z4la34Iq0nyIYQQLUiwdzDvJr3LfZ3vQ0XlzX1vMmfHHKpNDd9TaUj0EEAWHBPWk+RDCCFaGJ1Gx6wBs5jZbyYaRcPKUyv5/abfU1Fd0aD6kmKT8FA8OJZ/jLNXzto5WtEcSfIhhBAt1KQbJvHG0DfQa/VsvrCZ3339O0oNpTbX08qrFYOjBgPw1dmv7B2maIYk+RBCiBZsWNth/HvEv/HT+bHn8h6mpkyluKrY5nrGtB8DwLq0dY2eQyKaP0k+nEhVVR577DGCgoJQFIXU1FTy8vIIDQ0lPT3dUm7o0KGWW9hSU1NdFm9DTJkyxRL7mjVrAJg4cSLz5893bWBCiKtKDE/kvaT3CPAM4EDOAR7/+nGbe0CGxAzBx8OHiyUXOZBzwEGRiuZCkg8nSk5OZunSpXz11VdkZmbSvXt35s2bx9ixY2nXrl2tso8++qilDMDWrVsZO3YskZGRtX6xX8u8efPo27cv/v7+hIaGcuedd3LixAkHfLKfLFiwgMzMzFrHXnrpJebOndug5dqFEM7RLbgbi29bTIBnAAdzDvLE10/YtBiZt4c3w9sOB3DYfjKi+ZDkw4nOnDlDREQEgwYNIjw8HIPBwOLFi3nkkUfqlPXx8SE8PBwPD/P2O6WlpfTq1YuFCxda/X5btmzhySefZOfOnaSkpFBdXU1SUhKlpbaP6VorMDCQ8PDwWsd69uxJu3bt+Oijjxz2vkKIxusS1IV3k97FX+fPvux9zNg8A4PRYPX5j/R8hFXjVvF4r8cdGKVoDmzaWM4dqapqdXZuMpkory7Hw+Bxze3rreXt4W316n5Tpkzh/fffB8yrAsbGxjJ//nw8PDwYOHDgdc8fNWoUo0aNsim+5OTkWs+XLFlCaGgoe/fu5ZZbbrnqeR9//DEPPfQQ+/btIyAgAIBHHnmEXbt2sW3bNgIDA22KA2DcuHF8/PHH/O53sgyzEO6sW5tu/GvEv3hs42N8d/E7Xtz+Iq8OfhWNcv2fme0D2zshQtEcNPnko7y6nP7L+rvkvX+Y9AM+Oh+ryi5YsIAOHTrw7rvvsnv3brRaLXPnziUxMdHBUf6ksLAQgKCga+9sed999/Haa6/xxhtv8M477zBnzhw2bNjAzp07G5R4APTr14958+ZRWVmJXq9vUB1CCOfoHdqbN259g6e+MS8cFuYTxu8Tfm9THQaTAZ1G56AIRVMnwy5OEhgYiL+/P1qtlvDwcEJCQkhPTycyMtIp76+qKjNmzGDw4MGWeSRXoygKf/7zn/nggw+YN28eCxYsIDk5maioKDIyMhg6dChdu3alZ8+efPrpp1a9f1RUFJWVlWRlZdnj4wghHGxw1GBeHvQyAP89/F9Wnlxp1XmlhlKe2/ocIz4dQZmhzJEhiiasyfd8eHt488OkH6wqazKZKC4uxt/f327DLo1RXl6Ol5dXo+OwxrRp0zh48CDfffedVeXvuOMOOnfuzCuvvMLGjRvp1q0bAB4eHrz55pvceOONZGdn06dPH0aPHo2vr+816/P2NrdVWZn8MBKiqbiz451klmTy9oG3+cvOvxDtH03/iGv3NPt4+HA49zD5Ffl8m/Etd7S/w0nRiqakyfd8KIqCj87H6oe3h7dN5a/1aOxujsHBwRQUFNipJa7uqaee4osvvmDTpk1ER0dbdc6GDRs4deoURqORsLAwy/GIiAhuvPFGAEJDQwkKCiI/P/+69dWUCQkJsf0DCCFc5vFejzM6bjTVajV/2PIHLhRfuGZ5RVEsa37Icuviapp88tGU9e7dm6NHjzqsflVVmTZtGqtWreLbb78lLi7OqvP27dvHvffey/z580lKSuLFF1+st9yePXswmUzExMRct87Dhw8THR1NcHCwTZ9BCOFaiqLwyk2v0L1NdworC3l609PXHU4ZE2dOPnZc2kFeeZ4zwhRNjCQfLnTbbbdx5MgRq3o/SkpKSE1NtSw6lpaWRmpqKufPn7/qOU8++SQffvghy5Ytw9/fn6ysLLKysigvv/rdQenp6YwZM4Y//elP3HfffcyZM4eVK1eyd+/eWuXy8vJ48MEHeffdd636rNu2bSMpKcmqskII96LX6nnz1jcJ9g7mVMEp5uyYc81VTNsFtqNbm24YVSMbz210YqSiqZDkw4V69OhBYmIin3zyyXXL7tmzh969e9O7d28AZsyYQe/evXnppZcsZZYuXVprKGjRokUUFhYydOhQIiIiLI8VK1bUe05+fj6jRo1i3LhxzJw5E4CEhATGjh3LrFmzLOdUVlZy1113MXPmTAYNGnTd2CsqKli9ejWPPvrodcsKIdxTmG8Yfx/yd7SKlnVp61h+Yvk1y8vQi7gWST6caPr06bWWUQd48cUXWbBgASaT6ZrnDh06FFVV6zyWLl1qKZOens6QIUMsz+srr6oqU6ZMqfecoKAgjh07xjvvvFPrvT///HPLmiE15w8bNowHHnjAqs+9ePFi+vfvz4ABA6wqL4RwTwlhCcxImAHA33b/jSN5R65a9vZ2t6NRNBzIOUBGcYazQhRNhCQfLjZ69GimTp3KxYsXax1/++238fPz49ChQ1bXtWHDBl5//XWb3t/Wc77//ntWrFjBmjVruPHGG7nxxhtrxfj444/j5+dX6xydTsdbb71lU1xCCPf0QNcHGBYzDIPJwLObn6WkqqTeciE+IdwTfw/P9HkGP51fvWVEy9Xkb7VtDp555plazz/66CPLvIy2bdtaXc+OHTtsfm9bzxk8ePA1e2leeeUVnn32WcB8ZwzAY489ZnNcQgj3VDMB9fiXx7lQcoFXf3iVV29+td6y/zfg/5wcnWgqJPlwQ1FRUa4OocFCQ0MJDQ11dRhCCAcK1Afy2i2vMSV5Cl+e/ZKbom6yzPEQwhoy7CKEEMJmvUN7M7XnVADm7pxLVmn9qxeXGcpYe3Ytq0+tdmZ4ws1J8iGEEO7GZIINs1COuvcv7Md6PkaP4B4UG4r5v+//D5Nad0h2Z+ZOnt/2PG/tfwujyeiCKIU7apLJx7XuLxdNk3xPhfiRsRq+mAY7FqL94km8qtx3kS4PjQdzB8/FS+vFD5k/8NnJz+qUGRw1GH9Pf3LKc9hzeY8LohTuqEklHzqdeYdE2R+k+an5ntZ8j4VokQwV8OlkSP0IFC3G0fOp8Gzj6qiuKS4wjmf6mCfN/2PPP7hYUvvOPU+tJ0mx5gUGZc0PUaNJTTjVarW0atWK7OxsAHx8bNtfxWQyUVVVRUVFhV02lmvOnNVWqqpSVlZGdnY2rVq1QqvVOuy9hHBrlSWwfBKkbQGtJ0xcgtrxNriwztWRXdekGyaRci6Ffdn7mLN9Du+MfKfWz+Yx7cew8tRKUs6lMGvALPRavQujFe6gSSUfAOHh4QCWBMQWqqpSXl6Ot7d3ozeFa+6c3VatWrWyfG+FaHFUFVb82px46Hzh/o+h/RAwGFwdmVU0ioZXbnqFu7+4mx2ZO/jy7JeM6zDO8npCWALhvuFklWax9cJWRsaOdGG0wh00ueRDURQiIiIIDQ3FYON/TIPBwNatW7nllluke/86nNlWOp1OejxEy6YoMPj3kHMC7v0IohNcHZHNYgNi+V2v3/Hmvjd5fffrDI4aTJBXEGBOTkbFjWLJ4SWsPbtWkg/R9JKPGlqt1uZfWFqtlurqary8vCT5uA5pKyGcwGSCmmHN9kPh6f2g83ZpSI3xYLcHSU5P5nj+cf6x5x/MHTzX8tqYuDEsObyEkqoSTKoJjSJD3y2ZfPeFEMIVLh+Fd24293bUaMKJB4BOo+PFAS+ioPDFmS/YnbXb8lp863hSJqbw3m3vSeIhJPkQQginu7AHloyCy4dhwwuujsaueob05J74ewD4y86/YDCZh8cVRSHcV+Z1CTNJPoQQwpnObIL3x0HFFYjuCxP+4+qI7O7pPk8T5BXE2cKzLDu2rM7rBRUFFFUVuSAy4S5sSj4WLVpEz549CQgIICAggIEDB7J+/XrL66qqMnv2bCIjI/H29mbo0KEcOXL1LZeFEKJFOfYlLPsVGEqh/a3w4OfgE+TqqOwuUB/I9D7TAVh0YBE5ZTmW1/65758M+2QYq06uclF0wh3YlHxER0fz2muvsWfPHvbs2cOwYcMYP368JcF4/fXXmT9/PgsXLmT37t2Eh4czcuRIiouLHRK8EEI0Gfs/gk8eBGMV3DAOJq0AT19XR+Uw4zuOp2dwT0oNpSzYt8ByPNw3nGq1mnVp7r9+iXAcm5KPsWPHMnr0aOLj44mPj2fu3Ln4+fmxc+dOVFXlzTffZNasWUyYMIHu3bvz/vvvU1ZWxrJldbvdhBCixTAZzauWqibo/RuYuAQ8mvdCWxpFw5/6/QmAz898zuHcwwAkxSbhoXhwLP8YZ6+cdWWIwoUafKut0Wjk008/pbS0lIEDB5KWlkZWVhZJSUmWMnq9niFDhrB9+3amTp1abz2VlZVUVlZanhcVmccBDQaDzet4XE9NffautzmStrKetJX1WnRbTfwfmgPLMPV7HEwqmK7fBk29vW5odQOj241mXfo6XvvhNf478r/4an0ZFDmIrRe38sXpL3iy15N2ea+m3lbO5Ki2sqU+RbVxR69Dhw4xcOBAKioq8PPzY9myZYwePZrt27dz0003cfHiRSIjIy3lH3vsMc6dO8eGDRvqrW/27NnMmTOnzvFly5bh4+NjS2hCCOE+VBNhRQe5HHijqyNxqSJTEW8UvYEBA/f73E83z24crDrIJ2Wf0FrTmhn+M2TF6WairKyMSZMmUVhYSEBAwDXL2tzz0blzZ1JTU7ly5QorV65k8uTJbNmyxfL6Ly8iVVWveWHNnDmTGTNmWJ4XFRURExNDUlLSdYO3lcFgICUlhZEjR8rCWdchbWU9aSvrtZi2MhrQfvU0mrOfYhzxCqb+TzSomubSXgUHC/jP4f+wTbON6bdN51b1Vr5a9RUF1QVE94umV0ivRr9Hc2krZ3BUW9WMXFjD5uTD09OTjh07ApCYmMju3btZsGABf/qTeWwvKyuLiIgIS/ns7GzCwsKuWp9er0evrzv2qdPpHHYBObLu5kbaynrSVtZr1m1lqIBVD8PJ9aBo0QZEom3kZ23q7fVIz0dYfWY1F0ousDptNb++4dcMbzucL89+SfL5ZBIjE+32Xk29rZzJ3m1lS12NXudDVVUqKyuJi4sjPDyclJQUy2tVVVVs2bKFQYMGNfZthBDC/VUUwUcTzYmHhxfctwx63uPqqFzOR+fD73r9DoB3DrxDSVUJ93a5lxf6v8ATNzasV0g0bTb1fLzwwguMGjWKmJgYiouLWb58OZs3byY5ORlFUZg+fTqvvvoqnTp1olOnTrz66qv4+PgwadIkR8UvhBDuoTQPProbLu0HT3+YtBzaDXZ1VG7jrk538cHRD0gvSmfpkaVM6z3NLsMtommyKfm4fPkyDzzwAJmZmQQGBtKzZ0+Sk5MZOdK8Q+Fzzz1HeXk5TzzxBAUFBfTv35+NGzfi7+/vkOCFEMItGCpg6WjIOQ4+beA3KyGyt6ujcis6jY6n+zzNjM0z+N/R/3F/l/tp493G1WEJF7Fp2GXx4sWkp6dTWVlJdnY2X3/9tSXxAPNk09mzZ5OZmUlFRQVbtmyhe/fudg9aCCHcis4L+kyGgCh4KFkSj6sY0XYEXdt0pby6nMWHF1NtquaTE5/w2MbHKDOUuTo84USyt4sQQjTUz1cqGPgEPLEDQuJdF4+bUxSFZ3o/A8CK4yvIKcvh/SPvsyNzB99mfOvi6IQzSfIhhB2UVbs6AuF053+A98dC+ZWfjnkFuiycpmJg5EASwhKoMlWx+PBiRrcfDcDas2tdHJlwJkk+hGgEVVV577t0/rJfS1puqavDEc5y+mv433hI3wab57k6miZFURSevNG8qunKUyvpG9YXgB2XdpBXnufK0IQTSfIhRAMZjCZeWH2Yv244SWm1wrrDl10dknCGI6th2X1QXQ4dR8Dwl10dUZPTN7wv/cP7U20ybzDXrU03jKqRjec2ujo04SSSfAjRAIVlBqYs2cXHu86jKHBXOyNPDIlzdVjC0fa+D589bN6XpdtdcN/H4CnbQDREzfoen5/5nMFR5luSZeil5ZDkQwgbpeWWctei7/n+dB4+nloWTbqRoRHX3kZANAPfL4AvnzbvTJswBe5eDB6ero6qyeoT1sfS+5FZmolG0XAg5wAZxRmuDk04gSQfQthg++lc7vzX95zNKSUy0IvPHh/E8C6hrg5LOFr5FfjhHfPXN02HO94EjdaFATUPU3uZdztfn7aexLBEboq6SW65bSFs3ttFiJZIVVU+3HmO2V8exWhSuTGmFe8+mECov5ds4d0SeLeCB9bAmW9gwO9cHU2z0Te8L31C+7Avex+dWnfi+X7Puzok4STS8yHEdVRVm5i15jAvfn4Eo0nlrt5RLH9sAKH+Xq4OTTiS0QAZu396HhIviYcDPNbzMQBWnVpFQUWBi6MRziLJhxDXkFtSyW/e+4FlP5gnlv7p9i7M/1UvvHTS5d6sVZXB8knmJdPPbHLMe6gqGMrNm9FVFEF1Ze1Fy1qIQZGDuCHoBsqry/no2EdklWaxK3OXq8MSDibDLkJcxcELV5j6wV4yCyvw13uw4P4bGdYlzNVhCUerKDTfSnt+O3h4g6kRK8gVX4asg5B9FPLOwJVzUHQJSnN+XJzsF8mGogXv1uAXBoFRaFq1I6rAAxjdiA/k3hRF4dGej1r2fHn34LsEeweTMjEFrcyrabYk+RCiHp/uyWDWmsNUVZtoH+LLfx5MpEOIn6vDEo5WkgMfTjAnDPpAmLQCYgdaf37eGTi7GdK/g4xdUHTBtvdXjVCWa35kH0ELRAYm2lZHEzQsZhjtAtqRXpSOXqsnpzyH3Zd3MyBigKtDEw4iyYcQP1NVbeLPXx3lg53nABjeJZQ37ruRAC+diyMTDnclAz64E/JOg08wPLAaInpe+xyTCS7shmNfwIn1kH/mFwUUCI6HsK7mf1u3M28+5xdq7uHw9AXNj9eWsQqqSqC8AIoz4UoGxtzTZGYaCHHAx3UnWo2Wyd0mM2fHHDQ/zgZYd3adJB/NmCQfQvwos7CcJz7ax/7zVwCYPqITTw/rhEYj63c0e8VZ8N/bzT0VgTHmO1uCO169fO4pSF0Ghz6Fwp+tS6HRQUx/iLvF3GMS2Qf0VvaY6bzAKwACIiGsGwAmg4EL69ZxnRSoWRjbYSz/Sv0XueW5AKScS2HWgFnotXoXRyYcQZIPIYDvT+fy9Mf7ySutIsDLgzfvk/kdLYpvKLS7CS7ugwfXQGB03TJGg7mHY/diOPf9T8c9/aDzKOhyB3QYZk4ghM30Wj2/vuHXLNi3AA/FgxJDCVsvbGVk7EhXhyYcQJIP0aKZTCpvbz7N/JSTmFToGhHAot/0IbaNr6tDE86k0cD4f0FlMfgE1X6tvAD2LDEvMlaSZT6maMz7utw4CeJvB52382Nuhu6Jv4d3D75LeXU5YF5uXZKP5kmSD9Fi5ZVU8vtPDrD1ZA4A9yRE8+c7u8tttC3FyY1wdA2Me8u8WqlWVzvxKMmBHW+ZezqqSszH/MIg4SHo8yAERrkk7OYsUB/InR3v5OPjHwOwK2sXlcZKGXpphiT5EC3SrrR8nv54P1lFFeg9NPz5zu78KjHG1WEJZzn0Gayear6NNqoP9H3kp9fK8uH7N2HXf6Bmqe/QbjDoKeh+t+zn4mAP3PAAy48vR0Xl3ZHvSuLRTEnyIVoUo0ll0c+GWdqH+PL2r/vQJVzG6VuM3Yth7R8AFXrcA30mm49XlcEPi+C7N6GyyHwssjcM+ZN5aEU2DnSKmIAYhsYMZVPGJtacXkP34O6uDkk4gCQfosW4XFTB71eksv1MHgATekfx5zu746uX/wYtgqrCd/Phm1fMz/s+AqP+Zk4qDn4CX8+Goovm18J6wLD/g/jbJOlwgQe6PsCmjE18ceYLnur9FH46P1lwrJmRn7qiRfj66GX++NkBCsoM+Hhq+fP47tydUM8dDTZSVZXd6QUYW96q2E2LqkLKS7D9n+bnNz9rTi4yD8C6P8KFH5fzDmwLw1+E7hPNk1CFSySGJdK5dWdOFJzgrs/v4sGuDzKl+xRXhyXsSJIP0ayVVxmZu+4oH+48D0C3yADeur837Ru5WumFgjJW7bvIZ3svcD6/jEe7KIy1R8DCMXJPmu9WAUj6i3nC6PrnYPd7oJpA5ws3z4CB08zrbQiXUhSFX9/wa17a/hI55Tl8dfYrST6aGUk+RLN16EIh01fs50xOKQCP3hzHs7d1Ru/R8O7brSdzeGfrGbafybPsAear13Kl0miPkIWjhHSGX70PpbngFQgL+/1022y3CeaERO5ecSuj4kbxtz1/o7iqmBMFJzhz5QwdWnVwdVjCTqRfUTQ71UYTC789xV1vf8+ZnFJC/fX87+F+zBrT1ebEQ1VVqo0my/OMgjK+P21OPAZ1aMP8X/Vi+3NDGBwu4y5up6rUvNdKjagEOLURPnnAnHgEtTevZHrPEkk83JCXhxcT4ydanq89u9aF0Qh7k54P0aycySnhD58cIDXjCgCjuofz6l09aO1r2+2RmYXlrNp3kZV7L/DQTe14YGA7AO7oGUlucRUT+kQRE+QDgMFgsOdHEPZQXgDL7oWCc/BwMlzaB2ufhfJ8886xg6fDLX+UxcHc3H2d72Pp4aWoqJbJp4pMAG4WJPkQzYLJpLJkezqvJx+nstqEv5cHc8Z1467eUVb/sKowGNl49DKf7b3Ad6dyMP3YmfHlgUxL8hHoreOZEZ0c9CmEXZRkwwd3weXDoA+Ar34PZzeZXwvvAePfvv6GccItRPpFMjhyMNsubeNy2WUO5BzgxtAbXR2WsANJPkSTl5ZbynOfHWB3egEAN3cK5q939ySylXV/1aqqypwvj7Jq3wWKKqotx/vFBTExIZrRPSIcErdwgIJz5p1p88+CVyvzRm9nN5l7O2551nyXiywS1qRM6jqJbZe2AbDm9BpJPpoJST5Ek1VtNPHf79P4x8aTVFab8PXUMnP0Dfy6f9vr9nZcKauilY/5l5CiKFwoKKOoopqoVt7c3SeKuxOiZX+XpibnBPzvTii+ZO7xqLhiPh7UASb8B6ITXBmdaKBBkYMI9gomtyIXbw8ZJmsuJPkQTdLRS0U8v+ogBy8UAjC4YzDzJvSwzMOoT2W1kW+OZfPpngy2ncpl07NDLeWnDevEQzfFMbB9GzQaGVNuci4fhaVjzHM6PLx+WqE0YQrc9ip4SiLZVGkUDQ92e5D5e+ezP3u/q8MRdiLJh2hSyquM/PPbU7y79SxGk4q/lwezRt/AvX1j6u3tUFWVwxeL+GxvBp8fuMSVsp8mh353Opf7+7UF4MaYVs76CMIRAqPNt9BWFEJ1hfnrcW9B1/GujkzYwfiO43lr/1scyTvC0byjdG3T1dUhiUaS5EM0GVtO5vDimsOczzdv9nV7t3DmjO9GWED9i0Kdzi5m2rL9HM8qthwLD/BiQp8oJiZEN3qhMeEmjAbY8lcoSDM/j+4LE/8Lrdq6Ni5hN0FeQYxoO4L16euZvX02S29fio/u6r2cwv1J8iHcXlZhBX/+6ihrD2UCEBHoxZxx3UjqFl6rXFW1iczCcstcjchW3mTkl+HpoSGpaxj3JMYwuGMwWhlWaR4OfgJ5pyFtG5zfbj42cBqMmA1anUtDE/Y3MX4i69PXcyz/GOvT1nN3/N2uDkk0giQfwm1VVZtYuj2NN78+RVmVEY0CUwbFMSMpHr+fbQZ35FIhn+29wOeplwj282TD9FtQFAUfTw/+MzmRbhGBBPrIL6NmZdd/YN2zPz339Ic734au41wXk3CovuF9CfQMpLCqkI+OfSTJRxMnyYdwS1tP5jDnyyOWpdH7tG3FK+O70z0qEID80io+T73Ip3sucDSzyHKeVqOQU1xJ6I9DMYM6BDs/eOE4qgpb/w6b/vLTseDOcN8yCO7ouriEwymKwoROE1hyZAmnrpwirzyPNt5tXB2WaCBJPoRbScstZe7aY3x97DIAbXw9+dPtXZiYEG25C+W9bWf5a/JxDD9uJeup1TCiaygTE6K5pVMIHlrZNaBZMplgw0z44d8/HbthHNy5CPQyf6cleLDbgyw5sgSAD499yDN9nnFxRKKhJPkQbqGw3MBb35zi/R3pGIwqWo3C5IHteGZEJ7IKK7hcXEFEoPke/05h/hiMKj2iApmYEM24XpE2L58umhhjNax+DA6v/OnYsBfh5j+ALLfdYgR7BxPfKp6TV06y5vQaST6aMJv+RJw3bx59+/bF39+f0NBQ7rzzTk6cOFGrzJQpU1AUpdZjwIABdg1aNB9V1Sb++10aQ/62ife+S8NgVBkSH8KnUwfQLtiHBxb/wG1vbmXp9nTLOYM7BpM8/Wa+fGowkwe1k8SjJdi79KfEQ+sF9y83r1gqiUeLM6X7FAByy3NJu5Lm2mBEg9mUfGzZsoUnn3ySnTt3kpKSQnV1NUlJSZSWltYqd/vtt5OZmWl5rFu3zq5Bi6bPZFL5PPUiw+dv5pWvjnKlzEDHEF9mjOyEn96D+979gZc+P8LBC4V4aBRKfrbsuVaj0CU8wIXRC6c6/TV8M8f8tW8ITN0MnUe5NCThOqPiRqHTmCeQf37mcxdHIxrKpmGX5OTkWs+XLFlCaGgoe/fu5ZZbbrEc1+v1hIeH//L0elVWVlJZWWl5XlRknjxoMBjsvltoTX2yC+n1OaqtVFVly6lc5qec5tiP62+E+Hny9LAOfPhDBvNTTlnKdgn35+4+kYztGUEbX0+3/b7JdWU9m9qqvABN6kdoNv0ZRTViihmAceL74NMGWkhby7VVvzs73Mmnpz7lRP6JOm0kbXV9jmorW+pTVFVVG/pGp0+fplOnThw6dIju3bsD5mGXNWvW4OnpSatWrRgyZAhz584lNDS03jpmz57NnDlz6hxftmwZPj6yiExzcqpQYW2GhrRic1e5TlEZEWXi1kgVvRZWpmnYm6uQEKzSP9REtKyI3WLpq/K59fj/oTeWAHA+6CYOxDyMSSO3TAvINebyZvGbKCj8MeCPBGikJ9QdlJWVMWnSJAoLCwkIuPb3pMHJh6qqjB8/noKCArZt22Y5vmLFCvz8/IiNjSUtLY0XX3yR6upq9u7di16vr1NPfT0fMTEx5ObmXjd4WxkMBlJSUhg5ciQ6nfwQuxZ7ttUPafm8tekMP6SZd53VKObb5owmlY9+m0i/dkGAedKpt06Lp0fTultFrivrWdVWOcfxWJKEYjCvZGvsOxXTyL+0yPkdcm1d3cMpD5Oak8pDXR/iqRufkraygaPaqqioiODgYKuSjwbf7TJt2jQOHjzId999V+v4vffea/m6e/fuJCYmEhsby9q1a5kwYUKdevR6fb1JiU6nc9gF5Mi6m5uGtpWqqnx3Ope3vj3NrrT8Wq+ZVEBViQ/zw2BSLPUHN/HviVxX1rtqW6Vvh/+NA9OP3be3zUM78Am0zg3P7ci1VdfgqMGk5qTyv2P/4+k+T1vaR9rKevZuK1vqalDy8dRTT/HFF1+wdetWoqOjr1k2IiKC2NhYTp06dc1yonkwmVRSjl3m7c1nOJBxpc7rAV4ejL8xinsSo+kRFVjvZnCihTr2BXwyGVQTKBq453/QdayroxJu6p74e1iYuhCjauSzU59xdwdZ8bQpsSn5UFWVp556itWrV7N582bi4uKue05eXh4ZGRlEREQ0OEjh/ioMRlbvv8Bb35zmUmEFAF46DfcmxrDpRA7tQ3yZmBDNiBvC8NK19L9jRR1734cvnwFU0HrC5K+gbX9XRyXcWJB3EDH+MWQUZ7Ds2DJJPpoYm5KPJ598kmXLlvH555/j7+9PVlYWAIGBgXh7e1NSUsLs2bO5++67iYiIID09nRdeeIHg4GDuuusuh3wA4Vr5pVX869tTLNuVQbnBaDk+9Zb2PHpLe4L99Mw0GCXhEFd3djMkzwRU8PSFx7bKUunCKhPjJ/LG3jdIK0qjpKrE1eEIG9iUfCxatAiAoUOH1jq+ZMkSpkyZglar5dChQ/zvf//jypUrREREcOutt7JixQr8/f3tFrRwvb3pBfw1+Ti70/P5+YxlvYeGsb0ieXxIB8viX5J4iKs6vApWPWae4xGVYF48zK/+O+OE+KXf3PAbFuxdgAkT/z3yXzoiSWtTYfOwy7V4e3uzYcOGRgUk3FdVtYnkI1l8sCOd3ekFtV7rHO7P1FvaM7pHhCQbwjqfTIaja8xfdx0PE/4DHnUnnwtxNZ5aT25ocwNH8o6wNn0tz+hlufWmQvZ2EfXKLKzgVKFCZmEFlwqL+EfKCU5eLqaw3LzSqFYx92iMuzGSabd2JKq1rMkirFB0ieCiI2iX/BMu7TEf6/EruOvfoJGkVdhuSrcp/HHrH8kpzyGVVBLKEogOvPaNEML1JPkQdazYfZ6Zqw5hUrUsPLq11muh/nru79eW+/u1JSxAL3erCOvt+x8eXz7DTarpp2PtboG73gFN01rbRbiP29rdxsvbX6asuozPyj9j1ZpVvDzoZSZ0qru0g3AfknwIC6PRxL82n2F+ysk6rwV4eXBPYgwzR3WRLeuF7QovwpfPoPw88UD5scdDrifRcJfLLlNeXW55bsLEnB1zGBQ5iHBf67b5EM4nyUcLp6oqxzKL+eLAJb5IvWi5TfaX3nkgkYEd2jg5OtFsZB4wr99Riwr5ZyEwyiUhiebhfNF5VGrPRzSpJjKKMyT5cGOSfLRAqqpy+GIR/9p0mq2nciir+ukWWU+tQpWx9n9kraLQLljmdIgGqiqF5D/VPa5oIai98+MRzUrbgLZoFA2mnyW3GkVDjH+MC6MS1yPJRwthMqnszyjgw53n+frYZYp/sUX9iBtCGdcriuE3hPJ56sUf53yY92F5dUJ3IgK9XRi9aLLKr8CyX8GV84AGFRUFFVXRoox9U3o9RKOF+4bz8sCXeXn7y5ZjLw98WXo93JwkH81YSWU1353KJflwJhuPXq7VwwHg5aHh5vgQ/jAyni4RP20CdG/ftgyMa80n6zbxq9G30jZY1mgRDZB9HFY+ApcPgVcg/GYV1d4h/LD+Y/qPuh9dm1hXRyiaiQmdJhDhFcFj3z4GQIh3iIsjEtcjyUczUjN/Y9upHLaczGF3ej6GXwyhaBRIiG3N1CEdGNY5FI2m/rtVIgK96BSoEhHo5YzQRXNz/gdYOhpM1eDdBiZ/DuE9wGAgz/8GCIh0dYSimUkMT8RX8aVULWXx4cXcHH2zq0MS1yDJRxOmqirn88vYcSaP78/ksf10DnmlhlplYtv4cGvnUDILyxncMYTxvSMJ8JIdH4UDnf4GProHVKN5Xsf9y82JhxAO1lXXld1VuzmQfQCTyYRG7qRyW5J8NCEmk8rJ7GJ2pxewOy2fXWn5ZBXVf3eKosCnUweS2C7IyVGKFu3Iavj0IUAFjQ4eToboRFdHJVqIYV7D2F21m2q1mi/Pfsn4juNdHZK4Ckk+3FhuSSUHL1wh9fwV9meY/y2urK5VpmbQpGZwxdNDQ1LXMO5JjKF329ZOjVe0cPs+gC+eAlTw8IJHN0FYV1dHJVoQf40/YT5hXC67zLJjyyT5cGOSfLgBVVXJKqrgWGYRRy4WcfhSIYcvFnHxSnmdsj46DX1ig0hs15rCMgNLtqcD0CumFfckRDO2ZySBPjKsIpxsx9uwYab5a50v/O47uY1WuMSo2FEsPbaUiyUXUVVVVmF2U5J8OFl+aRWns0s4ebmYU5eLOXG5mBNZxRSUGeqUVRRoH+xLlwh/VFXheGYRUwa148FB7QAoLDPgqdMwsU80ncLkjhThIlmHYfM889f6AHjyB5lQKlzm4W4P8/GJjymsKuRY/jG6tpHeN3ckyYcDFJYbOJ9Xxvn8MtLzSknLLeVsTglnc0u5Uk+SAea1NtoH+9ItMoBukYF0ifDnSlkVaw9msfHIZctdK18cuGRJPgJ9dMwcdYOzPpYQdV1KhQ/uhMoiaNMRHkoGP7nNUbiOn6cft8TcQsq5FJLTkyX5cFOSfNioqtpETkklWYUVZBVWkFlYzsUr5VwsMP+bkV9GUUX1NeuIauVNfJgfncL8iQ/zp0u4Px1D/fDSaVFVlb8mn+D3Kw6QW1JpOadHVCATE6IZ10v+ohRuQFVh3bNwYDlUlUBUAvxmFXi3cnVkQnBbu9tIOZfCl6e/ZGqPqfh6+ro6JPELLT75MJpUiisMFJQZKCiroqC0irzSKvJ/fOQWV5JTUklOsfmRV1plVb3BfnraBnnTLtiXdm18iQv2pX2IL+2D/fD2rL11eGllNV468zFFUTh5uZjckkqC/Ty588YoJiZG0yU8oL63EcL5TCb4dDIc+8L8PCoRHlgNXnKNCvdwc9TNKCjkVuTy4bEPmdprqqtDEr/QYpKPsqpqnlq2n3OXtPw7bQfFldUUlhsoqaxGVa9//s/ptAqh/l6EB3oR2cqbyEAvolp7E93am6hWPsQEeePjee2mrTaa2HY6l8/2XODrY5f55g9DiG5t3j/lyVs7cH+/tgztHIJOdpAV7sRoMK/hcXaT+Xnr9vDgGtDLnCPhPnx0PsQFxnG28CxrTq+R5MMNtZjkQ6fV8M3xHECBouI6r/t6amnl40mQryetfT1p8+Mj2F9PsJ+eEH89IX56QgP0BPl4XnVl0Os5nV3CZ3svsHr/BS4X/TSssul4Ng8MbAdAQqyszSHcUFUZfDAeMnaZn4d0gUe/BenSFm7o7k5387c9f+NCyQVyy3IJ9gl2dUjiZ1pU8jF3fFdOHj3EzQMSCfL3JsBLR6C3+eHp4dgehrM5Jfzh0wPsP3/Fcqy1j47xN0ZxT2I03SIDHfr+QjRKRSEsGQ2XD5ufh3WH36aAp+x2LNzTxPiJ/H3P31FR+fDYh0xPmO7qkMTPtJjkA+BXidGsyz7IkPgQdDrHroVhNKlkF1dYdoMNC/DiRFYxWo3CrZ1DmJgQzbAuYQ5PeoSwi5WP/JR4RNwID62XxEO4NR+dDx1adeD0ldN8efZLST7cTItKPpwhLbeUlXsvsHLfBQK9dax/5mYURcFX78Hbv+5D18gAQv1lszbRhKR/B2nbzF9HJcKUr0Dn7dqYhLDCPfH3MG/XPLLLsskoziDGP8bVIYkfyZ/ddlBSWc2K3ee559/bufXvm1m46TSZhRVculJea17H0M6hkniIpqP8ijnp+OgeqC6HDsMl8RBNyh0d7kD5cROKVadWuTga8XPS89FIH+xI59V1xyk3GAHzlvW3xJuHVUbcEGa5hVaIJiXzALw/DqpKwWSAjiPg3o9AJ8mzaDoCPAPoEdKDgzkH8dZK0uxOJPmwUUZ+GXoPDaEB5h/C0a19KDcYaR/iyz0JMdzVO4rwQPkBLZqwc9vhw7vBUGZ+3mG4JB6iybqr410czDnINxnf8Fivx1wdjviRJB9WKK2sZv3hLD7dk8EPafn8bmgH/nR7FwBu7hTMqicG0TumlWxgJJq+UymwfBIYf1xML24o3LdMEg/RZN0acyuv7HiFo3lHuVR8iUh/WSXaHUjycRWqqrIrLZ/P9l5g7aFMyqrMwyqKApeLKizlPLQa+sjW9aI5OLwSVj4Kqvlap8NwSTxEk9fGuw09gntwMPcgk9ZN4pt7vkGrkeFwV5Pkox6qqnLnv77nwIVCy7F2bXyYmBDNhD7RRLaSsUPRzOxZAl/9HvhxuV+Z4yGakRFtR3Aw9yB5FXnsvrybAREDXB1Siyd3uwDlVUbWHcpE/XGddUVR6BXTCl9PLfcmxvDp4wPZ9OxQpg3rJImHaJ4u7eOnxGOkJB6iWUmKS7J8vfrUahdGImq02J4PVVXZd76AT/dc4KuDmZRUVvPp4wPp2868tPkzwzvx/Kgu192jRYgmL20bHPjE/HWHEXDvh5J4iGYlyi+Ktv5tOV98nm/Of0OlsRK9Vu/qsFq0Fveb9UolLNpyltWpmaTlllqOxwR5U1hmsDxv4ycXpmjGTEbY/k8I7QqfTAZjxY89HpJ4iOZpdNxo/n3w31QaK9mSsYWkdknXP0k4TItKPo5mFjF7nxaV0wB467SM7hHBPYnR9GsX1ODN4oRoUqqrYNWjcHQNKBpQTZJ4iGZvWNth/PvgvwH48uyXkny4WItKPrqE+ROkh/YRrbknMYbRPSLw07eoJhAtXVUprHgAznxjfi6Jh2ghugR1Idg7mNzyXL678B2FlYUE6mVDT1dpUb95NRqF53oZmTC2r8M3lhPC7ZRfgWX3QsbOn451lDkeomVQFIWRsSP5+PjHdGzd0XKDgXCNFne3i5fc3i1aopJsWHpHPYmH3NUiWo5bY24FIKcshwB9gIujadlaXPIhRIujquZJpZcP/XRMEg/RAiWGJeKn8yOvIo/DuYddHU6LZlPyMW/ePPr27Yu/vz+hoaHceeednDhxolYZVVWZPXs2kZGReHt7M3ToUI4cOWLXoIUQNlAU6HU//Li7pyQeoqXSaXXcFHUTAEsOL2HT+U0ujqjlsin52LJlC08++SQ7d+4kJSWF6upqkpKSKC396ZbV119/nfnz57Nw4UJ2795NeHg4I0eOpLi42O7BCyGuoerHjeHStsL65wBVFhATLd6Q6CEAfH3+a94+8LaLo2m5bJpwmpycXOv5kiVLCA0NZe/evdxyyy2oqsqbb77JrFmzmDBhAgDvv/8+YWFhLFu2jKlTp9aps7KyksrKSsvzoqIiAAwGAwaDoU75xqipz971NkfSVtZzx7ZSzn2HdvVjGAc9jXbTXJTqckwdRmC8ewmgBRfF6o5t5c6kvaxnbVsNDBuIBg0mTBzPP86J3BO0D2zvjBDdhqOuK1vqU9RGTPk9ffo0nTp14tChQ3Tv3p2zZ8/SoUMH9u3bR+/evS3lxo8fT6tWrXj//ffr1DF79mzmzJlT5/iyZcvw8fFpaGhCtFhhhfvpm7YQrWrAhIIGlcsBPdkV9zQmjaerwxPC5d4rfo90YzoAQ/RDGOk90rUBNRNlZWVMmjSJwsJCAgKuPaG3wcmHqqqMHz+egoICtm3bBsD27du56aabuHjxIpGRP21b/Nhjj3Hu3Dk2bNhQp576ej5iYmLIzc29bvC2MhgMpKSkMHLkSLnV9jqkraznTm2lHP4U7RfTUFQjqqJBUU3mHo+J74OH61ftdae2agqkvaxnS1stPbqUf6b+E4BI30i+HPclitJyFpl01HVVVFREcHCwVclHg9f5mDZtGgcPHuS7776r89ovv4mqql71G6vX69Hr6/5Q1Ol0DvvP5si6mxtpK+u5vK12/QfWPWv++sfEg063obn3AzRukHj8nMvbqomR9rKeNW01LHaYJfm4VHqJI1eO0Du09zXPaY7sfV3ZUleDbrV96qmn+OKLL9i0aRPR0dGW4+Hh4QBkZWXVKp+dnU1YWFhD3koIcT2qClv+9rPEQ2teuTT+drj3A7fo8RDCnbQPbE+UX5Tl+dqza10YTctkU/KhqirTpk1j1apVfPvtt8TFxdV6PS4ujvDwcFJSUizHqqqq2LJlC4MGDbJPxEKI2lQVsg6av1a0oBqh82j41f8k8RCiHoqiWO56AbhQfMGF0bRMNiUfTz75JB9++CHLli3D39+frKwssrKyKC8vB8zf0OnTp/Pqq6+yevVqDh8+zJQpU/Dx8WHSpEkO+QBCtHgaDfS8FzQe5sSjyx1wj3vM8RDCXd0SfQsAQfogFo1Y5OJoWh6b5nwsWmT+Bg0dOrTW8SVLljBlyhQAnnvuOcrLy3niiScoKCigf//+bNy4EX9/f7sELIQAqith/weQ8DCcTIZPp4CpGm4YCxOXgFbmBwhxLYnhiXh7eJNfmc/JgpN0Durs6pBaFJuSD2tujFEUhdmzZzN79uyGxiSEuJbKEljxGzi7CU5/A6c2mhOPbnfBhP9I4iGEFfRaPf3D+7P5wma2XthKpF8knlpP9FrpMXQG2dtFiKakLB8+uNOceGj1cCLZnHh0nwgT3pPEQwgb3Bx9MwDLjy9n6IqhpJxLuc4Zwl4k+RCiqSjOgqVj4MJu0PmAsQowQc/7YMK7oG3wnfNCtEiDowYDkF2eTZWpSu56cSJJPoRoCgrS4b+3QfZR0AeCoQxQofdv4M63QaN1dYRCNDmRfpF0bNXR8nzHpR3klee5MKKWQ5IPIdxddSW8P9acgPi0gcpC8/GEh2DsW5J4CNEINb0frfStMKpGNqTXXYlb2J8kH0K4Ow89jPwz+EdA2Y9/lfV/HO54w3ybrRCiwWqSjypjFQBr02ToxRnkJ5cQ7sr4sx0iC9KhONP89aCn4fbXoAXtRSGEo/QJ7YOPhw9l1WUoKBzMOUhGcYarw2r2JPkQwh0d+wreHgBXMmDza/D1y+bjt/wRRr4iiYcQdqLT6ugf0R+AaH/zdiHrzq5zZUgtgkyPF8LdpC6Dz58078/yyQNwab/5+LAX4ZZnXRubEM3Q4KjBbMrYhKfGkz8k/IFRcaNcHVKzJ8mHEO5k5yJIft78dXD8T4nHbfNg4BOui0uIZuymqJsASC9K5+74u/H3lBW5HU2GXYRwB6oKm+b9lHiEdIHck4ACd7wpiYcQDhTlF0W7gHYYVSM/ZP7g6nBaBEk+hHA1kwnW/wm2vGZ+HnID5Bw371B71zuQ+JBr4xOiBajp/dh6YSufn/6cP275I0aT0cVRNV+SfAjhalUlkL7N/HVwZ8g5Bhod/Op96HWva2MTooUYFDkIgJ2XdvL67tdJTk9m9+XdLo6q+ZLkQwhX8wqAX/3PnHjkngAPb5i03LxDrRDCKRLDEtFpdGSWZTIwciCALLfuQJJ8COEKlcVw7Evz16V5sOpRc+KhD4AHVkHHEa6NT4gWxkfnQ5+wPgC08WoDwNfnvqbSWOnKsJotST6EcLayfHh/HKz4Dez8NywZZb6rxacNTP4SYge5OkIhWqSaoZcLxRcI9w2nxFDClowtLo6qeZLkQwhnKrr0Y7KxD7wCYdt8c49HQBQ8lAyRN7o6QiFarJrkY/fl3dze7nZAhl4cRZIPIZwl74x5Z9qc4+AbAooGSi9Dm47wcDKExLs6QiFatPjW8QR5BVFeXU5cYBwA2y5uo7BmM0dhN5J8COEMWYfhv7fDlfPmDeKqyqC8AMJ7mns8WrV1dYRCtHgaRWOZbHqh+ALxreO5MfRG8iryXBxZ8yMrnArhaEWZsHQ0VBSak4yiTDAZIHYw3P+x+W4XIYRbGBgxkLVn17L90naWjVmGXqt3dUjNkvR8COFoARGQ+DC0bmfeKM5kgC53wG9WSuIhhJsZEDEAgKN5R6mornBxNM2XJB9COIrJZP5XVUHrBQXpgAp9HoR73gedlyujE0LUI8w3jA6BHVBRLUut55bncjTvqIsja14k+RDCEfZ9AB+Mh8oSWDsDtswzH7/5WRj7T9DKiKcQ7qpm3sfOzJ1sydjCiE9H8PL2l10cVfMiyYcQ9rb9LfhiGqRthcW3wZ7/AgqM/jsMfxEUxdURCiGuoWboZcelHfQK6YWCwvH845y5csbFkTUfknwIYS+qCt/8GTb+n/m5fwRkHwat3rxPS79HXRufEMIqieGJeCgeXCi5QLGhmMFRgwFZ88OeJPkQwh5UE5oNf4Jtfzc/92kDxZnmhcQeWA1dx7s2PiGE1Xx1vvQM6QmYh17GtB8DwLq0daiq6srQmg1JPoRoLKOBPufeQbv3x+EVTz8oy4PAGHh4I7S7ydURCiFsVDP08kPmDwyJGYKPhw8XSy6SmpPq2sCaCUk+hGisoguEFR1EVbSg8YCqEgjvAb9NgdAuro5OCNEA/SP6A7Arcxd6rZ4RsebNHmXoxT4k+RCisVrHcT5oMKhG8xoeHUfAQ+vN63sIIZqkHsE98PbwpqCygFMFpxgdNxqAb89/i0k1uTi6pk+SDyEaw2REs2EmHXM2oAAkTIH7V4De38WBCSEaQ6fVkRCWAJjnffSP6M+cQXNYPX41GkV+dTaWtKAQjaGqKFfSATAOexnueFPW8BCimfj5vA8PjQcTOk0gUB/o4qiaB0k+hGgMrQfGu/7DjvZ/wDTwKVnDQ4hmpGbex97LezGYDLVek7teGkeSDyEay9OP7MBero5CCGFn8a3jCdQHUlZdxpHcIwCsT1vPr9f9mrVpMvG0MST5EEIIIeqhUTT0C+8HwK6sXQCkFaZxMOeg3PXSSJJ8CCGEEFdhST4yzclHzYJjOy7tIK88z2VxNXWSfAghhBBX0S/CnHzsz95PpbGS2IBYurfpjlE1siF9g4uja7psTj62bt3K2LFjiYyMRFEU1qxZU+v1KVOmoChKrceAAQPsFa8QQgjhNHEBcYR4h1BlquJA9gHgp94PmffRcDYnH6WlpfTq1YuFCxdetcztt99OZmam5bFu3bpGBSmEEEK4gqIo9A3vC/w07+P2uNvRKBoO5hwkoyjDleE1WTYvSDBq1ChGjRp1zTJ6vZ7w8PAGByWEEEK4i37h/ViXto7dWbsBCPYOpn94f3Zk7mBt2loe7/W4iyNsehyyGtLmzZsJDQ2lVatWDBkyhLlz5xIaGlpv2crKSiorKy3Pi4qKADAYDBgMhnrPaaia+uxdb3MkbWU9aSvrSVvZRtrLeo5sqxuDbwTgYO5BisqL8Pbw5o64O9BpdHRp1aXJfX8c1Va21KeojVgpRVEUVq9ezZ133mk5tmLFCvz8/IiNjSUtLY0XX3yR6upq9u7di16vr1PH7NmzmTNnTp3jy5Ytw8fHp6GhCSGEEHahqip/K/obRWoRU3yn0FHX0dUhuaWysjImTZpEYWEhAQEB1yxr9+TjlzIzM4mNjWX58uVMmDChzuv19XzExMSQm5t73eBtZTAYSElJYeTIkeh0OrvW3dxIW1lP2sp60la2kfaynqPb6sXtL7I2fS2/7fZbnuz1pN3rdyZHtVVRURHBwcFWJR8O34QiIiKC2NhYTp06Ve/rer2+3h4RnU7nsP9sjqy7uZG2sp60lfWkrWwj7WU9R7VV/8j+rE1fy97svbXqv1B8ga/Pfc0DXR9Aq9Ha/X0dyd5tZUtdDk8+8vLyyMjIICJCthcXQgjRNNXc8XI49zBlhjJ8dD5Um6q5b+19FFYW0qVNF8tGdOL6bL7VtqSkhNTUVFJTUwFIS0sjNTWV8+fPU1JSwrPPPsuOHTtIT09n8+bNjB07luDgYO666y57xy6EEEI4RZRfFBG+EVSr1RzIMa/34aHxYGTsSABZbt1GNicfe/bsoXfv3vTu3RuAGTNm0Lt3b1566SW0Wi2HDh1i/PjxxMfHM3nyZOLj49mxYwf+/v52D14IIYRwBkVRSAxLBLDccgswJs684NjX576m0lhZ77miLpuHXYYOHXrNrYQ3bJDlZoUQQjQ/ieGJfHn2S/Ze3ms51iesD+G+4WSVZrElYwtJ7ZJcGGHTIXu7CCGEEFboG2ae93Ew9yDl1eWAeefb0XGjARl6sYUkH0IIIYQVov2jCfUJpdr007wP+Gmvl20Xt1FYWeiq8JoUST6EEEIIK/x83sfPh17iW8fTsVVHPDQenMg/4arwmhSH32orhBBCNBeJ4YmsS1tXK/kA+MeQfxDuG46PTlbmtoYkH0IIIYSVEsISADiYc5AqYxWeWk8A2rdq78qwmhwZdhFCCCGsFBcQR5BXEJXGSg7nHq7zuqqqMu/DCpJ8CCGEEFZSFMXS+/HLoZdjeceY8MUEHtn4iCtCa1Ik+RBCCCFsUJN87Lm8p9bxCN8I0gvTOZ5/nDNXzrgitCZDkg8hhBDCBjV3vOzP3k+1qdpyvJVXKwZHDQZkzY/rkeRDCCGEsEHHVh3x9/SnvLq8zq21NWt+rEtbd83VwFs6ST6EEEIIG2g1WnqHmvc3++W8jyExQ/Dx8OFiyUVSc1JdEF3TIMmHEEIIYaM+oX2AusmHt4c3I2JHADL0ci2SfAghhBA2qpl0uj97f53hlZq9Xjakb8BgMjg9tqZAFhkTQgghbNStTTf0Wj0FlQWkFabVWmSsf0R/JsZP5NaYW9HI3/j1klYRQgghbKTT6ugZ0hOAvdm1h148NB68PPBlbom+Ba1G64rw3J4kH0IIIUQD1Mz72H95v4sjaXok+RBCCCEaoCb52Je9r97Xz145yxt732DT+U3ODKtJkORDCCGEaICeIT3RKBoullzkcunlOq8npyfz38P/ZcXJFS6Izr1J8iGEEEI0gJ+nH51bdwbMd738Us2CYzsv7SSvPM+psbk7ST6EEEKIBqpZbKy+oZfYgFi6t+mOUTWyIX2Ds0Nza5J8CCGEEA3UO+zH5ONy/fM+ano/1qbJgmM/J8mHEEII0UA1k05PXTlFSVVJnddvj7sdjaLhYM5BMooynB2e25LkQwghhGigUJ9QovyiMKkmDuYcrPN6sHcwAyIGANL78XOSfAghhBCNcGPojQDsz6l/vY/RcaNppW+Fh0YWFa8hLSGEEEI0Qu+Q3qw9u7beO14ARsWNYnTcaHRanZMjc1+SfAghhBCNUDPp9GDOQapN1XV6ODy1nq4Iy63JsIsQQgjRCB1bdcRf5095dTknC05etZxJNbE/ez9Gk9GJ0bknST6EEEKIRtAoGnqGmjeZu9rQi6qq3PfVfTy4/kF2Ze1yZnhuSZIPIYQQopF6h5iHXg5kH6j3dUVR6BbcDYC1Z+WuF0k+hBBCiEaqueMlNSf1qmXGxJkXHPv6/NdUVFc4ISr3JcmHEEII0Ug9gnugUTRklmaSVZpVb5k+YX0I9w2n1FDK1gtbnRyhe5HkQwghhGgkH52PZZO5Azn1D71oFA2j40YDMvQiyYcQQghhB71CegGQmp161TI1e71su7iNwspCZ4TlliT5EEIIIeygZt7H1Xo+AOJbx9OpdScMJgObMzY7JS53JIuMCSGEEHZQk3wcyztGRXUFXh5e9ZZ7NuFZ9B56eof2dmJ07sXmno+tW7cyduxYIiMjURSFNWvW1HpdVVVmz55NZGQk3t7eDB06lCNHjtgrXiGEEMItRfpGEuwdTLVazZG8q//eGxQ1iISwBDRKyx18sPmTl5aW0qtXLxYuXFjv66+//jrz589n4cKF7N69m/DwcEaOHElxcXGjgxVCCCHclaIolnkf1xp6EQ1IPkaNGsVf/vIXJkyYUOc1VVV58803mTVrFhMmTKB79+68//77lJWVsWzZMrsELIQQQrgrS/JxlcXGauSU5fCXnX/h0Y2POiMst2PXOR9paWlkZWWRlJRkOabX6xkyZAjbt29n6tSpdc6prKyksrLS8ryoqAgAg8GAwWCwZ3iW+uxdb3MkbWU9aSvrSVvZRtrLeu7SVt1am1cxPZBzgKqqKhRFqb+gCVaeXEm1Ws3xnON0aNXBaTE6qq1sqc+uyUdWlnlhlbCwsFrHw8LCOHfuXL3nzJs3jzlz5tQ5vnHjRnx8fOwZnkVKSopD6m2OpK2sJ21lPWkr20h7Wc/VbWVQDWjQkFeRx0dffUSQNuiqZTtqO3K8+jhvffMWSd5JVy3nKPZuq7KyMqvLOuRul19meqqqXjX7mzlzJjNmzLA8LyoqIiYmhqSkJAICAuwal8FgICUlhZEjR6LT6exad3MjbWU9aSvrSVvZRtrLeu7UVis3rORw3mGCewRze7vbr1pOe07LzO9ncsrjFG+MeuPqvSR25qi2qhm5sIZdk4/w8HDA3AMSERFhOZ6dnV2nN6SGXq9Hr9fXOa7T6Rx2ATmy7uZG2sp60lbWk7ayjbSX9dyhrW4MvZHDeYc5nH+YsZ3GXrXc8HbD8fnBh8zSTI5cOeL0W2/t3Va21GXX+3zi4uIIDw+v1ZVTVVXFli1bGDRokD3fSgghhHBLPUN6AnAw5+A1y3l7eDMidgTQ8pZbtzn5KCkpITU1ldTUVMA8yTQ1NZXz58+jKArTp0/n1VdfZfXq1Rw+fJgpU6bg4+PDpEmT7B27EEII4XZqko/j+cevu3ttzU63G9I3YDC1nInFNg+77Nmzh1tvvdXyvGa+xuTJk1m6dCnPPfcc5eXlPPHEExQUFNC/f382btyIv7+//aIWQggh3FSkbyRtvNqQV5HH8fzjlpVP69Mvoh/d23Snb0RfKqor0Hm2jOE1m5OPoUOHoqrqVV9XFIXZs2cze/bsxsQlhBBCNEmKotAzpCebMjZxIOfANZMPD40HH9/xsfOCcxMtd21XIYQQwkFqFhu73ryPlkqSDyGEEMLOauZ9WLvMerWpmm0XtrHv8j5HhuU2JPkQQggh7Kxbm25oFA2Xyy5zufTydcsvObyEJ755gncPveuE6FxPkg8hhBDCznx0PnRq1QmAQ7mHrls+qZ15hdOdl3aSV57n0NjcgSQfQgghhAP0COkBwMHc68/7iA2IpXub7hhVI8npyY4OzeUk+RBCCCEcoGewed7HoZzr93wAjGlvXvNjXdo6h8XkLiT5EEIIIRygZtLpkbwjVJuqr1v+9rjb0SgaDuYcJKMow9HhuZQkH0IIIYQDxAXG4afzo7y6nDNXzly3fLB3MAMiBgCwNq15L7cuyYcQQgjhABpFQ7fgboB18z7gp6GXI3lHHBaXO5DkQwghhHAQW+d9jGg7gk/Hfso/b/2nI8NyOZuXVxdCCCGEdXoEm+94seZ2WzDfotslqIsjQ3IL0vMhhBBCOEj34O4AnLlyhlJDqU3nlleXYzQZHRGWy0nyIYQQQjhIiE8I4b7hqKgczTtq9Xmv7XqNISuGsCtrlwOjcx1JPoQQQggHsnXoBaDKWEV5dTlrzzbPu14k+RBCCCEcqCb5OJx72Opzau56+fr811RUVzgkLleS5EMIIYRwoJp5HwdzrLvdFqB3aG/CfcMpNZSy9cJWR4XmMpJ8CCGEEA708x1uc8pyrDpHo2gYHTcaoFkOvUjyIYQQQjiQj86H9oHtgYYNvWy7uI3CykKHxOYqknwIIYQQDlYz9GLLpNP41vF0at0Jg8lAyrkUR4XmErLImBBCCOFgPYJ7sOb0GpuXTX+w64NcLr3MoMhBDorMNST5EEIIIRysZo+Xw7mHUVUVRVGsOu/Ojnc6MCrXkWEXIYQQwsHiW8XjqfGkqKqIjOIMV4fjcpJ8CCGEEA6m0+ose7bYMukUoNJYSXJ6Mn/d9VdHhOYSknwIIYQQTtCQSacAFdUVzNw2kw+PfcjpgtOOCM3pJPkQQgghnKAm+bB10mmgPpDBUYMBWJvWPNb8kORDCCGEcIJubcyTTo/nH6faVG3TuTVrfqw7uw6TarJ7bM4myYcQQgjhBO0C2+Hj4UN5dTlnC8/adO6Q6CH4ePhwqfQSB3IOOChC55HkQwghhHACjaKha5uuABzJtW3oxdvDmxGxI4Dmsdy6JB9CCCGEkzR03gfAmDjz0MuG9A0YTAa7xuVsknwIIYQQTlIz78PW220B+kX0I9g7mLb+ba3eoM5dyQqnQgghhJPUrHR6ouAEVcYqPLWeVp/rofHg8zs/J8AzwFHhOY30fAghhBBOEu0XTaA+kGpTNaeunLL5/OaQeIAkH0IIIYTTKIpC16CGTTr9ucLKQs4XnbdXWE4nyYcQQgjhRDVDL0fzjjbo/PVp6xn6yVBe3fWqPcNyKkk+hBBCCCeqmXTa0OSjW5tuVJuq2XlpJ3nlefYMzWnsnnzMnj0bRVFqPcLDw+39NkIIIUSTVJN8nCo4RaWx0ubz2wa0pUdwD4yqkeT0ZHuH5xQO6fno1q0bmZmZlsehQ7ZtoiOEEEI0V+G+4QR5BVGtVnMy/2SD6vj5cutNkUOSDw8PD8LDwy2PkJAQR7yNEEII0eQoimJZ6bShQy+3tbsNjaLhYO5BMooy7BmeUzhknY9Tp04RGRmJXq+nf//+vPrqq7Rv377espWVlVRW/tTtVFRUBIDBYMBgsO8KbjX12bve5kjaynrSVtaTtrKNtJf1mlpbdWnVhe8ufsehnENM6DDB5vMDPQLpF9aPnVk7+fL0lzza41Grz3VUW9lSn6KqqmrPN1+/fj1lZWXEx8dz+fJl/vKXv3D8+HGOHDlCmzZt6pSfPXs2c+bMqXN82bJl+Pj42DM0IYQQwi0crTrKsrJlhGvCmRYwrUF17K/az8qylYRqQnk64Gk7R2i7srIyJk2aRGFhIQEB116PxO7Jxy+VlpbSoUMHnnvuOWbMmFHn9fp6PmJiYsjNzb1u8LYyGAykpKQwcuRIdDqdXetubqStrCdtZT1pK9tIe1mvqbVVVmkWoz8fjYfiwbZfbUOv1dtcR6mhlM/PfE5SbBLB3sFWn+eotioqKiI4ONiq5MPhy6v7+vrSo0cPTp2qfyU3vV6PXl+30XU6ncMuIEfW3dxIW1lP2sp60la2kfayXlNpq+jAaIK8gsivyCetOI0eIT1srqOVrhWTe0xucAz2bitb6nL4Oh+VlZUcO3aMiIgIR7+VEEII0SQoisINbW4AGj7ptCmze/Lx7LPPsmXLFtLS0vjhhx+YOHEiRUVFTJ7c8OxMCCGEaG5qllk/mt+45GN92np+u+G37MzcaY+wnMLuwy4XLlzg/vvvJzc3l5CQEAYMGMDOnTuJjY2191sJIYQQTVZjVzqtsTtrN7uydhHhG8GAiAH2CM3h7J58LF++3N5VCiGEEM1OzVofpwtOU2msbNCkUzAvOPbpyU/5+vzX/F/1/+Hl4WXPMB1C9nYRQgghXCDcN5zW+tZUq9WcKqj/pgxr9A7tTYRvBKWGUrZe2GrHCB1Hkg8hhBDCBew16VSjaBgVNwqAtWfX2iU2R5PkQwghhHCRmqGXY/nHGlVPzV4v2y5uo7CysNFxOZokH0IIIYSL3BBk7vk4lte45CO+dTydWnfCYDLw9bmv7RGaQ0nyIYQQQrhIzbDLyYKTGIyN22tlXPtxDIgYQLhvuD1CcyiHr3AqhBBCiPpF+0Xj7+lPcVUxZwrP0CWoS4PrmtxtMlO6T7FfcA4kPR9CCCGEiyiKYllsrLFDL4qi2CMkp5DkQwghhHChmqGXI3lH7FJfdlk2q0+ttktdjiLDLkIIIYQL1Uw6PZ5/vNF1lRnKGL1qNJXGSnoE96Bj646NrtMRpOdDCCGEcKEubczzPE4WnMRoMjaqLh+dDwMjBwKwNs191/yQ5EMIIYRwoVj/WLw9vCmvLudc0blG11ez5se6s+swqaZG1+cIknwIIYQQLqTVaOncujPQ+B1uAYZGD8XHw4dLpZdIzU5tdH2OIMmHEEII4WI1k06P5zV+3oeXhxcjYkcA7rvcuiQfQgghhItZVjpt5DLrNcbEmYdeNpzb0OjFyxxBkg8hhBDCxWoWFzuWfwxVVRtdX7+IfrTxakO5oZyTBScbXZ+9ya22QgghhIt1bNURD40HxVXFXCy5SLR/dKPq89B48M9h/yQuMA5/T387RWk/0vMhhBBCuJhOq6NTq06Afdb7AOgZ0tMtEw+Q5EMIIYRwCzVDL/ZKPn6uorrC7nU2hiQfQgghhBvoHGS+3daeyceBnAPc99V9TN883W512oPM+RBCCCHcgL3veAForW/NkbwjaBUteeV5tPFuY7e6G0N6PoQQQgg30DmoMwoK2WXZ5Ffk26XOtgFt6RHcA6NqJDk92S512oMkH0IIIYQb8NX50jagLWDfoZefL7fuLiT5EEIIIdyEIyad3tbuNjSKhoO5BzlfdN5u9TaGJB9CCCGEm7AkH3ZYZr1GsHcwAyIGAO6z060kH0IIIYSbsCQfBfa93fbnQy/2WEG1seRuFyGEEMJN1CQf6YXplBnK8NH52KXe4W2HsyV2C7fH3Y6KJB9CCCGE+FGwdzBtvNqQV5HH6Sun6RnS0y71+up8+cfQfwBgMLh+ozkZdhFCCCHcSE3vx4mCEy6OxHEk+RBCCCHcSM1Kpyfy7Z98nC86zzuH3uF8tWvvepHkQwghhHAjjtzjZemRpbxz6B12V+22e922kORDCCGEcCM1PR8nC05iNBntWveY9mPo3Loz0dpou9ZrK0k+hBBCCDcS6x+Ll9aL8upyzhfbd3ikT2gfPh71Mf31/e1ar60k+RBCCCHciFajpVPrToD9J50qimLX+hpKkg8hhBDCzViGXvJPujgSx5DkQwghhHAznVubkw9HTDp1B5J8CCGEEG7GcrttM13rw2HJx9tvv01cXBxeXl4kJCSwbds2R72VEEII0azEt44HILssm4KKAhdHY38OST5WrFjB9OnTmTVrFvv37+fmm29m1KhRnD/vHlv5CiGEEO7MV+dLjH8M0Dx7Pxyyt8v8+fP57W9/yyOPPALAm2++yYYNG1i0aBHz5s2rVbayspLKykrL88LCQgDy8/Ptvv68wWCgrKyMvLw8dDqdXetubqStrCdtZT1pK9tIe1mvObZVrC6W9PJ09qXto5NnJ7vV66i2Ki4uBrBu11zVziorK1WtVquuWrWq1vGnn35aveWWW+qUf/nll1VAHvKQhzzkIQ95NINHRkbGdXMFu/d85ObmYjQaCQsLq3U8LCyMrKysOuVnzpzJjBkzLM9NJhP5+fm0adPG7vcjFxUVERMTQ0ZGBgEBAXatu7mRtrKetJX1pK1sI+1lPWkr6zmqrVRVpbi4mMjIyOuWdciwC9RdyERV1XqTCb1ej16vr3WsVatWjgoLgICAALk4rSRtZT1pK+tJW9lG2st60lbWc0RbBQYGWlXO7hNOg4OD0Wq1dXo5srOz6/SGCCGEEKLlsXvy4enpSUJCAikpKbWOp6SkMGjQIHu/nRBCCCGaGIcMu8yYMYMHHniAxMREBg4cyLvvvsv58+d5/PHHHfF2VtPr9bz88st1hnlEXdJW1pO2sp60lW2kvawnbWU9d2grRVWtuSfGdm+//Tavv/46mZmZdO/enTfeeINbbrnFEW8lhBBCiCbEYcmHEEIIIUR9ZG8XIYQQQjiVJB9CCCGEcCpJPoQQQgjhVJJ8CCGEEMKpml3y8fbbbxMXF4eXlxcJCQls27btqmU3b96Moih1HsePH3dixK6xdetWxo4dS2RkJIqisGbNmuues2XLFhISEvDy8qJ9+/b8+9//dnygbsDWtmqp19W8efPo27cv/v7+hIaGcuedd3LixPV342yp11VD2qulXluLFi2iZ8+elhU5Bw4cyPr16695Tku9rmxtK1ddU80q+VixYgXTp09n1qxZ7N+/n5tvvplRo0Zx/vz5a5534sQJMjMzLY9Oney3e6C7Ki0tpVevXixcuNCq8mlpaYwePZqbb76Z/fv388ILL/D000+zcuVKB0fqera2VY2Wdl1t2bKFJ598kp07d5KSkkJ1dTVJSUmUlpZe9ZyWfF01pL1qtLRrKzo6mtdee409e/awZ88ehg0bxvjx4zly5Ei95VvydWVrW9Vw+jVlh41s3Ua/fv3Uxx9/vNaxLl26qM8//3y95Tdt2qQCakFBgROic1+Aunr16muWee6559QuXbrUOjZ16lR1wIABDozM/VjTVnJdmWVnZ6uAumXLlquWkevqJ9a0l1xbP2ndurX63nvv1fuaXFe1XautXHVNNZuej6qqKvbu3UtSUlKt40lJSWzfvv2a5/bu3ZuIiAiGDx/Opk2bHBlmk7Vjx446bXvbbbexZ88eDAaDi6Jyby39uiosLAQgKCjoqmXkuvqJNe1VoyVfW0ajkeXLl1NaWsrAgQPrLSPXlZk1bVXD2ddUs0k+cnNzMRqNdTavCwsLq7PJXY2IiAjeffddVq5cyapVq+jcuTPDhw9n69atzgi5ScnKyqq3baurq8nNzXVRVO5JrivzLtYzZsxg8ODBdO/e/arl5Loys7a9WvK1dejQIfz8/NDr9Tz++OOsXr2arl271lu2pV9XtrSVq64ph+zt4kqKotR6rqpqnWM1OnfuTOfOnS3PBw4cSEZGBn//+99lKfh61Ne29R1v6eS6gmnTpnHw4EG+++6765aV68r69mrJ11bnzp1JTU3lypUrrFy5ksmTJ7Nly5ar/lJtydeVLW3lqmuq2fR8BAcHo9Vq6/RyZGdn18mAr2XAgAGcOnXK3uE1eeHh4fW2rYeHB23atHFRVE1HS7qunnrqKb744gs2bdpEdHT0NcvKdWVbe9WnpVxbnp6edOzYkcTERObNm0evXr1YsGBBvWVb+nVlS1vVxxnXVLNJPjw9PUlISCAlJaXW8ZSUFAYNGmR1Pfv37yciIsLe4TV5AwcOrNO2GzduJDExEZ1O56Komo6WcF2pqsq0adNYtWoV3377LXFxcdc9pyVfVw1pr/q0hGurPqqqUllZWe9rLfm6qs+12qo+TrmmnDq91cGWL1+u6nQ6dfHixerRo0fV6dOnq76+vmp6erqqqqr6/PPPqw888ICl/BtvvKGuXr1aPXnypHr48GH1+eefVwF15cqVrvoITlNcXKzu379f3b9/vwqo8+fPV/fv36+eO3dOVdW6bXX27FnVx8dH/f3vf68ePXpUXbx4sarT6dTPPvvMVR/BaWxtq5Z6Xf3ud79TAwMD1c2bN6uZmZmWR1lZmaWMXFc/aUh7tdRra+bMmerWrVvVtLQ09eDBg+oLL7ygajQadePGjaqqynX1c7a2lauuqWaVfKiqqv7rX/9SY2NjVU9PT7VPnz61blubPHmyOmTIEMvzv/71r2qHDh1ULy8vtXXr1urgwYPVtWvXuiBq56u5veqXj8mTJ6uqWretVFVVN2/erPbu3Vv19PRU27Vrpy5atMj5gbuArW3VUq+r+toIUJcsWWIpI9fVTxrSXi312nr44YctP9dDQkLU4cOHW36ZqqpcVz9na1u56ppSVPXHWThCCCGEEE7QbOZ8CCGEEKJpkORDCCGEEE4lyYcQQgghnEqSDyGEEEI4lSQfQgghhHAqST6EEEII4VSSfAghhBDCqST5EEIIIYRTSfIhhBBCCKeS5EMIIYQQTiXJhxBCCCGc6v8Bf1dD/ZpJNzwAAAAASUVORK5CYII=\n",
                        "text/plain": [
                            "<Figure size 640x480 with 1 Axes>"
                        ]
                    },
                    "metadata": {},
                    "output_type": "display_data"
                }
            ],
            "source": [
                "dx_lst = np.linspace(-.5,.5,100)\n",
                "\n",
                "import matplotlib.pyplot as pltq\n",
                "from py_wake.utils.plotting import setup_plot\n",
                "\n",
                "for i in range(3):\n",
                "    label=\"f([1,2,3])\".replace(str(i+1),f\"$x_{i}$\")\n",
                "    c = plt.plot(x[i] + dx_lst, [f(x + np.roll([dx,0,0],i)) for dx in dx_lst], label=label)[0].get_color()\n",
                "    plt.plot(x[i]+[-.5,.5], f(x) + df(x)[i]*np.array([-.5,.5]), '--', color=c)\n",
                "    plt.plot(x[i], f(x), '.', color=c)\n",
                "setup_plot(ylim=[0,40])\n",
                "plt.legend()"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "b9636f37",
            "metadata": {},
            "source": [
                "**In PyWake, gradients can be calculated via three methods: finite difference, complex step, and automatic diferentiation (AD) or autograd.**\n",
                "\n",
                "Below is the theoretical background of each method, followed by a comparison made between the three methods in terms of simulation time required."
            ]
        },
        {
            "cell_type": "markdown",
            "id": "80780155",
            "metadata": {},
            "source": [
                "### Finite difference `fd`\n",
                "\n",
                "$\\frac{d f(x)}{dx} = \\frac{f(x+h) - f(x)}{h}$\n",
                "\n",
                "Finite difference applied to the example function:\n"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 4,
            "id": "51ba6915",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "Analytical gradient: [6.129430520583658, 15.164788859062082, -45.83911438119122]\n",
                        "Finite difference gradient wrt. x0: 6.129437970514573\n",
                        "Finite difference gradient wrt. x1: 15.164782510623809\n",
                        "Finite difference gradient wrt. x2: -45.839169114714196\n"
                    ]
                }
            ],
            "source": [
                "print (\"Analytical gradient:\", list(df(x)))\n",
                "h = 1e-6\n",
                "for i in range(3):\n",
                "    print (f\"Finite difference gradient wrt. x{i}:\", (f(x+np.roll([h,0,0],i)) - f(x))/h)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "523117ef",
            "metadata": {},
            "source": [
                "In  this example the gradients are accurate to 4th or 5th decimal. The accuracy, however, is highly dependent on the step size, `h`. If the step size is too small the result becomes inaccurate due to nummerical issues. If the step size, on the other hand, becomes too big, then the result represents the gradient of a neighboring point.\n",
                "\n",
                "This compromize is illusated below:"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 5,
            "id": "7436be1b",
            "metadata": {},
            "outputs": [
                {
                    "data": {
                        "image/png": "iVBORw0KGgoAAAANSUhEUgAAAkIAAAG0CAYAAADehEiZAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAA9hAAAPYQGoP6dpAACrAElEQVR4nOzdd3gUVRfH8e9sSS8QQgu9Q6ghIBCQDgoIglhRQMVXEUWKKE0ggNJEQBBQQQVEpUgRlRaRJqFD6KEmBEIgpJBeNrvz/rEQQVrCbthscj7Pk8dkZvbsbzcxOczMvVdRVVVFCCGEEKIQ0tg6gBBCCCGErUgjJIQQQohCSxohIYQQQhRa0ggJIYQQotCSRkgIIYQQhZY0QkIIIYQotKQREkIIIUShJY2QEEIIIQotaYSEEEIIUWhJIySEEEKIQksaISGEEEIUWjpbB8hrly5donfv3kRHR6PT6RgzZgwvvPBCjh9vMpm4cuUK7u7uKIqSh0mFEEIIYS2qqpKUlISPjw8azf3P+ygFfdHVqKgorl27RoMGDYiOjqZhw4acPn0aV1fXHD3+8uXLlCtXLo9TCiGEECIvXLp0ibJly953f4E/I1S6dGlKly4NQIkSJfDy8iIuLi7HjZC7uztgfiM9PDyslstgMLB582Y6duyIXq+3Wt3HxZ7z23N2sO/89pwd7Du/PWcH+85vz9nBfvMnJiZSrly57L/j95PvG6EdO3bw+eefc/DgQaKiolizZg3du3e/45h58+bx+eefExUVRe3atZk1axZPPvnkXbUOHDiAyWTK1RmeW5fDPDw8rN4Iubi44OHhYVc/WLfYc357zg72nd+es4N957fn7GDf+e05O9h//ofd1pLvG6GUlBTq16/PG2+8Qc+ePe/av3z5cgYPHsy8efNo3rw533zzDZ06deLkyZOUL18++7jY2Fj69OnDwoULH/h8GRkZZGRkZH+dmJgImH8QDAaDlV4V2bWsWfNxsuf89pwd7Du/PWcH+85vz9nBvvPbc3aw3/w5zWtX9wgpinLXGaEmTZrQsGFD5s+fn72tVq1adO/encmTJwPm5qZDhw7873//o3fv3g98jsDAQMaPH3/X9p9//hkXFxfrvBAhhBBC5KnU1FR69epFQkLCA6/o5PszQg+SmZnJwYMHGTFixB3bO3bsSHBwMGC+a/z111+nbdu2D22CAEaOHMnQoUOzv751jbFjx45WvzQWFBREhw4d7PJUoz3nt+fsYN/57Tk72Hd+e84O9p3fnrOD/ea/dUXnYey6EYqJicFoNFKyZMk7tpcsWZKrV68CsGvXLpYvX069evVYu3YtAD/++CN169a9Z01HR0ccHR3v2q7X6/PkByCv6j4u9pzfnrODfee35+xg3/ntOTvYd357zg72lz+nWe26EbrlvzdCqaqava1FixaYTCZbxBJCCCFEPmfXM0t7e3uj1Wqzz/7cEh0dfddZIiGEEEKI/7LrRsjBwQF/f3+CgoLu2B4UFERAQICNUgkhhBDCXuT7S2PJycmcO3cu++uwsDBCQkLw8vKifPnyDB06lN69e9OoUSOaNWvGt99+S0REBP3797dhaiGEEELYg3zfCB04cIA2bdpkf31rRFffvn1ZtGgRL730ErGxsUyYMIGoqCjq1KnD+vXrqVChgq0iCyGEEMJO5PtGqHXr1jxsqqMBAwYwYMCAx5RICCGEEAWFXd8jJIQQQghhCWmEhBBCCFFo5ftLYwVVXHoc8aZ4rqRcQa+znwmqbjFkGew2vyHLQIaa8fADhRBCFHjSCNnIhL0T2JG4gy9++8LWUSxir/kdcaRUVClalm9p6yhCCCFsSBohG9Fr9OjQodVqbR3lkRmNRrvMb1SNZJgyGLVrFCu8VuDj5mPrSEIIIWxEGiEb+fzJz1m/fj2dO3e2q7VbbjEYDHabPzk9mZ6/9uRK5hWGbhvK4k6LcdTevb6cEEKIgk9ulhaFjqPWkVdcX8HTwZMTsSeYsm+KrSMJIYSwEWmERKFUVFOUzwI+Q0Hh1zO/svbcWltHEkIIYQPSCIlCK8AngHcbvAvAp3s+JTQu1MaJhBBCPG7SCIlC7Z167/BkmSfJMGYweOtgEjISbB1JCCHEYySNkCjUNIqGyU9OpoxbGSKTIxn1zyhMqsnWsYQQQjwm0giJQs/T0ZMZrWfgoHFgx+UdLDi6wNaRhBBCPCbSCAkB+Bbz5ZOmnwAwN2QuwZHBNk4khBDicZBGSIibelTrQc9qPVFRGb5zOFeSr9g6khBCiDwmjZAQtxnZZCS+xXy5kXGDD7d9SKYx09aRhBBC5CFphIS4jaPWkRmtZ+Dp6Mnx2OMy2aIQQhRw0ggJ8R9l3Mow5ckpKCisPLNSJlsUQogCTBohIe6hRZkWMtmiEEIUAtIICXEfMtmiEEIUfNIICXEfMtmiEEIUfDpbByislJNrqH51I5p/ToFGa+s4uaYxGal+9Yxd5teYjFSIuQqmpwD9A4+9Ndli7/W9sydbfKf+O48nqBBCiDwnjZCNaI7/Sq2oTRBl6ySPRgvUArvMrwUaAMaD1SFgwEOPvzXZ4tjgscwNmUtd77oElAnI65hCCCEeA2mEbESt3JbwuEzKlS+HVmN/VyiNJhOXIi7ZZX5TYhSas5vQ/PMF+PcGR/eHPqZHtR4cuX6EVWdXMXzncJY/sxwfN5/HkFYIIURekkbIRkyN+nEkujRlOndGq3/w5Zn8yGQwcGT9ervMb0xPJXWmH26pVyH4K2gzMkePG9lkJKfiTnEy9iQfbvuQxZ0W46B1yOO0Qggh8pJ9/VNeCGvQ6jlZ+nnz58FzIDk6Rw+TyRaFEKLgkUZIFEpRRRpj8mkIhhTYPi3Hj/vvZIu/nfstD1MKIYTIa9IIicJJUTC1HWv+/OAPEHs+xw9tUaYF79Y3T7Y4cc9EmWxRCCHsmDRCotBSK7SAqh3AlAVbP8vVY9+p/+9ki0O2DpHJFoUQwk5JIyQKt/bjAAWOr4Irh3P8sNsnW7ycfJnR/4yWyRaFEMIOSSMkCrdSdaHei+bP/wrM1UNvTbbooHFg++XtLDi6wPr5hBBC5ClphIRoMxq0DnBhG5z/O1cPvTXZIsDckLkERwbnQUAhhBB5RRohIYpWgMZvmT//KxBMubvE1aNaD3pW64mKyvCdw7mSfMX6GYUQQuQJaYSEAHhyGDi4Q9QROLE61w8f2WQkvsV8uZFxgw+3fUimMTMPQgohhLA2aYSEAHAtBs0HmT//eyJk5a6RkckWhRDCPskSGzaSYTCSYYTUzCz0qmLrOLlmMGTZbX6DIQujeo8dzQbAvm8hPhwOLoImb+eq7q3JFgf8NYCVZ1bSulxrWpZtaY3IQggh8og0QjbywfKj/H1ax8f7cndzbv5iv/nd9Vp86sTTtGqJfzc6uELr4fDnh7B9KjR4JUcLst6uRZkW9PHtw+KTixm/ezxrn12Lu0PuagghhHh85NKYKJSSDArv/XKEKzfS7tzRsC94VYbUGNg995Fqv+f3HuXdyxOdGs0XB76wQlohhCiY1p1fx9hdY206Ka2cEbKR2S/VY/3GTTz1VEf0drZ6O4DBYGDTps12mT85LYMeX24lMiWTd348yMr+zXDSa807tXpoNxZWvm5ekLXRm+BW4oH1/stZ58z4gPG8sekNVp1dxVMVn6KZTzPrvxAhhLBjsWmxTNs/jYSMBKoUqULf2n1tkkMaIRtx1Gtx1IKLgw693v6+DQZFtdv8ekWlXw0jc047cywygZGrjzHjxfooys17nXy7g09DuHIIdnwOnT/P9XM0KtWIl2u8zLLTywgMDmTNs2tw0btY94UIIYQdm7p/KgkZCdT0qkmvWr1slkMujYlCqZgTzH6pPlqNwprDkSzcGfbvTkWB9oHmzw98D3EXHuk5hvgPwcfVhyspV5h1aJbFmYUQoqDYcXkHG8I2oFE0BAYEotfY7sqCNEKi0Gpa2YsxXWoBMHnDKXacuf7vzsqtoEo784Ksf+duQdZbXPQuBAYEAvBL6C8cvHbQ0shCCGH3UgwpTNg9AYA+vn2oXay2TfNIIyQKtb4BFXmxUVlMKrz/8yHCY1L+3XnrrNDxX+FKyCPVb+bTjJ7VegIwdtdY0rLSHvIIIYQo2L489CXXUq9R1q0sAxoMsHUcaYRE4aYoChO718GvfBES07P435IDJGdkmXeWrgd1H21B1tt92OhDSriUICIpgrmHH20kmhBCFAQh0SEsC10GwNhmY3HWOds4kTRCQuCo0/L1a/6UcHfkbHQyQ5eHYDLdnHGx7WjQ6OHCVji/9ZHquzu4M7bpWAB+PPUjR64fsVZ0IYSwG5nGTMYFj0NF5dkqz+ab0bTSCAkBlPRw4pve/jhoNWw+eY0vt5w17yhaERr3M3/+CAuy3tKqXCueqfwMJtXE2F1jZS0yIUSh892x77iQcAEvJy8+avyRreNkk0ZIiJv8yhflsx51APhyy1k2Hr9q3tHyo5sLsobAyTWPXH/EEyMo5lSMCwkX+PrI11ZILIQQ9uH8jfN8e+xbwLxItaejp40T/UsaISFu80KjcrzRvCIAQ1eEcPpqErh6Q/MPzAdsyf2CrLd4OnrySdNPAPj++PecjD1pjchCCJGvGU1GxgWPI8uUReuyrXmqwlO2jnQHaYSE+I/RnWsRUKUYqZlG/rfkADdSM6HpAHAtAfFhcGjxI9duX6E9HSt0xKgaGbNrDAajwYrJhRAi/1l+ejlHrh/BVe/K6Kaj/528Np+QRkiI/9BpNXzVqyFlizoTEZfK+z8fJkvnAq0+Nh+wfSpkJD9y/ZFNRlLEsQhn4s/w3fHvrJRaCCHyn6jkKL489CUAgxsOppRrKRsnups0QkLcg5erAwv6NMJZr+WfczFM2RAK/q+bF2RNuf7IC7ICeDt7M+KJEQB8c/QbzsaftVJqIYTIP1RVZeKeiaRmpdKgeANerPGirSPdkzRCQtxHrdIefPFifQAW/hPG6iPXoK35Hh+CZ0Py9Qc8+sE6V+pM63KtyTJlMXbXWLJMWdaILIQQ+cbG8I3sjNyJXqMnMCAQjZI/W478mUqIfKJz3dIMbFsVgBGrj3HEow2UbgCZyeYFWR+RoiiMaToGd707x2OPs+TkEislFkII27uRfoMp+6YA8L96/6NKkSo2TnR/0ggJ8RBD2lenfa0SZGaZeGfpYeKbjzbvOPA9xIU9+MEPUMKlRPZcGnMPzyUs4dFrCSFEfvL5gc+JS4+japGqvFXnLVvHeSBphIR4CI1GYeZLDahS3JWriem8tdMNU+U2YDLA1kdbkPWW7lW7E+ATQKYpk7G7xmI0Ga2UWgghbCM4Mph159ehoJhXltfabmX5nJBGSIgccHfSs6BPI9yddBy8GM9X2tfMO46thKhHXzJDURQCmwXionMh5HoIy04vs1JiIYR4/FINqUzYY15ZvletXtQvXt/GiR5OGiEhcqhycTfmvOKHosCMY86Ele5k3mHBgqwApd1K82GjDwHzqsyXEi9ZmFQIIWxjbshcIpMjKe1amoF+A20dJ0ekERIiF1rXKMHHT9UE4M2LT2HS6OH833Bhm0V1n6/+PI1LNSYtK43A3YGY1Edb00wIIWzleMxxlp5aCsCYpmNw1bvaOFHOSCMkRC71b1WZrvV9CDOVYIXa3rwxaNwjL8gKoFE0jG82HietE/uu7uPXM79aKa0QQuQ9g8nAuOBxmFQTnSt15smyT9o6Uo5JIyRELimKwrSe9ajt48Hnad1IxfnmgqxrLapbzqMcHzQ0r2k24+AMopKjLA8rhBCPweITizkTf4YijkUY/sRwW8fJlULRCP3xxx/UqFGDatWqsXDhQlvHEQWAs4OWb/s0AtfifGPoDIC6ZQJYuHZYr5rmmwtTDCmM3zMeVVWtEVcIIfJMWEIY80PmA/Bx44/xcvKycaLcKfCNUFZWFkOHDuXvv//m0KFDTJ06lbi4OFvHEgVAmSLOzHu1IYvULlxXPVDiw+DgIotqajVaJjSfgIPGgV2Ru/jt/G/WCSuEEHnApJoYv3s8maZMAnwCeKbyM7aOlGsFvhHat28ftWvXpkyZMri7u9O5c2c2bdpk61iigGhSuRjDuvozO+s5ADL+nmLRgqwAlT0rM6DBAACm7Z9GdGq0xTmFECIvrDq7ioPXDuKsc2Zss7H5bmX5nMj3jdCOHTvo2rUrPj4+KIrC2rVr7zpm3rx5VKpUCScnJ/z9/dm5c2f2vitXrlCmTJnsr8uWLUtkZOTjiC4KideaVkD168NFUwkc02OI2zLT4pp9a/fFt5gvSZlJTNwzUS6RCSHynejUaGYcmAHAQL+BlHEr85BH5E/5vhFKSUmhfv36fPXVV/fcv3z5cgYPHszo0aM5fPgwTz75JJ06dSIiIgLgnn9A7LFjFfmXoiiM7e7HqqJvAOC07yuS4yy70Vmn0TGx+UR0Gh3bLm1jY/hGKyQVQgjrmbR3EsmGZOoUq0Ovmr1sHeeR6Wwd4GE6depEp06d7rt/xowZ9OvXj7feMq9lMmvWLDZt2sT8+fOZPHkyZcqUueMM0OXLl2nSpMl962VkZJCRkZH9dWJiIgAGgwGDwbIbYW93q5Y1az5O9pw/L7IrwMt93if0q5XUVC/w1/cf0fTdBTg6PPr/YpXcKtGvdj++OfYNk/ZOwt/bn6JOReW9tyF7zm/P2cG+89tzdrh3/i2XtrAlYgs6RccnT3yCyWjCZMxf85/l9P1WVDs6564oCmvWrKF79+4AZGZm4uLiwsqVK+nRo0f2cYMGDSIkJITt27eTlZVFrVq12LZtGx4eHjRs2JA9e/ZQrFixez5HYGAg48ePv2v7zz//jIuLS568LlFwqNHH6R45DYBTShWiy3XlhlcDUB7t5GuWmsXXSV9z1XSVOvo6vOz6shXTCiFE7qWZ0vgy6UuS1WRaObaig3MHW0e6p9TUVHr16kVCQgIeHh73PS7fnxF6kJiYGIxGIyVLlrxje8mSJbl69SoAOp2OL774gjZt2mAymfj444/v2wQBjBw5kqFDh2Z/nZiYSLly5ejYseMD38jcMhgMBAUF0aFDB/T6/L0g3b3Yc/68zd6Z8N/SKHXsa2pxnloRs8hIrom25RDUWt1Bo811xapxVem7qS/HDcdxrOtIy1It5b23EXvOb8/Zwb7z23N2uDv/xL0TSU5MpoJ7BaZ0noKj1tHWEe/p1hWdh7HrRuiW/97zo6rqHdu6detGt27dclTL0dERR8e7v6l6vT5PfoDzqu7jYs/58yp7xec/5WzDN9j900R6ZG3EPS4U1r4DO6ZCiyFQ72XQOeS4Xv2S9XmjzhssPLaQKfun0KhLozzN/zjYc3aw7/z2nB3sO789Zwdz/sMxh1lzfg0AgQGBuDm5WVQzLSEWVQEXj/ufoHhUOX2v8/3N0g/i7e2NVqvNPvtzS3R09F1niYR4nKpVrkLHD77mzSI/8IXheW6obhB3AdYNhNl+sPcbMKTluF7/+v2p5FmJ2PRYvjj0RR4mF0KIe0vPSmf8bvOtIy9Wf5FGpRpZXPPUj4NJn+FH6PYVFtd6VHbdCDk4OODv709QUNAd24OCgggICLBRKiHMSnk68cOADhyp8g4BGbP5LOtVUh28IfEybPgYZtWFnTMg/eGnbx21jkwImICCwh9hf3DacPoxvAIhhPjXguMLiEiKoIRzCQb7D7a43pmDf9MwZh1eJJCmtezMkiXyfSOUnJxMSEgIISEhAISFhRESEpI9PH7o0KEsXLiQ77//nlOnTjFkyBAiIiLo37+/DVMLYebmqOO7vo3o2qgaC7K64Jc4nY0VP0YtUh5SrsOW8TCrDvz9GaQ+eMbzBiUa0Nu3NwB/pP1BpjHzcbwEIYQgKiuKJaeWADC66WjcHdwtqmcwGFDWDwNgn8dT+LXobHHGR5XvG6EDBw7g5+eHn58fYG58/Pz8GDt2LAAvvfQSs2bNYsKECTRo0IAdO3awfv16KlSoYMvYQmTTazVM6VmXDztUJwMH+oc2YFDx78jsOg+8q0N6AuyYBjPrwKbRkHj/OYjea/Ae3k7exJviWXVu1WN8FUKIwirLlMWatDUYVSMdKnSgbfm2FtfctWI61YznScKFqq/a9nJ/vm+EWrdujaqqd30sWrQo+5gBAwYQHh5ORkYGBw8epGXLlrYLLMQ9KIrCwHbVmPFifXQahXXHrvPq/krceGMnvLgEStUDQwrs/gq+rAd/DIH4i3fVcdG78HbdtwHzaerkTMuW8xBCiIf55fQvXDFewV3vzqgmoyyuFx5xEb8zcwC4UHcwXiXLWVzTEvm+ERKiIHmuYVkWv/kE7o469ofH89zXe7hUqgO8swNe/RXKNQVjJhz43nxT9Zr+cP3MHTWerfIs3hpvbmTc4IcTP9jolQghCoNLSZeYf9S8svyQhkPwdva2qJ7JpHLhl2F4Kilc1FehXvehD39QHpNGSIjHrHlVb359NwAfTycuXE+hx7xdHLmcANU6QL9N8Pp6qNIWVCMc+QXmPgHLe0PUEQD0Gj0dnMwTmP148keup1635csRQhRQqqoyPng86cZ0Kukq8WzlZy2u+VfQ77RN2wyAU/dZKFrbTycgjZAQNlCjlDtr3muOb2kPYpIzefnbPQSdvGbeWbE59F4D//sbaj4DqHBqHXzTEpY+j3JpL756X+oUq0NaVhpfH/napq9FCFEwrT23lr1X9+KodaS7c3eL1+mMvpFCud1jADhd+llK1s4ft7FIIySEjZT0cGJF/2a0rF6cNIORd348wI+7w/89oIw/vPwTvLsb6r5oXqbjXBC6JV2oE/kLg/wGAbDq7CrCEsJs8yKEEAXS9dTrfH7gcwD61+1PMa3lEx7+vXQKtQgnWXGlaq/8Mx+aNEJC2NCt4fUvNy6HSYUxv51g8vpTmEy3LQFY0hd6LoCBB6FhXwCqXN+Ev+pIq7KtMKpG5hyeY6NXIIQoiCbtnURSZhK+xXx5tearFtf7+8AJOl9fCEBS81Fo3YtbXNNapBESwsb0Wg2Tn6vLsI7VAfhmxwUGLjtMusF454FelaHbbEy+3VFQ0f49kUENB6GgEHQxiCPXj9ggvRCioPnr4l/8FfEXOkXHhIAJ6DSWrcaVkGYg5c/ReCipXHWtQem271opqXVIIyREPqAoCu+3NQ+v12sV/jwaRe/v9nIj9e5JE42tR2NStGgubKFafCTdqpjX0Zt5cCaqqt51vBBC5FRCRgKf7f0MgDfqvEENrxoW1/xl1Qq6qlsBKPrCnEdafDovSSMkRD7yXMOyLH7jCdydbg6vnx9MRGzqnQcVrUS4980JzYLG8n79AThoHDh47SA7I3c+/tBCiALjiwNfEJMWQ0WPirxT/x2L6+09d41WZ6YAcK3qSzhWbGJxTWuTRkiIfCagqje/9v93eP1z83dx5NKNO445XfJZVAc3iDpCqfBgXq1lvoY/8+BMjCbjPaoKIcSD7Ynaw5pz5pXlxweMx1HraFG9dIORfSumUUsTQarWnZI9JlsjptVJIyREPvTf4fUvfbv73+H1QKbeA1OzD8xfbJlAv1qv4e7gzrkb5/j9wu82Si2EsFephlTGB5tXln+pxks0LNnQ4po/bNpD34yfAFDajwNXy0ee5QVphITIp24Nr29VvTjpBhPv/HiAJbcNrzc98Q64lYIbF/E8tor/1f0fAF8d/or0rHQbpRZC2KO5IXO5nHyZUq6lGNxwsMX1Qq8mUmrvZDyUNG4UrYNzkzctD5lHpBESIh9zc9Sx8Lbh9WN/O8GUjacxqYCDK7QZaT5w+zReqdiFki4luZZ6jWWhy2yaWwhhP47HHGfpqaUAjGk6BjcHN4vqGU0qi3/5mR7anZhQ8Ow5O9/dIH07aYSEyOf+O7z+u10XWR1+83/dBq+ZV7BPi8Npz3zea/AeAAuOLSAhI8FWkYUQdsJgNDA2eCwm1UTnSp1pWdby2Z6X/HOWvvFfAZBe9zWUsv4W18xL0ggJYQduH14P8M9VhRNXEkGrg/aB5oP2zKdbiUZULVKVxMxEvjv+ne0CCyHswnfHv+Ns/FmKOhZl+BPDLa53OT6Vq3/NoabmEhl6T1w6TbBCyrwljZAQduS5hmXpWq8UKgqTN542zxtUozOUbwZZaWi3Tc2+vv/TyZ+4mnLVpnmFEPnXhRsX+PbotwAMf2I4Xk5eFtVTVZXPf93O+8pKAPRPTQAXy2o+DtIICWFnhnWohl5R2RsWz1+nokFRoMPNf3WF/ERLhxI0LNGQTFMmc0Pm2jasECJfMpqMjA0ei8FkoGXZlnSu1NnimuuOXKF1xBzclTTSS/ihadjHCknznjRCQtgZnyLOtPIxzyA9af0pMrNMUO4JqNUVVBPKlvEMbTQUgHXn13E2/qwt4woh8qFlp5dx5PoRXPWujGk6xuKV5eNSMvl93Up6aHehouDUfSZo7KPFsI+UQog7dPAxUczVgbCYFH7ae9G8sd04ULRwZgP1U5JpX749JtXE7EOzbRtWCJGvXEm+wpeHvgRgcMPBlHItZXHNSb8f5aOsBQCY/N8AHz+Laz4u0ggJYYecdDC4XVUAZv111rwmmXc18DevTk/QWD7wG4hW0bLt8jYOXjtow7RCiPxCVVUm7J5AWlYaDUs05MUaL1pcc/uZ63ge+54amssYnLzQthtjhaSPjzRCQtip5xv6UKOkOwlpBub8fc68sdUI0LtC5AEqRR7luWrPATDj4AxZkFUIwR8X/mDXlV04aBwIDAhEo1jWBqRmZjFj9XaG6FYBoO9oHzdI304aISHslE6rYXSXWgAs2R1OeEwKuJeEgIHmA7ZM4N06b+Gsc+bo9aP8HfG3DdMKIWwtNi2WqfunAtC/fn8qeVayuOaMzWfol7IQNyUdo08jaPCqxTUfN2mEhLBjLasXp3WN4hiMKlM2hJo3BrwPrsUh7jzFT/3Ja7VeA2DWoVlkmbJsmFYIYUtT9k0hISOBGkVr8Hqd1y2ud+TSDU4F/0E37W5URYP2mS/s5gbp29lfYiHEHUZ1roVGgY0nrrL3Qiw4ukOrmxOjbZvCm9VfpIhjEcITw7NXlhZCFC7bLm1jY/hGNIqG8c3Ho9foLapnMJoY/etBAnWLAFAa9QOfBhbntAVphISwc9VLuvPKE+UB+PTPU5hMKvi/Dl5VIDUGt/3f8069dwCYFzKPVEOqDdMKIR63pMwkJu6ZCEDf2n2pXay2xTW/3XGBgJiVVNNEYnL2hrajLa5pK9IICVEADOlQHTdHHcciE1gbEglaPbQba94Z/BUv+rSijFsZYtJishdXFEIUDjMPziQ6NZry7uUZUH+AxfXCYlJYtmUPg3SrAdB0nADORS2uayvSCAlRAHi7OfJeG/Nw+mkbT5OWaQTfZ6FMIzCk4PDPDAb6mW+i/v7498Snx9syrhDiMdl/dT8rz5iXvAgMCMRJ52RRPZNJZcSqowxXfsRVyUAt1wTqv2KNqDYjjZAQBcQbzStSpogzVxPTWbDzgnnpjY7m0+EcXEwn96rU8qpFiiEle30hIUTBlZ6Vzvjd4wF4vvrzNC7V2OKaKw5cQndxO89o96AqGpTO0+3yBunb2Xd6IUQ2J72WEZ1qAvD19vNEJ6ZDhQCo3glUI5otExjsPxgwT69/OemyDdMKIfLa/CPzuZh4kRLOJRjqP9TietFJGUxdf4wJt26Qbvw/KF3P4rq2Jo2QEAXIM/VK41e+CKmZRr7YfMa8sX0gKBoI/YOALC1NSzcly5TFVyFf2TSrECLvnIw9yeITiwEY3XQ07g7uFtec8McpXjKso4omCtW1OLQZZXHN/EAaISEKEEVR+KSLLwArDl7i5JVEKFHz30nOgsYyuOFgAP688CenYk/ZKKkQIq8YTAbGBY/DqBp5quJTtC3f1uKaR+MUjp48xQc68xQcSoeJ4FzE4rr5gTRCQhQw/hWK8ky90qgqfPrnSfPSGm1Ggc4ZLu2hdkw4nSp1AsyTLAohCpbFJxYTGheKh4MHI54YYXG9pHQDv17Q8In+R1yUDCjfDOq/bIWk+YM0QkIUQMOfromDTkPw+Vj+Do0GDx9odnPY7F+BDKw3AJ1GR/CVYHZf2W3bsEIIqwlPCGd+yHwAPm78Md7O3hbX/HzzWeoZj9FFuw9V0ULn6ebBGAWENEJCFEDlvFx4s7l5HaFJ609hMJqg+SBw9oKYM5Q7v40Xq5tXnZ55cCYm1WTLuEIIKzCpJgJ3B5JpyiTAJ4BuVbpZXHNfWByr9ocRqDPfb6Q0eQdK1bG4bn4ijZAQBdSANlUo5urA+esp/LIvApw8odXH5p1bJ/FOrd646l05FXeKTeGbbBtWCGGxX8/8ysFrB3HWOTO22VgUC8/apBuMjFh1lLe062/eIF0CWlt+qS2/kUZIiALKw0nPkA7VAZgZdIaENAM0ehOKVIDka3gd/oXXa78OwOxDszEYDTZMK4SwxNWUq8w4OAOAQQ0HUcatjMU1Z285S0ZMOB/ozTdIG9uPN/+DqoCRRkiIAuzlxuWoVsKN+FQDc7eeA53jv0tv7PqSPhW7UMypGJeTL7PizArbhhVCPBJVVfl0z6ekGFKoV7weL9ew/EbmE1cS+GbHecbrF+FEJjFuNVBrP2+FtPmPNEJCFGA6rYZRXWoBsGhXOBdjU6D2c1C6AWQm4bJrDgMamG+i/ubINyRnJtswrRDiUWwM38j2y9vRaXSMbzYerUZrUb0so4nhq47Sid201x5G1eg5Wvb1AnWD9O2kERKigGtdvThPVvMm02hi6sZQ83T4HSaYdx74jh5e9angUYH4jHgWn1xs27BCiFy5kX6DKfumAPB2vbepWrSqxTW/+yeMy5GRTHAw/z4wNR9CkrPll9ryK2mEhCjgFEVhdJdaaBRYf+wqB8LjoHIrqNoeTFnot03mA78PAPP8IzFpMTZOLITIqWn7pxGXHkfVIlV5q85bFtcLi0lhRtAZRut+wotEKF4TU8AgKyTNv6QREqIQqFnKg5calwdg4p+nMJlUaD8eUODEGjrovKjrXZe0rDS+PvK1bcMKIXLkn8h/+P3C72gUDRMCJqDX6i2qp6oqI1cfpbHpCC/odqCiQLc55nsLCzBphIQoJIZ2qI6rg5Yjl27w+9Er5rlAbs4Oq/wVyJCGQwDzENzwhHAbJhVCPEyKIYUJu82XuF+t9Sp1i9e1uOay/Zc4cuEKk/XfAaA88TaUe8LiuvmdNEJCFBLF3R0Z0MZ8/8DUDaGkG4zQZjRoHSF8J42T4nmyzJMYVSMLjy20cVohxIN8eehLolKiKONWhvcbvG9xvasJ6Uz68xRDdKsop0SDR1loN8YKSfM/aYSEKET6taiEj6cTVxLS+e6fMChSDpq8Y9751zjermu+x2B92Hq5V0iIfOpw9GGWhS4DYFyzcbjoXSyqp6oqY347TsXMM/TTbTBvfGYmOFq+Yr09yHUj9Oabb5KUlHTX9pSUFN58802rhBJC5A0nvZbhnWoCMG/rOaKT0uHJoeBUBKJP0uDKSeoVr4fBZMj+RSuEyD8yjBmMCx6Hikr3qt1p5tPM4prrj11l68lIpuoXoMUEdV+A6h2tkNY+5LoRWrx4MWlpaXdtT0tLY8mSJVYJJYTIO13r+VC/XBFSMo3MDDoLzkXhyQ/NO7dOonf1lwBYcXoF6VnpNkwqhPivb49+S1hCGN7O3gxrNMzievEpmYxbd5y3tX/iq7loXo/w6SlWSGo/ctwIJSYmkpCQgKqqJCUlkZiYmP0RHx/P+vXrKVGiRF5mFUJYgUajMObmJIvL90cQejURnngbPMtBYiTto85S2rU08Rnx/HnhTxunFULccjruNN8f+x6AUU1G4elo+XIXn/55CveUiwzWrzZveHoyuFq+Yr09yXEjVKRIEby8vFAUherVq1O0aNHsD29vb958803ee++9vMwqhLCSRhW96FK3NCYVPvvzFKrO0XzjNKD750terdIDgB9P/oiqqraMKoQAskxZjAseR5aaRfvy7elQoYPFNXecuc7qQxFM1i/EAQNUaQv1XrJCWvuiy+mBW7duRVVV2rZty6pVq/Dy8sre5+DgQIUKFfDx8cmTkEII6xv+dE2CTl5j59kYtp25Tpt6L8Lur+DacZ67GsY8nQvnE84TfCWY5mWa2zquEIXa0pNLORF7AncHd0Y1GWVxvZSMLEauPsZL2m001ZwCvQs8M6vALqPxIDluhFq1agVAWFgY5cqVQ6ORAWdC2LPyxVx4vXlFvt1xgc/+PMWTg55E1z4Qfnoe9wOLeK71Oyy9sJYlJ5dIIySEDUUkRjA3ZC4AHzX6iOIuxS2uOX3zaQw3rjDa6WfzhrZjoGgFi+vaoxw3QrdUqFCBGzdusG/fPqKjozGZTHfs79Onj9XCCSHy1nttqrLywCXORSezbP8lXmvSHio0h4u76BUTxU8oBF8J5lz8OausYSSEyB1VVRm/ezzpxnSalG5C96rdLa55KCKeRcHhzNcvwp1U8Gn47zQahVCuG6Hff/+dV199lZSUFNzd3VFuO42mKIo0QkLYEU9nPUM6VGfsbyeYGXSGbg188Gg3Dr7vSLmjq2nXtCd/Xd3D0lNLCQwItHVcIQqd1WdXs+/qPpy0ToxrNu6Ov7mPIiPLyPBfj9JR2cfT2v2g0ZmX0bBwxXp7luvrWx9++GH2XEI3btwgPj4++yMuLi4vMgoh8tArT5SnSnFXYlMymbf1PJRvAtWfBtVI7/h4AH4//zuxabE2TipE4RKdGs0XB74A4H2/9ynnXs7imvO2nuda9DU+c1hk3tB8sHm5nUIs141QZGQkH3zwAS4uls1kKYTIH/RaDaNvDqf//p8wLsWlmu8XQMEvNIg6HpXJNGWy4swK2wYVohBRVZVP93xKkiGJut51ea3WaxbXPHMtiXnbzjFC9zPe3IBi1aDlR5aHtXO5boSeeuopDhw4kBdZhBA20qZGCZpXLUam0cTUjaHmfyHWfQEF6J2UCsCy0GVkGDNsG1SIQmLzxc1svbQVnaIjMCAQrYWXrowmlY9/PYq/eoJeuq3mjd1mg97JCmntW67vEerSpQsfffQRJ0+epG7duuj1+jv2d+vWzWrhhBCPh6IojO7sS5c5O/njaBSvB8TRqM1IOLGaDhf2MaNmfa6lx7H+wnp6VOth67hCFGgJGQlM2jsJgH51+1G9aHWLay4KDufUpWg2OZpXlqfRm1AhwOK6BUGuG6H//e9/AEyYMOGufYqiYDQaLU8lhHjsfH08eNG/HMsPXGLIihD+GPgkng37oj/wHb1SDczUwo+nfqR71e4W37AphLi/afunEZceR2XPyrxd722L612KS2X6ptMM0q2mohIF7qWhfaDlQQuIXF8aM5lM9/2QJkgI+zaqSy3KFnXmUlwaI1YdRW35Eeic6Xn5FM4aPWfjz7Inao+tYwpRYAVHBrPu/DoUFMYHjMdB62BRPVVVGbXmGJWyzvOO7g/zxi5fgJPly3MUFBbNipieLgsyClGQeDrr+apXQ/RahQ3Hr/LjiQxo2h9Pk0r3m7cH/XjyR9uGFKKASjWkMn73eAB61epFgxINLK7568HLBJ+9xlSHheaV5X27Q80uFtctSHLdCBmNRiZOnEiZMmVwc3PjwoULAIwZM4bvvvvO6gGFEI9Xg3JFGP50TQA+/eMUJyu/AU6evHb1IgqwM3InF25csG1IIQqgOYfncCXlCj6uPnzg94HF9a4nZfDpn6d4Q7uRusoF81mgTtOskLRgyXUj9Nlnn7Fo0SKmTZuGg8O/p+zq1q3LwoULrRrOGi5dukTr1q3x9fWlXr16rFy50taRhMj3+rWoRPtaJck0mnh31QUymgykfFYWrTPN+5eeWmrbgEIUMCHRIfx06icAxjYbi4ve8ilqAtedwCP9MsP0v5o3dPwM3EtaXLegyXUjtGTJEr799lteffVVtNp/h/PVq1eP0NBQq4azBp1Ox6xZszh58iR//fUXQ4YMISUlxdaxhMjXFEVh+gv1KFPEmYuxqYyMDEB1K0nv2GuAeYLF+PR4G6cUomDINGYSGByIikq3Kt2ssrbfphNX+fPYFSbrv8OJDKjUEvwsn4uoIHqkCRWrVr17zSGTyYTBYLBKKGsqXbo0DRo0AKBEiRJ4eXnJDNhC5EARFwdmv+KHTqOw+vgN9pfvR6P0DGoZTKQb01l5Rs6uCmENC48t5HzCebycvPiokeUTHCakGRiz9jjPa3fQQnMcdE6FdmX5nMh1I1S7dm127tx51/aVK1fi5+eX6wA7duyga9eu+Pj4oCgKa9euveuYefPmUalSJZycnPD397/n8+fEgQMHMJlMlCtn+TTlQhQG/hWK8tFTNQB446gvBvfy9I43/0Pil9BfyDRm2jKeEHbvbPxZFhxbAMDIJiMp4lTE4ppTNpzClBTNWL35UhttRkGxKhbXLahyPY/QuHHj6N27N5GRkZhMJlavXs3p06dZsmQJf/zxR64DpKSkUL9+fd544w169ux51/7ly5czePBg5s2bR/Pmzfnmm2/o1KkTJ0+epHz58gD4+/uTkXH3jLebN2/Gx8cHgNjYWPr06ZMv72MSIj/735OV2RsWx9+h0Xye2ZOPM2Yy02jieloMG8M30q2KTKIqxKMwmoyMCx5HlimLNuXa8FSFpyyuGXw+hl/2XWKOfjEeJEOpetD0PSukLbhy3Qh17dqV5cuXM2nSJBRFYezYsTRs2JDff/+dDh065DpAp06d6NSp0333z5gxg379+vHWW28BMGvWLDZt2sT8+fOZPHkyAAcPHnzgc2RkZNCjRw9GjhxJQMCDZ9LMyMi4o6lKTEwEwGAwWPXS361a+fFyYk7Yc357zg62yT+lhy/d5iawMMGf1z0q0yshhi+9irDkxBKeLvd0jidYlPfeduw5O9h3/vtlXxq6lGMxx3DTuzHcfzhZWVkWPU9appERq47STnOQrto9qIqWrM4zwaSC6dHfN3t973OaV1FVVc3jLDmmKApr1qyhe/fuAGRmZuLi4sLKlSvp0ePfaf0HDRpESEgI27dvf2hNVVXp1asXNWrUIDAw8KHHBwYGMn78+Lu2//zzz7LQrCjULiTCnBNa2mgOMcNpJu3LlSFdo/Cm65tU1le2dTwh7EqcMY45SXMwYOBZ52dp7NjY4pq/XdSw70o6fzl+TCkljrMlunCyzEtWSGufUlNT6dWrFwkJCXh4eNz3uFyfEXqcYmJiMBqNlCx553C/kiVLcvXq1RzV2LVrF8uXL6devXrZ9x/9+OOP1K1b957Hjxw5kqFDh2Z/nZiYSLly5ejYseMD38jcMhgMBAUF0aFDh7vWa7MH9pzfnrODbfPrd4QxPQguGKvwbHIMyz3cOVfkHO+3ej9Hj5f33nbsOTvYd/7/ZldVlQFbB2BIMtCoRCPGthtr8bI1xyIT2LZnL4G65ZRS4lCLVqLi619TUe9s9fz24tYVnYfJUSPk5eXFmTNn8Pb2pmjRog/8huXFiKz/Pp+qqjn+oWnRogUmkynHz+Xo6Iijo+Nd2/V6fZ78AORV3cfFnvPbc3awTf4Bbaqx/+INJp99mamJk1nu4c7OyJ1EpkZS0bNijuvIe2879pwd7Dv/rexrzq5h79W9OGodGd98/B1z8j0Kg9HEqLUn8eM0fXRBACjdZqN3sd4/3sH+3vucZs1RIzRz5kzc3d0B8z06j4u3tzdarfausz/R0dF3nSUSQuQ9jUZhxov16Tw7kYtptWmZeoUdLs4sPbWUT5p+Yut4QuR711Ov8/mBzwF4r8F7lPcob3HNb3dc4MLVODY63RwM5NfbPG+QyJEcNUJ9+/a95+d5zcHBAX9/f4KCgu64RygoKIhnn332seUQQvyrmJsjs1/2Y+LClxiTMJ4dLs6sO7eWgX4D8XSUhRyFeJDJ+yaTlJmEbzFfevv2trje+evJfLnlLO/pfqMykeBaAjpOtELSwiNHjVBOr7MBub6PJjk5mXPnzmV/HRYWRkhICF5eXpQvX56hQ4fSu3dvGjVqRLNmzfj222+JiIigf//+uXoeIYT1NKlcjKfadSR6229Uz7jIGUf49cyv9Kvbz9bRhMi3tlzaQtDFIHSKjgkBE9BpLLtN12RSGbHqKBWNF3nPcZ15Y+fPwbmoFdIWHjn6LhQpUiTH9+QYjcZcBThw4ABt2rTJ/vrWjcp9+/Zl0aJFvPTSS8TGxjJhwgSioqKoU6cO69evp0KFCrl6HiGEdQ1oU5XhZ97h1YQPGFfCi5+PL6JP7T7oNfZzD4EQj0uaKY1Z+2cB8EadN6jhVcPimj/tvcjB8FjWOC5ARxbUfAZ85WpJbuWoEdq6dWv25+Hh4YwYMYLXX3+dZs2aAbB7924WL16cPa9PbrRu3ZqHjeAfMGAAAwYMyHVtIUTe0WoUhr/2DNtmLKVY1mmiucHmsE10qfKMraMJke9sSN9ATGYMFT0q8k79dyyuF3kjjSkbQumr3UR95Rw4epjPBskyGrmWo0aoVatW2Z9PmDCBGTNm8Morr2Rv69atG3Xr1uXbb799rPcQCSFsq7i7I5W6T+CFv7vytZc78/Z8SefKXSweCixEQbL36l4OZR4CYHzAeBy1d49Mzg1VVflkzTGKGq4y3HGFeWOH8eDhY2nUQinXa43t3r2bRo0a3bW9UaNG7Nu3zyqhhBD2o1H9utRybY+jyURE1lV+D320tQCFKIhSDal8uvdTAF6s9iINSza0uOa6I1fYejr635XlK7SAhq9bXLewynUjVK5cOb7++uu7tn/zzTeymKkQhVSrXlN5OsW8AOv8HZNJN+TuXkEhCqq5IXOJTInEU/FkYIOBFteLTc4gcN0Jemp28qTmqHll+W6zQZPrP+fiplzfsj5z5kx69uzJpk2baNq0KQB79uzh/PnzrFq1yuoBhRD5n9atGC9Veo7fYtYT6XiJEWuDmPXC07aOJYRNHbt+jKWnlgLQzaUbrnpXi2tO+OMk2tQYAp2Xggq0HiEry1so1y1k586dOXv2LN26dSMuLo7Y2FieffZZzpw5Q+fOnfMioxDCDtRt/wkB6VmoisL5yNmsO3LF1pGEsBmD0cDY4LGYVBOdKnaiht7yUWJ/h17jt5ArBOoX464mQ+n60Mzys0yF3SNNYlC2bFkmTZpk7SxCCHvm6E7fqs8RfHkdVz0jGLdmJ3XLPEMlb8v/FSyEvVl4fCHnbpyjqGNRhjUcxu6/d1tULyndwOg1x+mgOcAz2j2gaKHbV6DN10uG2oVHvqiYmppKaGgoR48eveNDCFF4NWs5hqpZKukahTpuS3nvp0Nyv5AodM7fOM+3R78FYMQTIyjqZPkEh1M3hpKSEMskx0XmDc0/gNL1LK4rHqERun79Os888wzu7u7Url0bPz+/Oz6EEIWXoneid0XzJfIrRc9zKeoKn/15ysaphHh8jCYjY4PHkmXKolXZVnSq1MnimvvC4li6J4IRup8prsZBsarQargV0gp4hEZo8ODBxMfHs2fPHpydndm4cSOLFy+mWrVqrFu3Li8yCiHsSJeWgXiZIFqnpW2Rpfy45yLrj0XZOpYQj8Wy08s4ev0ornpXPmn6icVzaqUbjIxYdZSmmpP00t2c3LjrbNA7WyGtgEdohP7++29mzpxJ48aN0Wg0VKhQgddee41p06Y90szSQoiCxVHvwktl2wJwzessxbjB8F+PcjE2xcbJhMhbkcmRfHnoSwCG+g+llGspi2vO3nKWKzFxTHO4ubJ8ozehYnOL64p/5boRSklJoUSJEgB4eXlx/fp1AOrWrcuhQ4esm04IYZdebD4GBxVOOOrpV2IVSRlZvP/zYTKyTLaOJkSeUFWVCbsnkJaVhn9Jf56v/rzFNY9HJvDNjgsM1q2iPFfBowy0H2+FtOJ2uW6EatSowenTpwFo0KAB33zzDZGRkXz99deULl3a6gGFEPbH28WbLqXM84ydczqKr3M8xyITmLbpjI2TCZE31p1fR/CVYBw0DgQ2C0SjWDbBYZbRxPBVR6mlnudt3Xrzxi4zwMnDCmnF7R7pHqGoKPP1/nHjxrFx40bKly/P7NmzZUi9ECJb7yYfA7DFxYnPKvwJwJI9ERyJlXXIRMESkxbDtP3TAHi3wbtU9Kxocc0FO8M4fSWO6Y4L0GCCOj2hhkxSmhdyPQHBq6++mv25n58f4eHhhIaGUr58eby9va0aTghhv6oVrUYzr9rsjjtBUMJuRjV6jUkH4JfzGnrFplK1lKetIwphFZP3TiYxM5FaXrXoW9vyhccvXE9m1l9neFv7BzW5CM5e8PRUKyQV95KrM0IGg4HKlStz8uTJ7G0uLi40bNhQmiAhxF16+70HwGp3V17OXIJfOU/SjArv/HSYxHSDjdMJYbktEVvYfHEzWkXL+IDx6DV6i+qZTCojVh+jjPEyg/VrzBufngJuxa2QVtxLrhohvV5PRkaGxcMBhRCFQ/MyzansVpYUjYa1V3fxTRsTng4q56+nMOiXwxhNqq0jCvHIEjMT+WzPZwC8Xvt1ahWrZXHNX/ZHsD8shmkOC3HAAFU7QL0XLa4r7i/X9wgNHDiQqVOnkpWVlRd5hBAFiEbR8FrdNwH42cOdovum8r8aRpz0Graevs7UjaE2TijEo5txYAbX065TwaMC/ev3t7heVEIaU9aH8qp2C42UUHBwg2dmgJx8yFO5vkdo7969bNmyhc2bN1O3bl1cXe9cR2j16tVWCyeEsH9dK3dl9sFZRJLItmsHaVj6OFN69GHwiqN8u+MC1Uu687x/WVvHFCJX9kXtY9XZVQAENgvESedkUT1VVRmz9jhuGdcY7bzMvLJ8u3FQpLwV0ooHyfUZoSJFitCzZ0+eeuopfHx88PT0vONDCCFu56Rz4sWaLwOwxNODWlEr6VKnJB+0rQrAqNXHOHgxzpYRhciVtKw0AncHAvBi9RdpVKqRxTX/OBrFX6euMcnhe5zVNCjXBBq/ZXFd8XC5PiP0ww8/5EUOIUQB9nKNl/n+2PeEOMGluEhq/zOdwe1HcuZaMhtPXOWdHw/y2/stKFNElg0Q+d+8kHlcSrpESZeSDPEfYnG9+JRMAtedoJsmmDaaw6B1gG5zQGPZXEQiZ+RdFkLkueIuxelc2bwY648e7mh3TEVzbAUzXqpPrdIexCRn8r/FB0jNlHsPRf52IuYES04uAWBM0zG4ObhZXHPiHydRU2KY4PijeUPLj6F4DYvripzJ9RkhPz+/e44aUxQFJycnqlatyuuvv06bNm2sElAIUTD08e3DuvPr2Ozqyrs3Eqj823u4ePiwoI8/3efu4mRUIh+uOMLcXg3RaOTmUJH/GEwGxgaPxaSa6FSpE63KtbK45rbT0aw+HMks/RKKqIlQsg40H2SFtCKncn1G6Omnn+bChQu4urrSpk0bWrdujZubG+fPn6dx48ZERUXRvn17fvvtt7zIK4SwUzW8atDCpwUmBYaWq0yqmgXLX6Vs1iW+fs0fvVZhw/GrzNpy1tZRhbinH47/wJn4MxRxLMKIJ0ZYXC85I4vRa47TRnOY7tpgUDTmS2I6ByukFTmV60YoJiaGDz/8kJ07d/LFF18wY8YMduzYwbBhw0hJSWHz5s188sknTJw4MS/yCiHs2NgmY3FT3DivpjO+fDXU9AT46XkaeWcxqUddwLza9h9Hr9g4qRB3unDjAl8f+RqA4U8Mx8vJy+Kan28MJeFGLFMcb95723QAlGlocV2RO7luhFasWMErr7xy1/aXX36ZFStWAPDKK69kL8wqhBC3eDt787Lry2gVLes16SwvVRFuRMDPL/FCvWK81aISAMNWHuF4ZIJtwwpxk0k1MS54HAaTgRZlWtClUheLax4Ij2PJnot8rFtOSTUGilaENqMtDytyLdeNkJOTE8HBwXdtDw4OxsnJPI+CyWTC0dHR8nRCiAKnoq4igxqY74GY6qLhqIc3XDkEq//HyKer06p6cdINJv635ADRiek2TisELAtdRsj1EFx0LoxtOtbi1RXSDUaGrzqKP6H00QWZN3adDQ4uVkgrcivXN0sPHDiQ/v37c/DgQRo3boyiKOzbt4+FCxcyatQoADZt2oSfn5/VwwohCoZXa77KsbhjBF0MYqhPGVakJeMV+gfav8Ywp9cEeszdxfnrKbz940GWvd0UJ73W1pFFIXUl+QpfHvoSgMH+gyntVtrimnO3nuPy9Xi+c1po3uDXGypbfuO1eDS5PiP0ySefsGDBAvbt28cHH3zAwIED2bdvHwsWLGD0aPNpvf79+/P7779bPawQomBQFIUJAROo6FGRaxnxjKjVFCPAnnl4hHzHwr6N8XTWE3LpBiNXH0NVZU0y8fipqsqEPRNIzUrFr4QfL9V4yeKap6ISmb/tPAN1a6jIFXArBR0/tUJa8ageaR6hV199ld27dxMXF0dcXBy7d++mV69e2fudnZ2zL5MJIcS9uDm4MaP1DJx1zuxOusD8ht3MOzaOoFLMNua92hCtRmHN4Ui+2XHBtmFFofTHhT/YFbkLvUZPYEAgGsWyqfeyjCaGrzpKNTWcd3V/mDd2mQ7ORSwPKx6ZTKgohLCZakWrMbbZWAC+iQ9hR92ugAq/9qO580XGdfUFYOrGUP46ec2GSUVhE5sWy9T9UwF4t/67VPasbHHNxXsiOHE5jumOC9BihFrdoFZXi+sKy0gjJISwqWcqP8PLNcxrkY3MDONylVaQlQY/v0zvmvBqk/KoKgxadpjTV5NsnFYUFlP3TSUhI4EaRWvwep3XLa4Xkw6ztpyjn3Y9tbkATp7QebrlQYXFpBESQtjcR40/oq53XRIzExnq6UBGyTqQEo3y04sEdixL08pepGQaeWvJfuJSMm0dVxRwWyO2siF8AxpFw/jm49Fr9BbVU1WVZec1lMy6wjC9ecV6npoE7iWtkFZYKkeNUGJiYl7nEEIUYg5aB75o9QVFHItwKv40k32bg7sPxJxGv7I381+uS3kvFy7FpfHu0oNkZplsHVkUUEmZSXy6x3zzct/afaldrLbFNVcejORsosI0h4U4kAmVW0ODVy2uK6wjR41Q0aJFiY6OBqBt27bcuHEjLzMJIQqh0m6lmfrkVBQUVoVvYE3r98DBHcJ3UvSvD1nYxx83Rx17w+IYt+6EjCQTeWLmwZlEp0VT3r08A+oPsLjetcR0pmw6w8varTRRToLeBZ6ZBRbORSSsJ0eNkJubG7GxsQBs27YNg8GQp6GEEIVTQJkABjQw//H57NQiQjt/BooWji6j+qm5fPlyAxQFftkXwZLdF22cVhQ0+6/uZ+WZlQAEBgTipLNs9LOqqoxZexyX9Gg+0f9k3tj2E/CqZGlUYUU5mlCxffv2tGnThlq1agHQo0cPHBzuvSjc33//bb10QohC5+16b3Pk+hH+ifyHIeeXsbzTJDzWD4ftU2jXvQIjnm7C5A2hTPjjJFWKu9GimretI4sCID0rncDgQACer/48jUs1trjmhuNX2XzyKgscFuFGGiafhmia9Le4rrCuHJ0RWrp0KYGBgTRq1AiA2rVrU79+/Xt+CCGEJTSKhilPTsHH1YfLyZcZnXQCU/Mh5p3rBvJ22Us851cGo0llwE8HCYtJsW1gUSDMOzKPiKQISjiXYKj/UIvr3UjNZOxvx+ms2UsHzQFMaDF2mQUamSU9v8nRGSFnZ2f69zd3sQcOHGDq1KkUKVIkL3MJIQoxT0dPZrSZQe/1vdl2eRvf+33AW3V6wvFVKCv6MLnvesJii3A44gb9Fu9nzYDmeDpbNrJHFF4nYk+w5MQSAD5p+gnuDu4W1/z0z1MYkuP4zHkxqHCmVFeqlPC1uK6wvlwPn9+6dWt2E6SqqtywKITIE7WL1WZUE/P6hXNCvmJvkzegfDPISMBx+csseK4cpT2duHA9hYG/HCbLKCPJRO4ZTAYCgwMxqkaervg0bcq3sbjmjjPX+fXgZcbol1JUTUD1rsHZkjJxYn71SPMILVmyhLp16+Ls7IyzszP16tXjxx9/tHY2IUQh17NaT56t8iwm1cTHwZ9w7dkvwasKJFzC+7feLHzFFye9hh1nrjN5Q6it4wo7tPjEYkLjQvF09GT4E8MtrpeSkcWoNcdoqTnC89odgIKxyyxMFs5FJPJOrhuhGTNm8O6779K5c2dWrFjB8uXLefrpp+nfvz8zZ87Mi4xCiEJKURRGNx1NjaI1iEuPY9jeTzG88gu4FIOoEGoHD+GL5+sC8N0/YazYf8nGiYU9CUsIY37IfACGNx6Ot7PlN95P33yauPh4pjp8b97QpD9qWctvvBZ5J9eN0Jw5c5g/fz5Tp06lW7duPPvss0ybNo158+Yxe/bsvMgohCjEnHXOzGg9A3e9OyHXQ5gRthZeWQZaRzizgS6RXzKobVUARq89xv7wONsGFnbBpJoIDA4k05RJc5/mPFP5GYtrHoqIZ1FwOB/pllOa6+BZ3jxcXuRruW6EoqKiCAgIuGt7QEAAUVFRVgklhBC3K+9Rnk9bmGf7XXpqKRuNcfDct+ad+75lkNtfdK5bCoNRZeDPcr+QeLiVp1dyKPoQzjpnxjYbi2LhBIcZWUaG/3oUP87QV7fZvLHrLHB0szysyFO5boSqVq3KihUr7tq+fPlyqlWrZpVQQgjxX23Lt6VfnX4AjNs1jgtl6kGHiQBoNo9mZr1LFHXRczUxnX1hclZI3N/VlKvMODgDgEENB+Hj5mNxzXlbz3MxOp7pjgvRoEL9XlC1ncV1Rd7L0fD5240fP56XXnqJHTt20Lx5cxRF4Z9//mHLli33bJCEEMJa3vd7n2Mxx9h3dR9Dtg3hl84/4xIfDge+w/G3/vSrOJPpJz3481gUAVVlokVxN1VVmbhnIqlZqTQo3oCXa7xscc3TV5OYt+0c7+t+ozKXwbU4PPWZFdKKxyHXZ4R69uzJ3r178fb2Zu3ataxevRpvb2/27dtHjx498iKjEEIAoNPomNpyKsWdi3Mh4QKBu8ejPj0VqnWErDTejhxFOeUam05cxWiSqT3E3daHrWfH5R3oNXrGB4xHa+EEh0aTyserjlLZdJH3dL+ZN3b+HFy8rJBWPA65PiME4O/vz9KlS62dRQghHsrb2ZsvWn/BmxvfZEP4BuqXqM+rz/8AP3TC4epRFjlO55nkiewLi6NZlWK2jivykbj0OKbumwrAO/XeoXKRyhbX/GFXGMcuxfGb0wJ0GKHmM+Db3eK64vF5pHmEhBDClvxK+DG0kXkZhOn7pxOScA56rQD30lQhkjG6paw/JoM3xJ2m7ptKfEY81YpW4806b1pcLyI2lS82n+EN7Qbqch4cPaHzdFlZ3s5IIySEsEuv1XqNjhU6kqVm8eH2D4nVO0CPr1FR6KX7m/Rjv8nlMZFtx+UdrA9bj0bRMCFgAnqtZRMcqqrKqDXH8M66wscOv5o3dpwIHqWtkFY8TtIICSHskqIoTGg+gYoeFYlOjWb4juEYKz6Jqdn7AIzKmseRkydtnFLkB8mZyUzYPQGA3rV6U8e7jsU1Vx68zD/nrjNNvxBHNQMqPgkN+1hcVzx+0ggJIeyWq96VWW1m4axzZu/VvcwNmYu23VguOVWnqJKM58YPwCRzChV2sw7N4lrqNcq6leU9v/csrhedmM6nf5zkBe12mmlOgM4Zun4pl8TsVK4aoaysLHQ6HcePH8+rPEIIkStVilQhsFkgAAuOLWBbVDCRbWeTqjpSJfkApuA5tg0obOrgtYMsP70cgMCAQJx1zhbXHPvbCRzTrzPO4SfzhjajoFgVi+sK28hVI6TT6ahQoQJGozGv8gghRK51rtyZXjV7AfDJrk+oVqcWU3ndvPPviXDlsO3CCZvJMGYQGBwImBfwbVK6icU1NxyLYuOJq0x0WIybmgI+ftB0gMV1he3k+tLYJ598wsiRI4mLk5lbhRD5x7BGw6jsWZmEjASWnfmJpFqvsMHYGI3JAKvegswUW0cUj9nXR74mPDGc4s7Fs0cZWiIh1cDYdSd4WrOPpzX7QKODbl+B9pFmohH5RK4bodmzZ7Nz5058fHyoUaMGDRs2vONDCCFsQa/V814D8/0fS04s4claroww/I9ovCD2HGwcYeOE4nEKjQvlh+M/ADC66Wg8HDwsrvnZ+pNkJMUyyXGReUOLIVDK8huvhW3luo3t3r17HsQQQgjLta/QnlpetTgVd4rT6b9hdKzHoMx3+dlhEsqhJVC1Pfg+a+uYIo9lmbIYu2ssRtVIhwodaFfe8jW//jkbw4oDl5mm/wkv9QZ4V4eWH1keVthcrhuhcePG5UUOIYSwmEbRMNBvIAO2DODXs8t5sqY/G47UJrjUazS/+iOs+wDKNALPMraOKvLQkpNLOBV3Cg8HD0Y1GWVxvdTMLEauOUpzzTFe1G4HFOg2B3SOlocVNvfIw+cPHjzI0qVL+emnnzh8WG5EFELkDy3KtMCvhB8ZxgyMnn8BMDLuGdTSDSD9Bqx5B0wy4KOguph4kXkh8wD4qPFHeDtbvvjuF5vPEBMXz+cO35k3PPE/KN/U4roif8h1IxQdHU3btm1p3LgxH3zwAe+//z7+/v60a9eO69ev50VGIYTIMUVRGOg3EIB9MRtwdblBRKKRkwEzQO8C4TsheLaNU4q8YFJNBAYHkmHMoFnpZjxbxfLLoIcj4vlhVxgf6lbiQzR4loN2Y62QVuQXuW6EBg4cSGJiIidOnCAuLo74+HiOHz9OYmIiH3zwQV5kFEKIXGlcqjEBPgEY1Sx8Ku0EYG2EM3QyL7jJ359C5CEbJhR54dczv3Lg2gGcdc6MCxiHYuEEh5lZJkasOkY9zvGmbqN54zOzwNHd8rAi38h1I7Rx40bmz59PrVq1srf5+voyd+5cNmzYYNVw1pSamkqFChUYNmyYraMIIR6DW2eFrpmC0ThcY/2xq6gNXjPfLG3KMg+pz0i2cUphLVdTrjLz4EwAPvD7gDJult8HNn/beS5ci2e64wI0qFDvZajW3uK6In/JdSNkMpnQ6+9erE6v12PKx1PZf/bZZzRpYvlkWkII+1DHuw7tyrdDRcWl5F9E3kjjaGSieSkEjzIQd16G1BcQqqry2Z7PSDYkU8+7Hq/UfMXimmeuJfHV1rMM0P5GVS6Bizc8PdkKaUV+k+tGqG3btgwaNIgrV65kb4uMjGTIkCG0a2f5EMW8cPbsWUJDQ+ncubOtowghHqP3G7yPgoLidgyN02XWH4sC56Lw3LeAAod/hBNrbR1TWGhT+Ca2Xd6GTqNjfMB4tBqtRfWMJpXhq45S0XSJgfrfzBs7TwMXLyukFflNrhuhr776iqSkJCpWrEiVKlWoWrUqlSpVIikpiTlzcr+mz44dO+jatSs+Pj4oisLatWvvOmbevHlUqlQJJycn/P392blzZ66eY9iwYUyeLJ28EIVN1aJV6VzZ/A8gx+Kb+fNYFKqqQsUW5snwAH7/ABIu2zClsMSN9BtM3mf+/f523bepWrSqxTUXB4dzJCKO6Q4L0JEF1TtB7ecsrivyp1zPI1SuXDkOHTpEUFAQoaGhqKqKr68v7ds/2nXTlJQU6tevzxtvvEHPnj3v2r98+XIGDx7MvHnzaN68Od988w2dOnXi5MmTlC9fHgB/f38yMjLueuzmzZvZv38/1atXp3r16gQHBz9SRiGE/RpQfwAbwzaB2xmiYk5xPNKfumU9zQtlXtgGVw7B6neg7zqw8EyCePym7Z9GXHocVYtU5a26b1lc71JcKp9vOk1f7SbqK2fB0QO6fCEryxdguWqEsrKycHJyIiQkhA4dOtChQweLA3Tq1IlOnTrdd/+MGTPo168fb71l/gGfNWsWmzZtYv78+dlneQ4ePHjfx+/Zs4dly5axcuVKkpOTMRgMeHh4MHbsvYc/ZmRk3NFUJSYmAmAwGDAYDLl+ffdzq5Y1az5O9pzfnrODfee3RfbSzqV5tko3Vp9bjUOJjawLaUXNki7mnc9+jW5hG5SL/2DcMQNT88EPrCXvve3cK/+uK7v4/cLvKCiMeWIMmMBgevTXp6oqI1YdpVhWFMOdVoAKxrZjMbmUAAvet4L43tuDnOZVVFVVc1O4SpUqrF69mvr16z9SsAeGURTWrFmTvYxHZmYmLi4urFy5kh49emQfN2jQIEJCQti+fXuu6i9atIjjx48zffr0+x4TGBjI+PHj79r+888/4+LikqvnE0LkDwmmBL5ImIlJyUIf9QZja1bJ/gd++dgd+EUsxISWndXHcMO1sm3DihzJUDOYnTibBDWBAMcAOjtbfg/ovmiFn85rWOowmRaa48S41WRX1RGgPPLcw8KGUlNT6dWrFwkJCXh43H+tuVxfGru1+vzSpUvx8srbG8diYmIwGo2ULFnyju0lS5bk6tWrefKcI0eOZOjQf1cpTkxMpFy5cnTs2PGBb2RuGQwGgoKC6NChwz1H4eV39pzfnrODfee3ZfaL+y6z4twvpBcJokKDPtQp42neoXbCtOY6mlO/0fL6YrKe3QoObvesIe+97fw3/9QDU0lISKCMaxk+7/I5zjpni+rHJGcwdvYuntduoYXmOKrOCc/ei+nsVcXq2e2Nvea/dUXnYXLdCM2ePZtz587h4+NDhQoVcHV1vWP/oUPWn6Tsv5Niqar6SBNlvf766w89xtHREUfHu9eP0ev1efIDkFd1Hxd7zm/P2cG+89si+4CG7/DrudXgfJnvQv7kq4p9/93Z7UuIPIgSH4Y+6BPoPveBteS9tx29Xs/x+OOsOLMCgHEB4/BwtvwfqZ+uP4ZDWgzjnH8CFZTWI9GXrGlx3dsVhPfenvLnNGu+Xn3e29sbrVZ719mf6Ojou84SCSHEgxRzLkbLks+x7dov/BO7lCzjq+i0N38F3hpSv/gZCFlqnjSvdo8HFxQ2kWHMYFzwOFRUulftTjOfZhbX3HTiKn8ei2Kew2Lc1WQoXR+avW+FtMIe5PpmaYA333yTcuXK5Umg2zk4OODv709QUNAd9wgFBQXx7LOWryEjhChcRjV/l60r12LUXeW7kDW84//CvzsrNocWQ2HndPh9kHmV+iJ5/3tO5M53x78jLCEMb2dvhjWyfKWAhDQDY9Ye5ynNfjpr9oKihW5fgTbX5wmEncrVHWA6nY7p06djNFpv5ebk5GRCQkIICQkBICwsjJCQECIiIgAYOnQoCxcu5Pvvv+fUqVMMGTKEiIgI+vfvb7UMQojCobR7USpozTfVLj71zd0jjFqPMDdA6Qmw+m1ZpT6fuWq8yqKTiwAY1WQUno6eFtecvP4U6UlxfOZorkvzQVC6nsV1hf3I9a3w7dq1Y9u2bVYLcODAAfz8/PDz8wPMjY+fn1/28PaXXnqJWbNmMWHCBBo0aMCOHTtYv349FSpUsFoGIUTh0bdOb0xZbiQZr7Hm7Jo7d2r10HOB+WbpiGD4Z4ZtQoq7ZJmyWJO6hiw1i/bl29OhguXTtwSfi2HZ/kuM1P2MtxoPxapCq+FWSCvsSa7P/XXq1ImRI0dy/Phx/P3977pZulu3brmq17p1ax42gn/AgAEMGDAgt1GFEOIunWqXZ9zfbdGUWMfcw1/TrUo3nHRO/x7gVRk6fw5r34Wtk6FyGyjbyHaBBQC/nP6FSGMk7np3RjUZZXG9tEwjI1Yfo5nmBK/otpo3dpsDeqcHP1AUOLluhN59913APNHhfymKYtXLZkIIYW3uTnqalXiGvYbtxHGd5aeX07d23zsPqv8KnA2CE6thVT/o/w84utsmsOBS4iXmH50PwJCGQyjuUtzimjP/OkN0XDw/Oy00b2j8FlQIsLiusD+PtPr8/T6kCRJC2INn6pYjM8a8SPR3x74jxZBy5wGKAs/MBM9yEB8O6z9+/CEFYJ4uZfzu8aQb06msq8yzlS0fKHPk0g0W7rzAUN2vlOUaeJSBduOskFbYI5kuUwhR6LT3LYmS1BhThjfxGfEsPbn07oOci5iH1CsaOPIzHF/12HMKWHtuLXuv7sVJ68Szzs8+0hxyt8vMMjF81VHqcJ63dBvMG5+ZCU7WmzBX2JccN0KdO3cmISEh++vPPvuMGzduZH8dGxuLr6+vVcMJIURe8HDS82S1kmTEmBeLXnRiEQkZCXcfWCEAnrw5RPv3IZBw6TGmFDFpMXx+4HMA+tfrTzFtMYtrfrP9POevxjPdcQEaTFD3Baj+lMV1hf3KcSO0adOmOxYjnTp1KnFxcdlfZ2Vlcfr0aeumE0KIPNKpbmmyEuuhy/Ih2ZDMD8d/uPeBrYZD2caQkYD2t3dBNT3eoIXYpL2TSMpMwreYL71q9LK43rnoJOb8fY53tL9TnQhwKQZPT7FCUmHPctwI/XdkVy7XahVCiHylQ62S6LVaEqPMZ4V+Dv2ZmLSYuw/U6uC5BeDgjubSHqpfW/eYkxZOWyK2EHQxCK2iZXzAeHQayyY4NJlUhq86RjnTJQbp15o3Pj0VXL0tDyvsmtwjJIQolDxd9DSv6o0xuRbF9dVIy0pjwdEF9z7YqxJ0mQ5Ajai1KJEHH2PSwicpM4lJeyYB8EadN6jpZfmaXz/uucjhi7FMd1iAHgNUewrqPm9xXWH/ctwIKYpy101qlt60JoQQttS5bmlAwRT3NAArz6wkKjnq3gfXewlT7efQYEK79h3ISHp8QQuZmQdnEp0WTQWPCrxT7x2L612OT2XqxlB6a4PwU86Agzs8M8M8OlAUejk+16iqKq+//nr2yuzp6en0798/e0LF2+8fEkIIe9DRtySjNArhl8sQ0MKfY7EH+fro14wPGH/3wYqC8enPST+zHZcb4bBhOHSf99gzF3QHrh5g5ZmVAIxrNu7OyS4fgaqqjF5znKKZVxnpvBxUoEMgeJa1PKwoEHJ8Rqhv376UKFECT09PPD09ee211/Dx8cn+ukSJEvTp0ycvswohhFUVcXEgoKr5HpHKWvNlkt/O/UZ4Qvi9H+DkycGK/VEVDYT8BMdXP6akhUOGMYPxu81N6PPVn6dxqcYW11xzOJLtZ6KZ7PA9Tmo6lA8A/zctrisKjhyfEfrhh/uMqBBCCDvWpW4pdpy5zqEznrSq04rtl7czL2Qe01pNu+fxcW41MAUMRrtrBvwxGMo9IWcXrOSbI98QnhhOcefiDPEfYnG9mOQMJvxxkh6af2ipOQJaR+g2GzRye6z4l/w0CCEKtQ6+pdBqFE5GJfJcxX4AbAjfwOm4+08HYnryIyjjf3OV+ndklXorOB13OnsKg9FNR+PhYPkEh4HrTqBNjWG8480JM1sPB+9qFtcVBYs0QkKIQs3L1YGAKuaJ+k5FuPNURfPkel8d/ur+D9LqzUPq9a5w8R/Y9eXjiFpgZZmyGBc8jiw1iw4VOtCufDuLawadvMYfR6MYr1+Ch5oEpepCwAdWSCsKGmmEhBCFnnn0GGw4HsV7Dd5Do2jYdnkbR64fuf+DilWBzjcvn239DCIPPYakBdNPp37iROwJ3B3cGfnESIvrJaYb+GTtMdprDvKMdjcoWuj2lbmBFeI/pBESQhR6HX1LotUoHI9MRJtVkm5VugEw59CcBz+wwavg+yyYsmDVW5CZ8uDjxV0uJV3KPvs2rNEwq6wsP2VDKKmJ8Ux2vHlva8D74NPA4rqiYJJGSAhR6BVzc6RpZS8A1h+Pon/9/ug0OvZe3cveqL33f6CiwDOzzKuXx52HjZafzShMVFVlwu4JpBvTeaLUE/So2sPimnsuxPLz3ghG6H6huBoHXpWhtXxfxP1JIySEEECnOubLY+uPRVHGrQwvVH8BgNmHZz94SSEXL+jxNaDAocVw6vfHkLZg+O38b+yJ2oOj1pFxzcZZPElvusHIiFVHaaKc4lXdFvPGbnNA72yFtKKgkkZICCGAp+uUQqPA0csJXIpL5e16b+OkdeLo9aNsv7z9wQ+u1BKaDzJ/vm4gJF7J+8B2LiYths/3m1eWH9BgAOU9yltcc+ZfZ4iKvcF0x5tLpfi/ARVbWFxXFGzSCAkhBODt5kiTSubRYxuOR+Ht7M0rtV4BYM7hOZgetup8m9FQuj6kxcOa/mCSVeofZMq+KSRmJlLLqxZ9fC2fjPfY5QQW7gxjiG4V5bgK7qWhwz1mCBfiP6QREkKImzrXLQXAn8euAvBm7Tdx07txJv4Mm8M3P/jBOgfo+R3oXSBsO+yZm9dx7dbWiK1sCt+EVtESGBBo8cryBqOJj1cdpZZ6nv/p/jRvfGYmOHlaIa0o6KQREkKIm56qUwpFgSOXbnA5PpUiTkXoU9t8tmJuyFyyTFkPLuBdDZ6ebP78r/EQdTSPE9uf5MxkPt37KQB9avfBt5ivxTW/3XGBs1FxfOG4AC0mqP0c1OhkcV1ROEgjJIQQN5Vwd+KJiubRYxuPm88K9a7VmyKORQhPDOePsD8eXqRhX6j5DJgMN4fUp+ZlZLsz69AsolOjKedejgH1B1hc7/z1ZL7ccpa3tX9Sg4vgXBQ63Xt5FCHuRRohIYS4za3JFf88FgWAm4Mbb9V9C4Bvj31LlvqQs0KKAl1ng1spiDkNmz/J07z25NC1Qyw/vRyAwGaBFq8sbzKpjFh1lLLGywzW31wA9+kp4Gb5XESi8JBGSAghbvP0zctjhyNucOVGGgAv1XiJEs4luJp6lf2Z+x9exLUY9Jhv/vzAd3B6Qx4mtg8ZxgzGBY8D4Llqz/FE6ScsrvnT3oscCI/lc4eFOGCAKu2g3ksW1xWFizRCQghxm5IeTjSqUBSADTcvjznpnHin/jsAbEnbQkxazMMLVWkLzd43f/7be5B0LU/y2otvj35LeGI43s7eDPUfanG9yBtpTNkQyqvaLfgroeZ137rOMp+REyIXpBESQoj/uHV5bP3Ny2NgPotRy6sW6aQz/eD0nBVqNxZK1oXUWFj7bqEdUn8m/gzfH/segFFNRuHpaNloLlVV+WTNMTwzrzHaYZl5Y/txUMTyuYhE4SONkBBC/MetWaYPXoznakI6ADqNjk+e+AQFhc0Rm9lxecfDC+kcoedC0DnB+S2w79u8jJ0vGU1GAoMDyVKzaFe+HR0qdLC45rojV9h6OppJDj/grKZBuSbQ+C0rpBWFkTRCQgjxH6U8nfDPvjz271mhWl61CHAMAODTPZ+SasjBiLASNaGjebg4QWPh2gmr583Pfg79mWMxx3DTuzGqySiL68WmZBK47gTdNMG01hwGrYN5GQ2N1gppRWEkjZAQQtzDrctjG25OrnhLO6d2lHYtTVRKFF+FfJWzYo3fgmpPgTHDPKTekGbtuPnS5aTLzDk8B4ChjYZSwqWExTU/Wx+KkhrLRMcl5g0tP4biNSyuKwovaYSEEOIeOtUxzzK9/2Ic0Ynp2dsdFAdGNTaf2fjp1E+ciMnBGR5FgWfngmsJiD4JfwXmReR8RVVVJu6ZSFpWGo1KNqJntZ4W1zwRr/D70auM0y/BU02CErX/XeNNiEckjZAQQtyDTxFn/MoXQVX/HT12S3Of5nSq1AmTaiJwd+DDZ5wG89w23W8Oqd/7NZwNyoPU+ccfF/4g+EowDhoHxjUbh0ax7M9NUnoWKy5oaKM5zLPaYFA08Owc89ImQlhAGiEhhLiPLvcYPXbLx40/xsPBg9C4UJaeXJqzgtXaQ5P+5s/XDoDk69aKmq/EpsUydf9UAN5t8C4VPStaXHN60BmyMtOY6mgefUbTAVDG3+K6QkgjJIQQ9/H0zctj+8LjiE5Kv2Oft7M3wxoNA8zrkF1Oupyzou3HQwlfSImGde+Dqlo1c34wdf9UEjISqFG0Bn1r97W43r6wOH7ed5mPdcspocZC0YrQZrTlQYVAGiEhhLivskVdqF/OfHls04m7J0TsXrU7jUs1Jt2Yzqd7PkXNSVOjdzIPqdc6wpmNsH9hHiS3nR2Xd7AhbAMaRcP4gPHoNXqL6qUbjIxYdZTGSih9dDcvJ3adDQ4uVkgrhDRCQgjxQF3qms8KrT969+UxRVEY23QsDhoHdl3Zxfqw9TkrWrI2dBhv/nzzJxAdaq24NpViSGHC7gkA9PHtQ23v2hbX/Orvc0TGxDPd0dwwmuq/CpVbWVxXiFukERJCiAe4Nbni3rBYYpMz7tpf0bMib9d7G4Bp+6eRkJGQs8JN+kPV9pCVbh5Sn3V3bXvz5aEvuZZ6jbJuZRnQwPKV5U9FJfL19vMM1q2iAldI1xXB2H6CFZIK8S9phIQQ4gHKeblQr6wnJhU2n4q+5zFv1nmTKp5ViEuP44sDX+SssKLAs/PApRhcOwZb7PsPfEh0CMtCzctdjAsYh7PO2aJ6WUYTw1cdpbZ6lnd0fwJwpFxfcLJseQ4h/ksaISGEeIhbZ4U2Hr/3wql6rZ5xAeaV1decW8O+qH05K+xe0jy/EMDur+D83xZntQWD0cC44HGoqHSv2p2mpZtaXHNRcDinL1/nC8dv0WDCVLsnV4vIKDFhfdIICSHEQ9waRr83PJ5kw72P8Svhx4vVXwRgwp4JZBhzeKmrRido1M/8+Zp3ISXW0riP3cbwjVxIuICXk1f2SDpLRMSmMn3zaQbpVlOVy+BaAmPHyVZIKsTdpBESQoiHKF/MhTplPDCaVA7FKPc9bpD/IIo7F+di4kW+PZqLBVY7fgreNSD5Khz43gqJH69fQn8B4NVar1plZflRa45RPess/XV/mDc+MxNcvCyNKcQ9SSMkhBA5cOvy2KpwLX0XHWDLqWuYTHcOl/dw8GBkk5EAfH/se87Gn81ZcQcXaPae+fMzG62W+XE4ev0ox2KOodforbKMxq8HL7P/3BW+cPgGDSao8zzUesYKSYW4N2mEhBAiB95oXpEudUqhoBJ8Po5+iw/QbsZ2Fu0KIznj3yU22pdvT+tyrclSsxi/ezwm1ZSzJ6jW0fzfyIN2NeP0T6d+AqBTpU4Ucy5mUa3rSRl8+ucpPtCtpppyGVyLQ+fPrRFTiPuSRkgIIXLAxUHHrJfqMcbPSL/mFXB30hEWk0Lg7ydpNmkLE/84yaW4VBRFYXST0bjoXDhy/QgrT6/M2RN4lIbS9QEVztnHOmTXU6+zOXwzAL1q9bK4XuDvJ6iQHiqXxMRjJY2QEELkQjEnGPF0DfaMbMfEZ2tT2duVpIwsvvsnjFafb+XtJQcIv6bnA78PAJh1aBbXUu492uwu1Z4y//fMpjxKb10rz6wkS83Cr4QftYtZNnli0MlrBB2NYLr+G7SYoE5PqNXVSkmFuD9phIQQ4hG4Ouro3awifw1txQ9vNObJat7muYZOXuPlb/fwY1BZfJyrk2xIZsq+KTkrWv1p83/P/w3G+wxPyycyjZmsOL0CgF41LTsblJhuYMza43ygW011zc1LYp3kkph4PKQREkIIC2g0Cm1qlODHfk0IGtKSXk3K46TXEBqVzNkTnUDV8FfEX6wOzcFN0D5+5iYgIxEidud9eAtsCt9EbHosJZxL0K5CO4tqTd0QSvGkk7yr+928ocsMcLXsfiMhckoaISGEsJJqJd2Z1KMue0a2Y/jTNSnpVImM2JYAjP1nIgOX7ebY5QcswaHR/HvTdD6/PPbzqZ8BeKnmSxYtrLovLI6Ve88zXf/1v5fEfLtZK6YQDyWNkBBCWFkRFwfebV2FnR+3YVq7D9GbiqPoE9kctYiuX/3D8/ODWX8siizjPUaU2UEjdPT6UY7HHsdB48Dz1Z9/5Dq3VpYfqFtDDbkkJmxEGiEhhMgjOq2G7g0qMvepzwBw8NqNg+slDlyMZ8BPh2j1+Ta+3n6eG6mZ/z6oSlvQ6CD2LMSet1HyB7s1ZP7pSk/j5fToo7q++vscrrHHeFe3zrxBLokJG5BGSAgh8lgzn2Z0rdwVUKlZZxPvt6mIl6sDkTfSmLIhlGaT/2b0mmOci04CJw+o0Nz8wLObbZr7XqJTo60yZP5UVCLfbw/lc/036DBB7efkkpiwCWmEhBDiMRjWeBhFHIsQlniOIj67CR7RlmnP16NmKXfSDEZ+2htBh5k7+C0kEqrfGkaf/2aZtsaQeaNJZfiqo/TXrKam5hK4eMvEicJmpBESQojHwMvJi48afwTA10e+JjotkhcblWPDoCf55X9NaVW9OKoKo1Yf43Jx8w3WhO+CjCQbpr5TpjEze4JIS84G/bArDFPkYQbcuiT2zAxw9bZGRCFyTWfrAAWBqqpkZWVhNBpz/BiDwYBOpyM9PT1Xj8sv7Dm/PWcH+86fk+x6vR6tVvuYkz0eXSt3Zd35deyN2suEPRNY0GEBiqLQrEoxnqjkxSvf7mFfeBzvbUxgrVcVlLjzcH5rvrlklD1k3qUE7co/2pD5iNhUvtx8gpXZl8R6gO+zVk4qRM5JI2ShzMxMoqKiSE1NzdXjVFWlVKlSXLp0CUW5/2rW+ZU957fn7GDf+XOSXVEUypYti5ub22NOl/cURWFs07E8t+459kbt5fcLv9OtirnJ0WoUZr7cgE6zdnDkcgIHKj5BY86bR4/lg0ZIVdXsm6RfqvFoQ+ZvrSz/P/VXamovobp4o3Sebu2oQuSKNEIWMJlMhIWFodVq8fHxwcHBIcd/mEwmE8nJybi5uaHR2N8VSnvOb8/Zwb7zPyy7qqpcv36dy5cvU61atQJ5Zqi8R3n61+/Pl4e+5PP9n9OiTIvskVdlijgzpWc9Bvx0iFkRlfjJAfMN0yaTeY4hGzoac5QTsScsGjL/68HLxJ/fzwAH8yUxpcsXcklM2Jw0QhbIzMzEZDJRrlw5XFxccvVYk8lEZmYmTk5OdvfHDOw7vz1nB/vOn5PsxYsXJzw8HIPBUCAbIYC+tfuyPmw9Z+PPMn3/dCY9OSl7X+e6pXm5cTlW7c8iBWdcU6Ih6jCU8bdh4jtXmX+UIfPXkzKY8sdRluq/RqeYwLc71O5u3ZBCPAL7+i2aT9nbHyMh8jN7u9z3KPQaPYHNAlFQ+P3C7wRfCb5j/9iuvpQr7sl2Y10AVBtPrhidGk1QeBDw6DdJB/5+gj5ZK6mluYTqUgy6fGHNiEI8MvkLLoQQNlCveD1eqfkKABN3TyQtKy17n4uDjtkv+7FdbQhA3OHfbZLxltuHzPsW883144NOXiP8WDDvaX8D5JKYyF+kERJCCBv5oOEHlHQpyeXky3xz5Js79tUp40m91uZ7cYolnuTChXO2iHjnKvOPcDYoMd3A+DWHma7/5rZLYj2snFKIR1coGqGwsDDatGmDr68vdevWJSUlxdaRhBACV70ro5uMBmDRiUWcjjt9x/5X2jbivENNAH5buYh0w+OfLmFT+Cbi0uMeecj8tI2hvJC2nFqaCPMlMRklJvKZQtEIvf7660yYMIGTJ0+yfft2HB0dbR0pX2vdujWDBw/O88c8qv8+13+/VlWVt99+Gy8vLxRFISQk5I5tWq2WY8eOPZasQjxMm/Jt6FChA0bVyPjd4zGa/m12NBqFko3MQ+drJe9hyobQx5rt9iHzL9d4OddD5veFxXF47w4G3H5JzK241XMKYYkCP2rsxIkT6PV6nnzySQC8vB59gcCC5PXXX2fx4sV3bT979iyrV69Gr8/dL7z/PqZ169Y0aNCAWbNmWRo118+9ceNGFi1axLZt26hcuTLe3t53bKtYsSIODg55nssePc7vm/jXiCdGsPvKbo7FHGPxycW8WefN7H1udbpA8DSe1Bzlg+CztKzuTduaJR9LrtuHzPes3jNXj003GPlk1UG+1H+NXjGaJ02US2IiH7L5GaEdO3bQtWtXfHx8UBSFtWvX3nXMvHnzqFSpEk5OTvj7+7Nz584c1z979ixubm5069aNhg0bMmnSpIc/qJB4+umniYqKuuOjUqVKeHl54e7unqtaj/IYa/nvc58/f57SpUsTEBBAqVKl0Ol099yWW5mZmQ8/yE4V5NdmD0q4lGBYo2EAzD40m5DokH93lq4PbqVwVTJ4QhPKsJVHiU5Mfyy5LBky/9Xf5+h842dqaSIwOReDzjJKTORPNm+EUlJSqF+/Pl999dU99y9fvpzBgwczevRoDh8+zJNPPkmnTp2IiIjIPsbf3586derc9XHlyhUMBgM7d+5k7ty57N69m6CgIIKCgh7Xy8vXHB0dKVWq1B0fWq32npeePvjgAz7++GO8vLwoVaoU48ePv6PW7Y95/fXX2b59O19++SWKoqAoCuHh4aiqyrRp06hcuTLOzs7Ur1+fX3/99YEZU1JS6NOnD25ubpQuXZovvrj7l+l/n3vgwIFERESgKAoVK1a8a1vlypUBHpqndevWvP/++wwdOhRvb286dOiQo8fd7z0LDAzM3m8ymZg6dSpVq1bF0dGR8uXL89lnn2Xvz+179fvvv1OkSBFMJhMAISEhKIrCRx99lH3MO++8wyuvvHLf13a/71tO/PLLLzg5OREZGZm97a233qJevXokJCTkqEZh91y153i64tMYVSMf7/iYhIyb75uiQPWOADzvfpy4lEw+XHkEk0nN0zyWDJk/FZXI9h1bskeJabpMl0tiIt+y+aWxTp060alTp/vunzFjBv369eOtt94CYNasWWzatIn58+czefJkAA4ePHjfx5ctW5bGjRtTrlw5ADp37kxISEj2H7X/ysjIICMjI/vrxMREwLxGksFguONYg8GAqqqYTCZMJhOqqpKWw5sZVVUlLdOINsNglXlTnPXaXNVRVTU7+/32375v8eLFDBkyhN27d7N7927efPNNGjRoQLdu3bKPu/WYmTNncubMGWrXrp3dMBUvXpzRo0ezZs0a5s6dS7Vq1dixYwevvfYaxYoVo1WrVvfMMWzYMLZu3cqqVasoVaoUo0eP5uDBg9SvX/+OfLc/d+XKlVmwYAF79+5Fq9Xi4OBwx7Zb8z598sknrF279oF5Fi9eTP/+/dm5c2f2c3zyySc5eh33es+aNWtGhw4dGDFiBAsXLuSLL76gRYsWREVFERoamv2aHvQcLVu2vOt71KJFC5KSkjh48CD+/v5s27YNb29vtm/fnn3Mtm3bGDRoUPbX/31tpUuXvuf37X4/I7d78cUXmTJlCpMmTWLOnDlMmDCBTZs2ERwcjLu7+x0/I/f6+brdrf+X8uOEird+B/z3d4G1jGo8ihMxJ7iUfInRO0czo+UMc1NauT26Q0vo7HCEEfpe7Dwbw7c7ztGvecU8y77s1DKy1CwaFG9ANY9qOX6c0aQyauUBpmrNl8RMNbtirP4MWPie5fV7n5fsOTvYb/6c5rV5I/QgmZmZHDx4kBEjRtyxvWPHjgQHB9/nUXdq3Lgx165dIz4+Hk9PT3bs2ME777xz3+MnT55819kOgM2bN981e7ROp6NUqVIkJyeTmZlJWqaRZjP25CiXte0e2hRnh5z/0TAYDPz55594eHhkb2vfvj2LFi0iKyuLzMzM7CYwKysLX1/f7LMu3bt3Z86cOWzfvp02bdpkH3PrMYqioNFo0Ol02e9ZdHQ0M2fO5LfffuOJJ54A4LnnnmPbtm3MnTsXPz+/uzImJyfz/fffM3/+fJo0aQLAnDlzqF279l35bn9uvV6Poih3fL/+uy0lJYVZs2Y9ME9WVhaVKlVi9OjR2XWioqJy9Dru955t2LABX19fZs+ezbRp0+jRw3zPRPHixalXrx6JiYmkpKTk6DmSkv5dlVxRFOrWrcumTZuoVq0af/31F/3792fatGlERkaSmprKmTNnaNSoEYmJifd8bcBd37fcjLAcOXIkr7/+Ol5eXnz11VesX78ed3f37O/Txo0bGTNmDCaTiUGDBtGnT5971snMzCQtLY0dO3aQlZWV4+d/nPLyrHJXuvIN37A9cjtj1owhwCkArTGdTooOh6QI+pWKYO6lcny+6TRZkScpl8sl2XKSPUvN4ufEnwGokVKD9evX57j+1isKLa+txVd/kXStG1t1T5G5YUPuQj6APZ/Rt+fsYH/5c7oGaL5uhGJiYjAajZQseeeNgSVLluTq1as5qqHT6Zg0aRItW7ZEVVU6duzIM888c9/jR44cydChQ7O/TkxMpFy5cnTs2PGOpgEgPT2dS5cu4ebmhpOTE7pM2/3Sdvdwx8Uh599OvV5P69atmTdvXvY2V1dXPDw80Ol0ODg4ZL9enU5HvXr17nj9ZcqUISYmBnd3dxRFuedjbv/69OnTpKen89xzz92RIzMzEz8/v7veWzBPe5CZmUnbtm2z93t4eFCjRo0HPtet5Rtur3n7NlVVOXTo0EPz6HQ6nnjiiTvq5PR13O89S0hIIDIykoyMDLp06XLP1/2w53B3dycpKSn7vb+lbdu27Nmzh5EjR7Jnzx4mT57M+vXrOXr0KDdu3KBkyZI0atQoO99/X9u93svcePHFF5k2bRrTpk1j48aN2c0rmBvDsWPHsmXLFhRFoW3btvTq1euegxfS09NxdnamZcuWODk55TpHXjIYDAQFBdGhQ4dcDyjIDfcz7kw9MJXNmZt5pdUr1C5WGyX5F7iwlSF10zjjVoKgU9GsuuLB2gFNc/T/fm6y/xH2Bym7UyjhXIKh3YbmeLRYRFwqP3z1M5/r1gKg6zaT9r7WuUH6cb33ecGes4P95r/1j7CHydeN0C3/veSjqmquLgM97PLb7RwdHe85vF6v19/1A2A0GrPPfmg0Glwd9Zyc8FSOnsdkMpGUmIS7h7tVlujI7aUxRVFwc3OjevXq991/ey4HB4c7vlYUBZPJdMdx/33Mf78G+PPPPylTpswd2xwdHe/5Htx6Pbfe3wfl+2+OW4+7V61blzJzkud+i4Pm5HX89z3TaDSoqoqrq+t9X1dOnuPWa/nve9CmTRu+//57jh07hkajoU6dOrRq1YqdO3cSHx9Pq1at7jj+fq/tXt+3nNi0aROhoaEYjUZKly59R40DBw5Qu3ZtypYtS2JiIp06dSIoKCj7nqXbaTSa7DN7+fWXbl5ne9X3VQ5dP0TQxSBG7BrBiq4r8KjRCS5sRXdhC9NeeI9OX+4kLDaVSRvOMvX5elbLrqoqy88sB+Dlmi/j4pizdRRVVWXCuuNMUuajV4yotbqiq/eC+R4nK8rPPxcPY8/Zwf7y5zRrvm6EvL290Wq1d539iY6OvussUX6gKEqOz8qYTCayHLS4OOgK5FplDg4OGI3/3i/l6+uLo6MjERER970f6L+qVq2KXq9nz549lC9fHoD4+HjOnDmT4xr3U6NGjVzngUd7Hf9VrVo1nJ2d2bJlS/a9b7l5jvvdW9OyZUuSkpKYNWsWrVq1QlEUWrVqxeTJk4mPj2fQoEEPzfbf71tOHTp0iBdeeIFvvvmGZcuWMWbMGFauXJm9/8qVK3c0dWXLlr3jxmpxJ0VRCAwI5GTsSSKTIxm3axwz6g1EAbgYTFFNKjNeqs+rC/ey/MAlWlYvTpd6pa3y3I86ZH7VoUjqh3+Pr/4iRqeiaLvMsHoTJEReyNeNkIODA/7+/gQFBWXfSwHm65TPPvusDZOJh6lYsSJ79+4lPDwcNzc3vLy8GDZsGEOGDMFkMtGiRQsSExMJDg7Gzc2Nvn373lXDzc2Nfv368dFHH1GsWDFKlizJ6NGjrdI4uru78+GHH+Yqz63H5fZ1/JeTkxPDhw/n448/xsHBgebNm3P9+nVOnDhBv379HvocvXv3vmddT09PGjRowNKlS/nyyy8Bc3P0wgsvYDAYaN269UOz3ev7ptFo+Oqrr1izZg1btmy56zHh4eF06dKFESNG0Lt3b3x9fWncuHH2jdvw703StysMi6tawsPBg+mtptN7Q2/+iviLX0o1ppd3DYg5Def/JqDOcwxoXYW5W88zcvVRGpQvQpkizhY/b26HzKuqyrojV1j2+5/8olsDgLbLdHArYXEWIR4HmzdCycnJnDv37xo6YWFhhISE4OXlRfny5Rk6dCi9e/emUaNGNGvWjG+//ZaIiAj69+9vw9TiYYYNG0bfvn3x9fUlLS2NsLAwJk6cSIkSJZg8eTIXLlygSJEiNGzYkFGjRt23zueff05ycjLdunXLbl6sNRx7woQJlCxZMld5gEd6Hf81ZswYdDodY8eO5cqVK5QuXfqOn+lHfY42bdpw6NCh7KanaNGi+Pr6cuXKFWrVqvXQXPf6vlWsWJGYmBjOnz9/1/FxcXF06tSJbt26ZWfz9/ena9eujB49mo0bNwLm+6NuPwN0+fJlmjZt+tA8hV0d7zoM9R/KtP3TmH5gOg0qBeAbcxrObII6zzG4fXV2nYsl5NINBi87zLK3m6HVPHqDmdsh88cjEwhcd4LDF2NY5zAXvcY8SkxTJ3eTLwphU6qNbd26VQXu+ujbt2/2MXPnzlUrVKigOjg4qA0bNlS3b9/+2PIlJCSogJqQkHDXvrS0NPXkyZNqWlparusajUY1Pj5eNRqN1oj52NlzfnvOrqr2md9gMKhVq1ZVIyIi1IiICLVq1apqTEzMPY+15P+rvJaZmamuXbtWzczMfGzPaTKZ1IFbBqp1FtVROy1royYFeqrq1EqqasxSVVVVL8akqLXHblQrDP9D/fKvM/etk5Pscw7NUessqqP2Wd/ngZmuJ6Wrw389olYc8YdaYfgf6ogxw1V1nIdqmlJBVZOuPcrLfChbvPfWYs/ZVdV+8z/o7/ftbH5zSuvWrbPntLn9Y9GiRdnHDBgwgPDwcDIyMjh48GD2PCpCCPug0+n44osvaNeuHa1ateLDDz+kWLFito5lFxRFYWLziZR2Lc2l9OuML1kSNTUWIs3zp5Uv5sLE7rUB+HLLWQ5ejHuk58k0ZrLyjPm+rvudDTIYTXz3Txhtpm9j2f5LqCp0r1+SiV6bzFlbDJFLYsLu2LwREkIUDt26dSM0NJRDhw7x9ttv2zqOXfF09OTzVp+jU3RsdHZgpbub+fLYTT38ytK9gQ9Gk8oHv4SQmJ77ie9urTJf0qUkbcu3vWv/jjPX6fTlTib+cZKk9CzqlPHg1/7NmFU7DN2NC+DsBY36WfQ6hbAFaYSEEMIO1C9enw8afgDAVK+inD575ySHE7vXoZyXM5E30hi95vg9b1C/H1VVWXpqKQAv1XjpjnmDLsam8NbiA/T5fh/nopMp5urAlOfq8tt7LWhUvgjsnG4+sNkAcMzl7I5C5APSCAkhhJ3oW7svT5ZqSqZGYZg2ntTYfweauDvp+fJlP7Qahd+PXGHVoZxPT3Dk+hFOxp68Y8h8SkYWUzeG0mHGDv46dQ2dRuHN5pX4e1hrXn6ivPmm7FPr4HooOHnCE3KWT9gnaYSEEMJOaBQNn7WaRglVQ7iDnok7R95x5qdh+aIM7WCeJHXsb8cJj8nZEik/h5qX0+hcuTNFHIqy+tBl2kzfxvxt58k0mniymjcbBz/J2K6+eDrfPFukqrDj5tmgJv3NzZAQdkgaISGEsCNFnYryuU9HtKrKHwmhrD239o79/VtVoWllL1IzjXyw7DCZWQ9eNPf2IfONinal59fBDF1xhOikDCoUc2FBn0YsefMJqpZwv/OBpzfAtWPg4GZuhISwU9IICSGEnWlYry/vx5vn05q09zPOxf97iUyrUZj5UgM8nfUcvZzAjKAzD6y14vQKstQsimqqM/jH6xyOuIGLg5aPn67B5iEt6eBb8u7JL1UVdkwzf/7E/8Dl4RMvCpFfSSMkhBD2pmRt3lTdCUhNI92YwbDtw0g1/LvSdmlPZ6b2rAvANzvOs+tczD3LJGeks+T4MgCuRDRCVeE5vzJsHdaaAa2r4qjT3vv5z22BK4dB7wLN3rfuaxPiMZNGSAgh7I2ioKn+FJOux1Jc48j5hPNM3jf5jkOerlOaV54oj6rCkOUhxKVk3rF/6+loOi6YTZopAZPBk1qeAax6N4AZLzWgpIfT/Z/79rNBjd4EV29rvzohHitphIQQwh5Ve4piJhNTb6SjUTSsPbeW38//fschY5/xpUpxV6KTMhi19gSqCuGxKby5aD9v/LCPG7q/AWhXpju/DWiJf4WiD3/esB1waS9oHSFgYF68MiEeK2mEhBDCHlVqCTonGsdeon8V85D3iXsmciHhQvYhzg5a5rzSEAethi2h1/kmVEPnOcH8HRqNg8sltM6ROGgcGN+mH5qcrlG2/ebZIP++4F7K2q9KiMdOGiEhhLBHDi7mZgh42+hCk1JNSMtKY9j2YaRnpWcf5uvjwYhONQE4dUODwajSukZx2jc9C5iHzBd1ysGZIICLwXDxH9Doofkg674eIWxEGiFxl9at/9/encc1ceZ/AP9MAoQ7gCjBA7lEQRdRbBVBgbqIV2tbS72KsB5VW496a/HCSq3aqlRbV1tX6bq1rVp2W+sPYVEQEZHiWTxQhOIKFhQqiNx5fn+kTA0kkGgghHzfrxcvyMwzM59nQpJv5gzAe++91+rTPKvGy2r8mDGGt99+GzY2NuA4DpcuXZIbJhQKcfXq1TbJSkircgsGAAhv/xcfDf8INsY2uFV6C5szNss1+5uvI9707gYHM4a9bw3AlomOSLt/CgAwpU/Ld5nnNWwNGvAWIO6ukS4Qom0G2g5AtCM8PBwxMTFNht+6dQvff/89DA0NFUylXONpAgIC4OXlhR07djxvVLWXHRcXhwMHDiApKQnOzs6wtbWVG+bo6AgjI6NWz6WL2vJ5IxrQKxjAEuBuOmyZAB8N+wizE2bjSPYRvCh5EaOdRgOQ3bg16tW+OH78VwT27ow9v+xBHavDwC4D4d7JXbVl/e9n4M4pQGAA+C1qvT4R0sZoi5AeGzVqFAoLC+V+nJycYGNjAwsLi5Zn8JRnmUZTGi87JycH9vb2GDp0KCQSCQwMDBQOU1dNTU3LjXRUR+5bh2bVA+jSF2BS4HYifLr6YJbnLADA+rPr8WvZr00mUeUu8wo1bA3ynARY93zu6IS0F1QI6TGRSASJRCL3IxQKFe56WrBgAZYvXw4bGxtIJBJERkbKzevpacLDw5GcnIzo6GhwHAeO45CXlwfGGLZs2QJnZ2eYmJigf//+OHLkSLMZKyoqMG3aNJibm8Pe3h6ffPJJkzaNlz1//nzk5+eD4zg4Ojo2Gebs7AwALeYJCAjAvHnzsHjxYtja2iIoKEil6ZSts/Xr1/PjpVIpNm/eDFdXV4hEIjg4OCAqKoofr+66+vHHH2FlZQWpVHYV4UuXLoHjOCxbtoxvM3v2bEyePFlp35Q9b6o4dOgQjI2Nce/en/e3mjlzJjw9PfHo0SOV5kGekdtI2e/sOADA3P5z4W3njSd1T7A0eSmq66vlmsf/Gt/sXeYVKrgE3DoBcAJg2GINhidE+6gQIiqJiYmBmZkZ0tPTsWXLFnzwwQc4deqUwrbR0dHw8fHBrFmz+C1NPXr0wOrVq7F//37s3r0bWVlZWLRoEd566y0kJycrXe6yZctw6tQpxMbGIj4+HklJScjMzFTaPjo6Ghs2bED37t1RWFiIjIyMJsPS09MBAGvWrGkxT0xMDAwMDJCamoo9e/YAgMr9aLzONmzYgIQE2a0MVq1ahc2bN2PNmjW4du0avv76a9jZ2fHTqruuhg8fjvLycly8eBEAkJycDFtbW7n2SUlJ8Pf3V9o3Zc+bKiZNmoTevXtj0ybZtWwiIyNx4sQJ/N///R/EYroHVatyGyX7ffu/QH0dDAQG2DxsM6xF1rhRcgMfZ3zMN2WM4VD2IQDApD6T5O4y36zTW2W/+70BdHLRZHpCtI6OEdIkxoCnru7aLKlU1rZGCAg0UI8amgKNL4PfgmPHjsHc3Jx/PHr0aBw+fFhhW09PT6xbtw4A0KtXL+zatQvJyckYP358k7ZisRhGRkYwNTWFRCI7vbaiogLbtm3DyZMn4ePjAwBwdnbGmTNnsGfPHrkP6AaPHz/Gvn378NVXX/FbY2JiYtC9u/KDNMViMSwsLCAUCvllA5AbJpVKUVhYiO3bt7eYx9XVFVu2bOHno04/FK2zxMREDBkyBNHR0di1axfCwsIAAC4uLvDz81NpGcOGDVPYby8vLyQlJcHb2xtJSUlYtGgRIiMjUV5ejoqKCmRnZyMgIICfpnHfADR53lTFcRyioqLwxhtvoGvXroiOjkZKSgq6devGt3nttdeQlJSE4cOHIzY2Vq35k2Z0fwEwsQYqS4H/nQd6DoWdmR0+HPYh5v53Lr65+Q1ekLyAwG6BuFt/F9cfXZfdZb7XBNXm/1sWcOMYAA4YvrRVu0KINlAhpEm1T4APu6rUVADASpPLfr8AMDJTa5LAwEDs3r2bf2xmpnx6T09PuccSiQQPHii+bL8i165dQ1VVFV/QNKipqcGAAQMUTpOTk4Oamhq+GABkxwP17t1b5eUqc/PmTZXyDBo0SG68Ov1ovM7s7e1RVFSE69evo7q6GiNGjFCY7VnWFSDb3ZWUlITFixcjJSUFGzduxNGjR3HmzBn8/vvvsLOzQ58+fZT27XmNGzcOHh4eiIyMRHx8PPr27Ss3fsGCBQgPD8c//vEPjS5X7wmEgGsQcPU72e6xnkMBAH7d/DCj3wzs+2Uf1p1dh16jeyGtOg2AmqfMN9xh3mM80Pn5X3uEtDdUCOkxMzMzuLq6qtS28VlkHMfxx6OooqHtTz/9JLeVAJAdq6QIY0zl+atL1TyNi0N1+qFsnZmYmGgkW2MBAQHYt28fLl++DIFAAA8PD/j7+yM5ORmlpaVNtro1V/g+ixMnTuDGjRuor6+X283XIDAwECdPntToMskf3IL/KITigaAN/OB3B7yLzN8ycan4EhafXow7tbKLLap8ynxxNpD1x9a74cuab0uIjqJCSJMMTWVbZlQglUpRVl4OSwsLCDS1a6wdMTIyQn19Pf/Yw8MDIpEI+fn5CneDKeLq6gpDQ0OcO3cODg4OAIDS0lJkZ2erPA9levfurXYe4Nn60VivXr1gYmKCxMREzJw5U+1lKCtAG44T2rFjB/z9/cFxHPz9/bFp0yaUlpZi4cKWL4DX+HlT1YULFxASEoI9e/bgm2++wZo1a5TuZiWtwOUlgBMCxdeB0l/5s7oMBYbY6r8Vb/z4Bm7/LrtD/YDOA1Q/ZT7lEwAM6D0WkPRrpfCEaBcVQprEcarvnpJKAcN6WXtNFELtjKOjI9LT05GXlwdzc3PY2Nhg6dKlWLRoEaRSKfz8/FBWVoazZ8/C3NycP1bmaebm5pgxYwaWLVuGTp06wc7ODhERERopHC0sLLBkyRK18jRMp24/GjM2NsaKFSuwfPlyGBkZwdfXF8XFxcjKysKMGTNaXEZoaKjC+TYcJ3Tw4EFER0cDkBVHISEhqK2tlTs+SBlFz5tAIMCuXbsQGxuLxMTEJtPk5eVh7NixWLlyJUJDQ+Hh4YEXXngBmZmZ8Pb2bnGZRANMbYAeg4H8s8CteODFWfwoiZkEUb5RmHdSdpf4yb0nqzbPkjvA1T+KWX/aGkQ6LiqESKtYunQpwsLC4OHhgcrKSuTm5uKDDz5Aly5dsGnTJty5cwdWVlYYOHAg3n//faXz2bp1Kx4/foxXXnmFL140dTr2hg0bYGdnp1YeAM/Uj8bWrFkDAwMDrF27FgUFBbC3t8ecOXOeexmBgYG4cOECX/RYW1vDw8MDBQUFcHdveSuAoufN0dERDx48QE5OTpP2JSUlGD16NF555RU+m7e3N15++WVEREQgLi5O5XVCnpNbsKwQyo6TK4QAwL+HP9a8uAbJl5MR2D1QtfmlbANYvez4o67Kj00jRNdxrDUPxOgAysrKIBaL8ejRI1haWsqNq6qqQm5uLpycnGBsbKzWfKVSKcrKymBpaamZXWNtTJfz63J2QLfznzx5EtHR0YiNjVWa/XleV62ttrYWx48fx5gxY9S++nqrK7oOfD5Edlf4FblNtk6rlb30V2DnQEBaB8xIAHq82IrBVdOu130LdDk7oLv5m/v8fppuvYsSQnRWcHAwJk6ciISEBDg4OCAjI0PbkTqWzn0AKwegvhq4o/zaXCpJ3SErgpz820URREhrol1jhJA2ceLECZ3emtXucZzs4orn98quAt1nzLPNp6wAuHhQ9rf/Cs3lI6SdonciQgjpKHrJ7kaP7HjZBV6fRWo0UF8D9PQFHH01l42QdooKIUII6Sgc/WSX0igvAO5fVX/68t+AzAOyv+m6QURPUCFECCEdhaEx4Bwg+zv7hPrTp+0E6qpkt+1omA8hHRwVQoQQ0pG4/bF77JaahVDFQyDjj9ufDF+u9r0LCdFVVAgRQkhH0muk7Pf/fgYeF6s+3bnPgNoKwN4L6BXUYnNCOgoqhAghpCOx7ApIPAEw4HaCatNUlgLpe2V/D19GW4OIXqFCiBBCOpqG3WOqHieUvgeoKQe69AV6P+Np94ToKCqECCGko3EbJfudcxKor22+bVUZcO5z2d/Dl3bIex8S0hz6jyeEkI6m60DA1BaoLgPy05pvm/EFUPUIsHUDPMa3TT5C2hEqhAghpKMRCP48aLq53WM1FUDaZ7K/hy0FBMLWz0ZIO0OFECGEdERuKhRCP/8DePIQsHYC+k1om1yEtDNUCJEmAgIC8N5777X6NM+q8bIaP2aM4e2334aNjQ04jsOlS5fkhgmFQly9+gxX3SVEl7i8BAgMgIe3gIc5TcfXVgKpn8r+HrYEENKtJ4l+ov98PRUeHo6YmJgmw2/duoXvv/8ehoaGas2v8TQBAQHw8vLCjh07njeq2suOi4vDgQMHkJSUBGdnZ9ja2soNc3R0hJGRUavn0kVt+byRVmYsBhx8gLwU4FY84D1TfnxmDFBRBIgdgP6TtJORkHaACiE9NmrUKOzfv19uWOfOnSEUqn+cgI2NjaZiPfeyc3JyYG9vj6FDhyoc1nAHdHXV1NR02AKqI/dNr7mNkhVC2XHyhVBdtezmqgAwbBEgVO+LDyEdCe0a02MikQgSiUTuRygUKtz1tGDBAixfvhw2NjaQSCSIjIyUm9fT04SHhyM5ORnR0dHgOA4cxyEvLw+MMWzZsgXOzs4wMTFB//79ceTIkWYzVlRUYNq0aTA3N4e9vT0++eSTJm0aL3v+/PnIz88Hx3FwdHRsMszZ2RkAWswTEBCAefPmYfHixbC1tUVQUJBK0ylbZ+vXr+fHS6VSbN68Ga6urhCJRHBwcEBUVBQ/Xt119eOPP8LKygpSqRQAcOnSJXAch2XL/rxx5uzZszF58mSlfVP2vKni0KFDMDY2xr179/hhM2fOhKenJx49eqTSPEgraLieUF4qUF3+5/CLB2U3ZrXsBnhN1U42QtoJ2iKkQYwxVNZVqtRWKpWisq4SBrUGEGjguh0mBibgWvFqsDExMVi8eDHS09ORlpaG8PBweHl5Yfz4pqfbRkdHIzs7G/369cOGDRsAyLY0rV69Gt9//z12796NXr164fTp03jrrbfQuXNn+Pv7K1zusmXLcOrUKcTGxkIikeD9999HZmYmvLy8FLaPjo6Gi4sL9u7di4yMDAiFQhgZGckNa1hPa9asQWxsbLN5YmJiMHfuXKSmpoIxBgAq90PROvP19UVQUBBWrVqFL774Atu3b4efnx8KCwtx48YNftrmljFs2LAm/R4+fDjKy8tx8eJFeHt7Izk5Gba2tkhOTubbJCUlYdGiRXL5nu6bvb29wudNFZMmTcJHH32ETZs2YdeuXYiMjMSJEydw7tw5iMVileZBWkEnV8DGGSi5Ay43GYBAdl2hMztk430XAgYibSYkROuoENKgyrpKDP56sFaWnT4lHaaGpmpNc+zYMZibm/OPR48ejcOHDyts6+npiXXr1gEAevXqhV27diE5OVlhISQWi2FkZARTU1NIJBIAsi0727Ztw8mTJ+Hj4wMAcHZ2xpkzZ7Bnzx6FhdDjx4+xb98+fPXVV/zWmJiYGHTv3l1pn8RiMSwsLCAUCvllA5AbJpVKUVhYiO3bt7eYx9XVFVu2bOHno04/FK2zxMREDBkyBNHR0di1axfCwsIAAC4uLvDz81NpGYoKIbFYDC8vLyQlJcHb25sveiIjI1FeXo6KigpkZ2cjICCAn6Zx3wA0ed5UxXEcoqKi8MYbb6Br166Ijo5GSkoKunXrBgC4e/cuQkNDUVRUBI7jsHbtWkycOFGtZZBnwHFAr2AgfTcEtxMAQTC4q98Bj/IBsy7AwGnaTkiI1lEhpMcCAwOxe/du/rGZmZnStp6ennKPJRIJHjx4oPKyrl27hqqqKr6gaVBTU4MBAwYonCYnJwc1NTV8MQDIjgfq3bu3ystV5ubNmyrlGTRokNx4dfrReJ3Z29ujqKgI169fR3V1NUaMGKEw27OsK0C2uyspKQmLFy9GSkoKNm7ciKNHj+LMmTP4/fffYWdnhz59+ijt2/MaN24cPDw8EBkZifj4ePTt25cfZ2BggB07dsDT0xM5OTkIDAzEuHHjmv2fIxriJiuEuNsJ4HqNgPDsDtlw3wWAoYlWoxHSHlAhpEEmBiZIn5KuUlupVIry8nJYWFhobNeYuszMzODq6qpS28ZnkXEcxx+PooqGtj/99BO/laCBSKR403zDrqjWoGqexh/U6vRD2TozMWn+uXqWdQXICqF9+/bh8uXLEAgE8PDwgL+/P5KTk1FaWtpkq5umi5ATJ07gxo0bqK+vh52dndw4e3t72NvbQyqVonPnzrCxsUFJSQkVQm2hpy9gZA6uogh9730DrjQXMO0EDJqu7WSEtAtUCGkQx3Eq756SSqWoM6iDqaGpRgqh9sbIyAj19fX8Yw8PD4hEIuTn5ys9HqgxV1dXGBoa4ty5c3BwcAAAlJaWIjs7W+V5KNO7d2+18wDP1o/GevXqBRMTEyQmJmLmzJlNxre0DGUFaMNxQjt27IC/vz84joO/vz82bdqE0tJSLFy4sMVsjZ83VV24cAEhISHYs2cPvvnmG6xZs0bpbtaLFy9CKpWiR48eai+HPAMDI8AlELj+I1yK42XDfN4FjKgIJQSgQoi0EkdHR6SnpyMvLw/m5uawsbHB0qVLsWjRIkilUvj5+aGsrAxnz56Fubk5f6zM08zNzTFjxgwsW7YMnTp1gp2dHSIiIjRSOFpYWGDJkiVq5WmYTt1+NGZsbIwVK1Zg+fLlMDIygq+vL4qLi5GVlYUZM2a0uIzQ0FCF8204TujgwYOIjpadGj18+HCEhISgtrZW7vggZRQ9bwKBALt27UJsbCwSExObTJOXl4exY8di5cqVCA0NhYeHB1544QVkZmbC29tbru3Dhw8xd+5cfPnlly1mIRrUKxi4/iMAgBlbgXthlpYDEdJ+UCFEWsXSpUsRFhYGDw8PVFZWIjc3Fx988AG6dOmCTZs24c6dO7CyssLAgQPx/vvvK53P1q1b8fjxY7zyyit88aKp07E3bNgAOzs7tfIAeKZ+NLZmzRoYGBhg7dq1KCgogL29PebMmfPcywgMDMSFCxf4osfa2hoeHh4oKCiAu7t7i7kUPW+Ojo548OABcnKaXp24pKQEo0ePxiuvvMJn8/b2xssvv4yIiAjExcXxbaurqzFhwgS89957ctd4Im2g4b5jAKQvvA2hsaUWwxDSvnCsNQ/E6ADKysogFovx6NEjWFrKv3lUVVUhNzcXTk5OMDY2Vmu+DRf1s7S01MldY7qcX5ezA7qZnzGGKVOmwM3NDYsWLWo2+/O8rlpbbW0tjh8/jjFjxqh99XVtq/9hIR7dPAOLOSdgaGGr7Thq0+V1r8vZAd3N39zn99N0412UEKLTUlNT8e233+I///kPhg0bhoEDB9L93tqYdPTHSHFbK7v1BiGER7vGCCGtzs/PD1KpVCe3ZhFCOjZ6JyKEEEKI3qJCiBBCCCF6iwohQgghhOgtKoQIIYQQoreoENIAugIBIZpDrydCSFuiQug5NFxP4cmTJ1pOQkjHUVNTAwAQCoVaTkII0Qd0+vxzEAqFsLKyQlFREQDA1NQUHMepNK1UKkVNTQ2qqqp08jRiXc6vy9kB3c7fUnapVIri4mKYmprCwIDengghrY/eaZ6TRCIBAL4YUhVjDJWVlTAxMVG5eGpPdDm/LmcHdDu/KtkFAgEcHBx0rm+EEN1EhdBz4jgO9vb26NKlC2pra1Werra2FqdPn8bw4cN16pLlDXQ5vy5nB3Q7vyrZjYyMdG5LFyFEd1EhpCFCoVCtYxqEQiHq6upgbGyscx9mgG7n1+XsgG7n1+XshJCOib52EUIIIURvUSFECCGEEL1FhRAhhBBC9BYdI9SChou7lZWVaXS+tbW1ePLkCcrKynTyWAldzq/L2QHdzq/L2QHdzq/L2QHdzq/L2QHdzd/wud3SRVqpEGpBeXk5AKBHjx5aTkIIIYQQdZWXl0MsFisdzzG6nn2zpFIpCgoKYGFhodHrmpSVlaFHjx64e/cuLC0tNTbftqLL+XU5O6Db+XU5O6Db+XU5O6Db+XU5O6C7+RljKC8vR9euXZu9JAdtEWqBQCBA9+7dW23+lpaWOvWP1Zgu59fl7IBu59fl7IBu59fl7IBu59fl7IBu5m9uS1ADOliaEEIIIXqLCiFCCCGE6C0qhLREJBJh3bp1EIlE2o7yTHQ5vy5nB3Q7vy5nB3Q7vy5nB3Q7vy5nB3Q/f0voYGlCCCGE6C3aIkQIIYQQvUWFECGEEEL0FhVChBBCCNFbVAgRQgghRG9RIdTG8vLyMGPGDDg5OcHExAQuLi5Yt24dampq5Nrl5+fj5ZdfhpmZGWxtbbFgwYImbbQlKioKQ4cOhampKaysrBS2ycjIwIgRI2BlZQVra2uMHDkSly5datOciqiSHQAOHDgAT09PGBsbQyKRYN68eW0Xshmq5geAhw8fonv37uA4Dr///nub5GtOS9kvX76MyZMno0ePHjAxMYG7uzuio6PbPqgCqqz39vyabSw7Oxvjx4+Hra0tLC0t4evri1OnTmk7llp++uknDB48GCYmJrC1tcXrr7+u7Uhqqa6uhpeXFziOaxfvjapQ9fNL11Ah1MZu3LgBqVSKPXv2ICsrC9u3b8ff//53vP/++3yb+vp6jB07FhUVFThz5gy++eYbHD16FEuWLNFi8j/V1NQgJCQEc+fOVTi+vLwcwcHBcHBwQHp6Os6cOQNLS0sEBwejtra2jdPKayk7AGzbtg0RERFYuXIlsrKykJiYiODg4DZMqZwq+RvMmDEDnp6ebZBKNS1lz8zMROfOnXHw4EFkZWUhIiICq1atwq5du9o4aVMtZW/vr9nGxo4di7q6Opw8eRKZmZnw8vLCuHHjcP/+fW1HU8nRo0cRGhqKv/3tb7h8+TJSU1MxZcoUbcdSy/Lly9G1a1dtx1CLKp9fOokRrduyZQtzcnLiHx8/fpwJBAJ27949ftihQ4eYSCRijx490kZEhfbv38/EYnGT4RkZGQwAy8/P54dduXKFAWC3b99uw4TKKcteUlLCTExM2H//+9+2D6UGZfkbfP7558zf358lJiYyAKy0tLTNsrWkpexPe+edd1hgYGDrBlKDsuy68ppljLHi4mIGgJ0+fZofVlZWxgC0+/97xhirra1l3bp1Y19++aW2ozyz48ePsz59+rCsrCwGgF28eFHbkZ5Z488vXURbhNqBR48ewcbGhn+clpaGfv36yX1bCA4ORnV1NTIzM7URUS29e/eGra0t9u3bh5qaGlRWVmLfvn3o27cvevbsqe14zUpISIBUKsW9e/fg7u6O7t27480338Tdu3e1HU1l165dw4YNG/DVV181e6NBXdD4tdFe6dJrtlOnTnB3d8dXX32FiooK1NXVYc+ePbCzs4O3t7e247XowoULuHfvHgQCAQYMGAB7e3uMHj0aWVlZ2o6mkt9++w2zZs3CP//5T5iammo7znPTlddoc3T7XbIDyMnJwc6dOzFnzhx+2P3792FnZyfXztraGkZGRjqx6drCwgJJSUk4ePAgTExMYG5ujhMnTuD48eMwMGjf9/m9c+cOpFIpPvzwQ+zYsQNHjhxBSUkJgoKCdGI/eHV1NSZPnoytW7fCwcFB23GeS1paGr777jvMnj1b21FapEuvWY7jkJCQgIsXL8LCwgLGxsbYvn074uLiWjzurD24c+cOAGD9+vVYvXo1jh07Bmtra/j7+6OkpETL6ZrHGEN4eDjmzJmDQYMGaTvOc1P0+aWLqBDSkPXr14PjuGZ/fv75Z7lpCgoKMGrUKISEhGDmzJly4ziOa7IMxpjC4drKr0xlZSWmT58OX19fnDt3Dqmpqejbty/GjBmDysrKdp1dKpWitrYWn376KYKDgzFkyBAcOnQIt27darWDSTWZf9WqVXB3d8dbb73VKlkb02T2p2VlZWH8+PFYu3YtgoKCWiG55rO39Wu2MVX7wxjDO++8gy5duiAlJQXnz5/H+PHjMW7cOBQWFrZJ1ufJL5VKAQARERGYMGECvL29sX//fnAch8OHD7fr7Dt37kRZWRlWrVqllZzKaPrzS9e076/nOmTevHmYNGlSs20cHR35vwsKChAYGAgfHx/s3btXrp1EIkF6errcsNLSUtTW1jb51qkp6uZvztdff428vDykpaXxu2a+/vprWFtb4z//+U+Ly1GXJrPb29sDADw8PPhhnTt3hq2tLfLz8585Y3M0mf/kyZO4evUqjhw5AkD2QQwAtra2iIiIQGRk5HNlbUyT2Rtcu3YNL730EmbNmoXVq1c/R7rmaTK7Nl6zjanan5MnT+LYsWMoLS2FpaUlAODzzz9HQkICYmJisHLlyraI24Sq+cvLywHIv0ZFIhGcnZ1b7TXaElWzb9y4EefOnWtyz65BgwZh6tSpiImJac2YSmny80sXUSGkIba2trC1tVWp7b179xAYGMh/k2l8HIePjw+ioqJQWFjIfzDHx8dDJBK12j58dfK35MmTJxAIBHLfhBseN3yb0yRNZvf19QUA3Lx5E927dwcAlJSU4MGDB612fJMm8x89elRuq1tGRgamT5+OlJQUuLi4aGQZT9NkdkC2Jeill15CWFgYoqKiNDZfRTSZXRuv2cZU7c+TJ08AoMn7jkAgaJXXp6pUze/t7Q2RSISbN2/Cz88PAFBbW4u8vDytHYOoavZPP/0UGzdu5B8XFBQgODgY3377LQYPHtyaEZulyc8vXUSFUBsrKChAQEAAHBwc8PHHH6O4uJgfJ5FIAAAjR46Eh4cHQkNDsXXrVpSUlGDp0qWYNWsW/w1Om/Lz81FSUoL8/HzU19fz18BwdXWFubk5goKCsGzZMrz77ruYP38+pFIpPvroIxgYGCAwMLBdZ3dzc8P48eOxcOFC7N27F5aWlli1ahX69Omj9exAy/kbFzsPHjwAALi7u2v9+I+WsmdlZSEwMBAjR47E4sWL+WNrhEIhOnfurMXkLWdv76/Zp/n4+MDa2hphYWFYu3YtTExM8MUXXyA3Nxdjx47VdrwWWVpaYs6cOVi3bh169OiBnj17YuvWrQCAkJAQLadrXuPj9szNzQEALi4u/Bev9kyVzy+dpNVz1vTQ/v37GQCFP0/79ddf2dixY5mJiQmzsbFh8+bNY1VVVVpKLS8sLExh/lOnTvFt4uPjma+vLxOLxcza2pq99NJLLC0tTXuh/6BK9kePHrHp06czKysrZmNjw1577TW5SwFokyr5n3bq1Kl2c/p8S9nXrVuncHzPnj21mpsx1dZ7e37NNpaRkcFGjhzJbGxsmIWFBRsyZAg7fvy4tmOprKamhi1ZsoR16dKFWVhYsL/+9a/sl19+0XYsteXm5urU6fOqfn7pGo6xPw4iIIQQQgjRM7q/c48QQggh5BlRIUQIIYQQvUWFECGEEEL0FhVChBBCCNFbVAgRQgghRG9RIUQIIYQQvUWFECGEEEL0FhVChJB2Lzw8HK+++qq2YxBCOiAqhAjRU0VFRZg9ezYcHBwgEokgkUgQHByMtLQ0vg3Hcfj3v/+tvZB/iI6OxoEDB7Qdo8OgwpKQP9G9xgjRUxMmTEBtbS1iYmLg7OyM3377DYmJiSgpKdF2tCbEYrG2IxBCOipt3+ODENL2SktLGQCWlJSktE3Pnj2V3vPrhx9+YAMHDmQikYg5OTmx9evXs9raWn48APb555+zUaNGMWNjY+bo6Mi+++67ZjMdPnyY9evXjxkbGzMbGxs2YsQI9vjxY8aY7F5f48ePZ4z9eX+mxj/+/v78vFJTU9mwYcOYsbEx6969O5s/fz4/L2Wa61NkZCSzt7dnDx484Nu//PLLbNiwYay+vl7lPl+5coUFBgbyfZw1axYrLy/nxzf0c+vWrUwikTAbGxv2zjvvsJqaGr5NdXU1W7ZsGevatSszNTVlL774otw9z/bv38/EYjGLi4tjffr0YWZmZiw4OJgVFBQwxhTf003ZveoI0QdUCBGih2pra5m5uTl77733lN4YtKioiAFg+/fvZ4WFhayoqIgxxlhcXByztLRkBw4cYDk5OSw+Pp45Ojqy9evX89MCYJ06dWJffPEFu3nzJlu9ejUTCoXs2rVrCpdVUFDADAwM2LZt21hubi67cuUK++yzz/gi4elCqK6ujhUWFvI/Fy9eZJ06dWJr1qxhjMmKDXNzc7Z9+3aWnZ3NUlNT2YABA1h4eLjS9dFSn+rq6piPjw979dVXGWOM7d69m4nFYpaXl6dynysqKljXrl3Z66+/zq5evcoSExOZk5MTCwsL4+cRFhbGLC0t2Zw5c9j169fZjz/+yExNTdnevXv5NlOmTGFDhw5lp0+fZrdv32Zbt25lIpGIZWdnM8ZkhZChoSH761//yjIyMlhmZiZzd3dnU6ZMYYwxVl5ezt588002atQofh1WV1crXTeEdHRUCBGip44cOcKsra2ZsbExGzp0KFu1ahW7fPmyXBsALDY2Vm7YsGHD2Icffig37J///Cezt7eXm27OnDlybQYPHszmzp2rMEtmZiYDIFdYPO3pQuhplZWVbPDgwWzcuHH8lpnQ0FD29ttvy7VLSUlhAoGAVVZWKpy/Kn3KyclhFhYWbMWKFczU1JQdPHhQrn1Lfd67dy+ztraW2zL1008/MYFAwO7fv8/3s2fPnqyuro5vExISwiZOnMgYY+z27duM4zh27949ueWMGDGCrVq1ijH25x3Cb9++zY//7LPPmJ2dHf9Y2fokRB/RMUKE6KkJEyZg7NixSElJQVpaGuLi4rBlyxZ8+eWXCA8PVzpdZmYmMjIyEBUVxQ+rr69HVVUVnjx5AlNTUwCAj4+P3HQ+Pj64dOmSwnn2798fI0aMwF/+8hcEBwdj5MiReOONN2Btbd1sH2bMmIHy8nIkJCRAIBDw+W7fvo1//etffDvGGKRSKXJzc+Hu7v5MfXJ2dsbHH3+M2bNnY+LEiZg6dWqT+TTX5+vXr6N///4wMzPjx/v6+kIqleLmzZuws7MDAPTt2xdCoZBvY29vj6tXrwIALly4AMYY3Nzc5JZTXV2NTp068Y9NTU3h4uIiN4+ioiIla5EQ/UaFECF6zNjYGEFBQQgKCsLatWsxc+ZMrFu3rtlCSCqVIjIyEq+//rrC+TWH4ziFw4VCIRISEnD27FnEx8dj586diIiIQHp6OpycnBROs3HjRsTFxeH8+fOwsLCQyzd79mwsWLCgyTQODg7P1afTp09DKBQiLy8PdXV1MDBo+S20oc+MMaX9f3q4oaFhk3FSqZTPKRQKkZmZKVcsAYC5uXmz82CMtZiVEH1Ep88TQngeHh6oqKjgHxsaGqK+vl6uzcCBA3Hz5k24uro2+WnYKgMA586dk5vu3Llz6NOnj9JlcxwHX19fREZG4uLFizAyMkJsbKzCtkePHsWGDRvw3XffyW35aMiXlZWlMJ+RkZHC+anSp2+//Rbff/89kpKScPfuXXzwwQdN5tNcnz08PHDp0iW59ZuamgqBQNBkC48yAwYMQH19PYqKiprklEgkKs0DAIyMjJo8r4ToK9oiRIgeevjwIUJCQjB9+nR4enrCwsICP//8M7Zs2YLx48fz7RwdHZGYmAhfX1+IRCJYW1tj7dq1GDduHHr06IGQkBAIBAJcuXIFV69excaNG/lpDx8+jEGDBsHPzw//+te/cP78eezbt09hnvT0dCQmJmLkyJHo0qUL0tPTUVxcrHA31i+//IJp06ZhxYoV6Nu3L+7fvw9A9uFuY2ODFStWYMiQIXj33Xcxa9YsmJmZ4fr160hISMDOnTsVLr+lPv3vf//D3LlzsXnzZvj5+eHAgQMYO3YsRo8ejSFDhqjU56lTp2LdunUICwvD+vXrUVxcjPnz5yM0NJTfLdYSNzc3TJ06FdOmTcMnn3yCAQMG4MGDBzh58iT+8pe/YMyYMSrNx9HRESdOnMDNmzfRqVMniMXiJluRCNEb2j1EiRCiDVVVVWzlypVs4MCBTCwWM1NTU9a7d2+2evVq9uTJE77dDz/8wFxdXZmBgYHc6fNxcXFs6NChzMTEhFlaWrIXX3xR7swmAOyzzz5jQUFBTCQSsZ49e7JDhw4pzXPt2jUWHBzMOnfuzEQiEXNzc2M7d+7kxz99cG/DwcCNf54+ff78+fMsKCiImZubMzMzM+bp6cmioqKaXSfK+iSVStmIESNYcHAwk0qlfPtFixYxFxcX/sw2Vfqs6unzT1u4cKFc32pqatjatWuZo6MjMzQ0ZBKJhL322mvsypUr/PoRi8Vy84iNjWVPv90XFRXx6wd0+jzRcxxjtOOYEKJZHMchNjZWr65erI99JqQjoGOECCGEEKK3qBAihBBCiN6iXWOEEEII0Vu0RYgQQggheosKIUIIIYToLSqECCGEEKK3qBAihBBCiN6iQogQQggheosKIUIIIYToLSqECCGEEKK3qBAihBBCiN6iQogQQggheuv/AVLPbYy0q9cZAAAAAElFTkSuQmCC\n",
                        "text/plain": [
                            "<Figure size 640x480 with 1 Axes>"
                        ]
                    },
                    "metadata": {},
                    "output_type": "display_data"
                }
            ],
            "source": [
                "h_lst = 10.**(-np.arange(1,21)) # step sizes [1e-1, ..., 1e-20]\n",
                "\n",
                "for i in range(3):\n",
                "    # Plot error compared to analytical gradient, df(x)\n",
                "    plt.semilogy(np.log10(h_lst), [np.abs(df(x)[i] - (f(x+np.roll([h,0,0],i))-f(x))/h) for h in h_lst], \n",
                "                 label=f'Finite difference wrt. $x_{i}$')\n",
                "plt.xticks(np.arange(-20,-1,2))\n",
                "setup_plot(ylabel='Error of gradient', xlabel='Step size exponent')"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "0efc0482",
            "metadata": {},
            "source": [
                "### Complex step\n",
                "\n",
                "The complex step method is described [here](https://blogs.mathworks.com/cleve/2013/10/14/complex-step-differentiation/).\n",
                "\n",
                "It utilizes that \n",
                "\n",
                "$\\frac {d f(x)}{x}= \\frac{\\operatorname{Im}(f(x+ih))}{h}+O(h^2)$\n",
                "\n",
                "Applied to the example function, the result is accurate to the 15th decimal."
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 6,
            "id": "c14cab89",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "Analytical gradient: [6.129430520583658, 15.164788859062082, -45.83911438119122]\n",
                        "Finite difference gradient wrt. x0: 6.129430520583658\n",
                        "Finite difference gradient wrt. x1: 15.164788859062082\n",
                        "Finite difference gradient wrt. x2: -45.83911438119122\n"
                    ]
                }
            ],
            "source": [
                "print (\"Analytical gradient:\", list(df(x)))\n",
                "h = 1e-10\n",
                "\n",
                "for i in range(3):\n",
                "    print (f\"Finite difference gradient wrt. x{i}:\", np.imag(f(x+np.roll([h*1j,0,0],i)))/h)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "b6f26658",
            "metadata": {},
            "source": [
                "Furthermore, the result is much less sensitive to the step size as seen below"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 7,
            "id": "ebebf371",
            "metadata": {},
            "outputs": [
                {
                    "data": {
                        "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlMAAAGwCAYAAACNeeBZAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAA9hAAAPYQGoP6dpAAB5TUlEQVR4nO3deVwU9R/H8dey3DeIoCgg3iCeaIo3KeKRV1qW5ZFlqZWa9avs8Cq106w8yiyPyvJKKzWVvPA+UPI+8AgPFAEFBDl3fn+QWwgqxy6zLJ/n48HjsTs7zL4/u8B+mPnOdzSKoigIIYQQQogSsVA7gBBCCCFEeSbNlBBCCCFEKUgzJYQQQghRCtJMCSGEEEKUgjRTQgghhBClIM2UEEIIIUQpSDMlhBBCCFEKlmoHKK90Oh1XrlzByckJjUajdhwhhBBCFIGiKKSmpuLt7Y2FhWH2KUkzVUJXrlzBx8dH7RhCCCGEKIGLFy9SvXp1g2xLmqkScnJyAvLeDGdnZ4NtNzs7m40bN9KlSxesrKwMtl01SU2mz9zqAfOrydzqAampPDC3egCSkpLw9/fXf44bgjRTJXTn0J6zs7PBmyl7e3ucnZ3N5gdXajJ95lYPmF9N5lYPSE3lgbnVA3k1AQYdoiMD0IUQQgghSkGaKSGEEEKIUpBmSgghhBCiFGTMlBBCCKPIzc3Vj08pTHZ2NpaWlmRkZJCbm1uGyYzH3Goqj/VYWVmh1WrL9DmlmRJCCGFQiqJw9epVbt68+cD1qlSpwsWLF81mvj5zq6m81uPq6kqVKlXKLLM0U0IIIQzqTiPl6emJvb39PT/QdDodt27dwtHR0WCTJ6rN3Goqb/UoikJ6ejrx8fEAVK1atUyeV5opIYQQBpObm6tvpCpVqnTfdXU6HVlZWdja2paLD+qiMLeaymM9dnZ2AMTHx+Pp6Vkmh/zKxysjhBCiXLgzRsre3l7lJKIiu/Pzd78xe4YkzZQQQgiDK0/ja4T5KeufP2mmhBBCCCFKQZopIYQQQohSkGZKCCGEuI+OHTsyduzYIq8fGxuLVqslOjraaJn+q0aNGsycOVN/X6PRsHr1av39kydP0qpVK2xtbWnSpMk9l4mSk7P5TEzirUySMuHyzdtYWpbNwDljy8nJMbua0OWiKGqHEEIYytChQ1m0aFGB5WfOnOGXX34p1kV+q1WrxuXLl/H09ARg69athIaGcuPGDVxdXQ0V+Z7i4uJwc3PT3584cSIODg6cOnUKR0fHey4TJSfNlIl5+9fjbDppyeSD29WOYmDmV1MdZwuCQtKp7eWidhQhhAF07dqVBQsW5FtWuXLlYp9ar9VqqVKlimpTCVSpUiXf/bNnz9KjRw/8/Pzuu6y4srKysLa2LvH3mxM5zGdirLQWWGkUbCwtzOrL3GrSaOBMigWPzNrF19vOkpOrU/tHRwiTpSgK6Vk5hX7dzsq952Ol/VKKufvYxsaGKlWq5PvSarUFDvPVqFGDadOmMWzYMJycnPD19WXevHn6x/97mO/ChQuEhoYC4ObmhkajYejQofrX5aOPPqJmzZrY2dnRuHFjVqxYcd+M8fHx9OzZEzs7O/z9/fnxxx8LrPPfw3wajYaoqCimTJmCRqNh0qRJhS4DuHz5MgMGDMDNzY1KlSrRu3dvLly4oN/u0KFD6dOnD9OnT8fb25u6desW6/s++eQTqlatSqVKlXjxxRfzTVuQmZnJ66+/jo+PDzY2NtSpU4dvv/1W//jx48fp3r07jo6OeHl5MWjQIBISEu77WpUl2TNlYr58ojHr1l2me/fwYu1WNmXZ2dmsW7fOrGqKuZbMyG8jOZMC0/84yZrDcXzQryENvGUvlRB3u52dS+CEDWX+vMenhGNvbZyPuU8//ZT33nuPt956ixUrVjBy5Ejat2+vbzDu8PHxYeXKlfTr149Tp07h7Oysn1TynXfe4ZdffmHu3LnUqVOHyMhInn76aSpXrkyHDh0Kfd6hQ4dy8eJFNm/ejLW1NaNHj9bP9l2YuLg4OnfuTNeuXXnttddwdHRkxIgRBZalp6cTGhpKu3btiIyMxNLSkvfff5/u3bsTGRmp396mTZtwdnYmIiJCP9t4Yd/XtWtXDh8+rN9ztWXLFqpWrcqWLVuIiYlhwIABNGnShOHDhwMwePBgdu/ezRdffEHjxo05f/68vlmKi4ujQ4cODB8+nBkzZnD79m3eeOMNHn/8cTZv3lzyN9GApJkSogT83O15MVBHepWGfLD+FEcuJ9Nr1k6eb1+TMZ3qYGtVthfZFEKU3po1a/KNH+rWrRvLly8vdN3u3bszatQoAN544w0+++wztm7dWqCZ0mq1uLu7A+Dp6akfM5WWlsaMGTPYvHkzISEhANSsWZMdO3bw9ddfF9pMnT59mj/++IM9e/bQsmVLAL799lsCAgLuWVOVKlWwtLTE0dFRf/jP0dGxwLLvvvsOCwsL5s+fr5+jacGCBbi6urJjxw769OkDgIODA/Pnz9c3Sff7vq1bt9KlSxcgb6/crFmz0Gq11K9fnx49erBp0yaGDx/O6dOnWbZsGREREXTu3Fn/Wtwxd+5cmjVrxrRp0/TLvvvuO3x8fDh9+nSB11wN0kwJUUIaDTwWXI3OgVWY+Nsx/jh6lblbz7L+6FWmP9qQVjXvfykNISoKOystx6eEF1iu0+lITUnFydnJKOOL7Ir5T01oaChz587V33dwcLjnuo0aNdLf1mg0VKlS5b57iO52/PhxMjIyCAsLy7c8KyuLpk2bFvo9J06cwNLSkubNm+uX1a9f3yCD2qOiooiJicHJySnf8oyMDM6fP6+/37Bhw3zjpO73fWfPntXfb9CgQb6xZ1WrVuXIkSMAREdHo9Vq77k3Lioqii1bthQ6UP7s2bPSTAlhDjydbZn7dDDrj15lwq9HOZ+QxhPz9vDkQ76M714fZ1vzOLQpRElpNJpCD7fpdDpyrLXYW1uaxHXfHBwcqF27dpHWvXvIgkajQacr+tjJO+uuXbuWatWq5XvMxsam0O+5MwbMGLN763Q6goODC4zB0ul0+fLc3WDe6/sgb/D+Hfd7ve4c9rxftp49e/Lhhx8WeKysLmT8INJMCWEgXYOqEFKrEh/8cYKf9l3kp32xbD55jfd6B9GlQZUHb0AIYZbu7MnJzc3VLwsMDMTGxobY2Nh77pG5W0BAADk5ORw4cICHHnoIgFOnTnHz5s1SZ2zWrBlLly7F09MTZ2dn/XKdTkdKSkqxv684GjZsiE6nY9u2bfrDfHc/x8qVK6lRowaWlqbZtqj/r4AQZsTFzorpjzbip+GtqFHJnmspmTz/fRQv/niQ66mZascTQqjAz88PjUbDmjVruH79Ordu3cLJyYnXXnuNV155hUWLFnH27FkOHTrE7NmzC53vCqBevXp07dqV4cOHs3fvXqKionjuueceuGenKJ566ik8PDzo3bs327dv5/z582zbto2xY8dy+fLlYn/fmDFjuHTpUpGeu0aNGgwZMoRhw4axevVqzp8/z9atW1m2bBkAL774IklJSTz55JPs27ePc+fOsXHjRoYNG5avQVWTNFNCGEFIrUqsH9ueER1qobXQsPZIHJ1nbGPZgYvFPl1bCFG+VatWjcmTJ/Pmm2/i5eXFSy+9BMB7773HhAkTmD59OgEBAYSHh/P777/j7+9/z20tWLAAHx8fOnTowKOPPsrzzz+vnxy0NOzt7YmMjMTX15dHH32UgIAAhg0bxu3btwuMhyrq9xVnT9XcuXPp378/o0aNon79+gwfPpy0tDQAvL292blzJ7m5uYSHhxMUFMSYMWNwcXExicPDABpF/rKXSEpKCi4uLiQnJ5d412Zh/p1GoLvZTCNQ0Ws6ejmZN385zNHLebvK29b2YFrfhvhWsi+LqEVS0d+j8qC81HNnwLK/vz+2trb3XffOISRnZ2eT+VAsLXOrqbzWc7+fw8TERDw8PAz6+V1+Xhkhyqmgai6sHtWGN7vVx8bSgh0xCXSZuY1vIs/JZJ9CCGEGpJkSogxYai0Y0aEWG8a2J6RmJTKydUxdd4JH5+7iRNy9B3cKIYQwfRW6mVqzZg316tWjTp06zJ8/X+04ogKo4eHAkuEt+eDRhjjZWnL4UjI9v9zBxxtOkpFtGgMphRBCFE+FbaZycnIYN24cmzdv5uDBg3z44YckJSWpHUtUABqNhice8mXTuA50bVCFHJ3C7C1n6f7Fdvadl59BIYQobypsM7Vv3z4aNGhAtWrVcHJyonv37mzYUPbXjhIVl6ezLV8NCuarp5tR2cmGc9fTePzr3by96gipGdkP3oAQQgiTUG6bqcjISHr27Im3t3e+K2T/15w5c/Qj+YODg9m+fbv+sStXruSbdbZ69er3nUtDCGPpGlSVP8d14IkWPgD8uDeWsBmR/Hn8msrJhBBCFEW5babS0tJo3Lgxs2bNKvTxpUuXMnbsWN5++20OHTpEu3bt6NatG7GxsQCFzvVjjCn6hSgKFzsrPujXiCXDW+JXyZ6rKRk8t/gALy6RyT6FEMLUmea87EXQrVs3unXrds/HZ8yYwbPPPstzzz0HwMyZM9mwYQNz585l+vTpVKtWLd+eqEuXLumvwl2YzMxMMjP//VC7M71+dnY22dmGOyRzZ1uG3KbapKaia+Hrwu+jQvhyy1m+2/U3aw/HsfnENfo3q8bQ1n74uhtnbip5j0xfeaknOzsbRVHQ6XQPvFbdnX9q76xvDsytpvJaj06nQ1EUsrOz811gGYzzO2QWk3ZqNBpWrVpFnz59gLyrbtvb27N8+XL69u2rX2/MmDFER0ezbds2cnJyCAgIYOvWrTg7O9OsWTP27NlDpUqVCn2OSZMmMXny5ALLlyxZgr296Uy+KMzHxVuw7JyW2LS8PaYaFBpXUnjYW4dfwYunC2ESLC0tqVKlCj4+Pvpr0onSi42NpXHjxkRGRtKwYUO145i8rKwsLl68yNWrV8nJycn3WHp6OgMHDjTopJ3lds/U/SQkJJCbm4uXl1e+5V5eXly9ehXI+4X/9NNPCQ0NRafT8frrr9+zkQIYP34848aN099PSUnBx8eHLl26GHwG9IiICMLCwkx6luPikJpK7nlFYfe5JL7deYHIM4lEJ2qITrSgRQ03nmtbg451PLCwKP3haXmPTF95qScjI4OLFy/i6Oj4wBnQFUUhNTUVJycnkxhmcfXqVaZNm8a6deu4fPkynp6eNG7cmDFjxtCpU6cibcNYNTk65v0H5eDgYNDPnAe5U09UVBSdO3cmMTERV1fXMnv+ksrIyMDOzo727dsXOgO6oZllM3XH3T/IiqLkW9arVy969epVpG3Z2NhgY2NTYLmVlZVR/rAZa7tqkppKpkP9KnSoX4WTV1OYF3mO36KvsP/CDfZfuEFtT0eeb1eT3k29sbHUPnhjDyDvkekz9Xpyc3PRaDRYWFg88PIjdw4b3VlfTRcuXKBNmza4urry0Ucf0ahRI7Kzs9mwYQMvv/wyJ0+eLNJ2jFXTnW0V5XU1pP/Wo8bzl5SFhQUajabQ3xdj/P6Y/itSAh4eHmi1Wv1eqDvi4+ML7K0SoryoX8WZGY83YfsbobzQviZONpbExN/i9ZWHafvhFmZviSE53bTH0whhqkaNGoVGo2Hfvn3079+funXr0qBBA8aNG8eePXv068XGxtK7d28cHR1xdnbm8ccf59q1f8+8nTx5Mu3ateO7777D19cXR0dHRo4cSW5uLh999BFVqlTB09OTqVOn5nt+jUbD3Llz6datG3Z2dvj7+7N8+fL7Zj5+/Djdu3fH0dERLy8vBg0aREJCAgBbt27F2to631nsn376KR4eHsTFxRW6vb///puePXvi5uaGg4MDDRo0YN26dcTGxur3zLm5uaHRaBg6dCiQt5Pio48+ombNmtjZ2dG4cWNWrFih3+bWrVvRaDSsXbuWxo0bY2trS8uWLTly5EgR3pXywyybKWtra4KDg4mIiMi3PCIigtatW6uUSgjDqOpix/juAewc/zBvda9PFWdbrqdm8vGGU4R8sIkpvx/n0o10tWMK8S9Fgay0wr+y0+/9WGm/ijgkOCkpifXr1/Piiy/i4OBQ4PE7h7UURaFPnz4kJSWxbds2IiIiOHv2LAMGDMi3/oULF1i/fj3r16/np59+4rvvvqNHjx5cunSJbdu28eGHH/LOO+/ka9IA3n33Xfr168dff/3F008/zZNPPsmJEycKzRwXF0eHDh1o0qQJBw4cYP369Vy7do3HH38cgI4dOzJ27FgGDRpEcnIyf/31F2+//TbffPMNVatWLXSbL774IpmZmURGRnLkyBE+/PBDHB0dqVatmr6xO3XqFHFxcXz++ecAvPPOOyxYsIC5c+dy7NgxXnnlFZ5++mm2bduWb9v/+9//+OSTT9i/fz+enp706tXL5E+mKI5ye5jv1q1bxMTE6O+fP3+e6Oho3N3d8fX1Zdy4cQwaNIjmzZsTEhLCvHnziI2NZcSIESqmFsJwnG2teL59LYa29mfN4SvMizzHyaupfLfzPIt2X6BHw6o8374mQdVc1I4qKrrsdJjmXWCxBeBqzOd96wpYF2yO7hYTE4OiKNSvX/++6/35558cPnyY8+fP4+OTNy/c999/T4MGDdi/fz8tWrQA8g6Nffvtt7i4uBAYGEhoaCinTp1i3bp1WFhYUK9ePT788EO2bt1Kq1at9Nt/7LHH9Gegv/fee0RERPDll18yZ86cAlnmzp1Ls2bNmDZtmn7Zd999h4+PD6dPn6Zu3bq8//77/Pnnnzz//PMcO3aMQYMG5Tsp626xsbH069dPP8C9Zs2a6HQ6UlJScHd3B8DT01PfXKalpTFjxgw2b95MSEiI/nt27NjB119/TYcOHfTbnjhxImFhYQAsWrSI6tWrs2rVKn3zV96V22bqwIEDhIaG6u/fGRw+ZMgQFi5cyIABA0hMTGTKlCnExcURFBTEunXr8PPzUyuyEEZhbWnBo82q07dpNbafSWBe5Dl2xCTw219X+O2vK7SpXYnh7WrSoW5lkxjkK4SpuXNS+4N+P06cOIGPj4++kQIIDAzE1dWVEydO6JspX19fnJyc9Ot4eXmh1WrzjTXy8vIiPj4+3/bvNCT/vR8dHV1olqioKLZs2aIfmP5fZ8+epW7dulhbW/PDDz/QqFEj/Pz8mDlz5n3rGz16NCNHjmTjxo107tyZfv36ERQUdM/1jx8/TkZGhr5JuiMrK4umTZveszZ3d3fq1at3z71u5VG5baY6duxY6MSb/zVq1ChGjRpVRomEUJdGo6F93cq0r1uZo5eT+Wb7OdYcjmNnTCI7YxKpX8WJ4e1q0rOxN9aWZnmEX5gqK/u8vUR30el0pKSm4uzkZJxBzVZFm7amTp06aDQaTpw4oZ9ipzB3n8R0r+WWlvk/Wu8MhL57WVHmbbpXg6fT6ejZsycffvhhgcf+exhv165dQN6hzKSkpEIPY97x3HPPER4eztq1a9m4cSPTp0/nk08+YfDgwffMALB27dp8VxQBCj1h627m9M+d/EUVwgwFVXPh8yeaEvl6KM+29cfBWsvJq6m8uvwv2n+0ha+3nSVFrv8nyopGk3e4rbAvK/t7P1baryJ+WLu7uxMeHs7s2bNJS0sr8PjNmzeBvL1QsbGxXLx4Uf/Y8ePHSU5OJiAgoNQv091jqPbs2XPPQ4/NmjXj2LFj1KhRg9q1a+f7utMwnT17lldeeYVvvvmGVq1aMXjw4Ac2cD4+PowYMYJffvmFV199lfnz5wPo5wzLzc3VrxsYGIiNjQ2xsbEFMvx3793dtd24cYPTp08/8LBqeSLNlBBmrJqrHe8+Esiu8Z14o2t9PJ1suJqSwfQ/TtJ6+mamrj1OXPJttWMKobo5c+aQm5vLQw89xMqVKzlz5gwnTpzgiy++0B+i6ty5M40aNeKpp57i4MGD7Nu3j8GDB9OhQweaN29e6gzLly/nu+++4/Tp00ycOJF9+/bx0ksvFbruiy++SFJSEk8++ST79u3j3LlzbNy4kWHDhpGbm0tubi6DBg2iS5cuPPPMMyxYsICjR4/y6aef3vP5x44dy4YNGzh//jwHDx5k8+bN+obHz88PjUbDmjVruH79Ordu3cLJyYnXXnuNV155hUWLFnH27FkOHTrE7NmzWbRoUb5tT5kyhU2bNnH06FGGDh2Kh4fHffcCljfSTAlRAbjYWTGyYy22vxHKR/0bUcfTkVuZOXyz/TztPtzC/1Yc4UrBf8iFqDD8/f05ePAgoaGhvPrqqwQFBREWFsamTZuYO3cukHdYavXq1bi5udG+fXs6d+5MzZo1Wbp0qUEyTJ48mZ9//plGjRqxaNEifvzxRwIDAwtd19vbm507d5Kbm0t4eDhBQUGMGTMGFxcXLCwsmDp1KhcuXGDevHkAVKlShfnz5/POO+/ccxxWbm4uL774IgEBAXTt2pV69eoxe/ZsAKpVq8bkyZN588038fLy0jd57733HhMmTGD69OkEBAQQHh7O77//jr+/f75tf/DBB4wZM4bg4GDi4uL47bffzGqGfLO4nIwaUlJScHFxMeh09JA3y/G6devo3r27SU/MVxxSk+nR6RS2nb7O15Fn2XMuCci7XM3kXoEMbl1T5XSGUd7fo7uVl3oyMjI4f/48/v7+D5wB/c6ZYs7OzuViIsiiKGlNd18WzVSU9j3aunUroaGh3Lhxo0xnTr/fz2FiYiIeHh5yORkhROlYWGgIre9JaH1PDl+6yRd/nubPk9eZ8NsJbmXpGNmhllkNDhVCCGMyj38FhBAl1qi6K3MGNqFLtbyBqR+tP8X0P04+8GxZIYQQeWTPlBACjUZDD18dwQ3rM339aeZFnuNmehbT+jbEUiv/cwlhbOb6z0tRpjEyB/JXUgihN6xNDT7q3wgLDSw7cImXlhwiMyf3wd8ohBAVmDRTQoh8Hm/uw5yngrHWWrD+2FWGLdzPrcwctWOJcqYi7I0Qpqusf/6kmRJCFNA1qAoLnmmBg7WWnTGJPDV/LzfSstSOJcqBO2capqfLxbaFeu78/JXVma8yZkoIUag2tT1YMrwVQxfs46+LN3n86918/2xLqrjc/3R3UbFptVpcXV31152zt7e/7yVRsrKyyMjIMKupEcyppvJWj6IopKenEx8fj6urK1qttkyeV5opIcQ9NfZxZdkLIQz6dh9n4m/R/6td/PBsS2p43Pv6XkJUqVIFoMCFfO+mKAq3b9/Gzs7ObKbiMLeayms9rq6u+p/DsiDNlBDivup4ObF8RAiDvt3LhcR0+n+1m8XDHiLQ23CT1QrzotFoqFq1Kp6enmRn3/sakNnZ2URGRtK+fXuTnoi0OMytpvJYj5WVVZntkbpDmikhxAP5uNuzfERrhny3j+NxKQyYt5sFQ1vQvIa72tGECdNqtff9UNNqteTk5GBra1tuPqgfxNxqMrd6jMX0D4AKIUxCZScbfnq+FS1quJGakcPT3+5ly6n7H8YRQoiKQJopIUSRudhZsXhYS0LrVSYjW8fwRQf4Nfqy2rGEEEJV0kwJIYrFzlrLvMHN6d3Emxydwtil0Xy/52+1YwkhhGqkmRJCFJuV1oLPHm/C4BA/FAXeXX2UWZvPyESNQogKSZopIUSJWFhomNyrAaMfrg3AJxtP8/7aE+h00lAJISoWaaaEECWm0WgY16Ue7z4SCMC3O87z+srD5OTqVE4mhBBlR5opIUSpPdvWn08fa4zWQsOKqEuM+vEgGdlygWQhRMUgzZQQwiD6BVfnq6eDsba0YOPxazyzQC6QLISoGKSZEkIYTFigF4ueeQhHG0t2n0tk4Dd7SJILJAshzJw0U0IIgwqpVYmfhrfC3cGaw5eSeeyrXVy5eVvtWEIIYTTSTAkhDK5hdReWvRBCVRdbzl5P47GvdnPu+i21YwkhhFFIMyWEMIrano6sGNmamh4OXL55m8e+2s3Ry8lqxxJCCIOTZkoIYTTVXO1YNiKEBt7OJKZl8eS8Pew9l6h2LCGEMChppoQQRuXhmHeB5If83UnNzGHwd/vken5CCLMizZQQwuicba1YPOwhOtX3JDNHx5ifoxn90yGS07PVjiaEEKVWYZupixcv0rFjRwIDA2nUqBHLly9XO5IQZs3WSsvXg4IZ27kOWgsNv/11ha6fR7IrJkHtaEIIUSoVtpmytLRk5syZHD9+nD///JNXXnmFtLQ0tWMJYdYstRaM7VyXFSNC8PdwIC45g4Hz9/LemuMyY7oQotyqsM1U1apVadKkCQCenp64u7uTlJSkbighKoimvm6sHd2WgS19gbxr+vWatYPjV1JUTiaEEMVnss1UZGQkPXv2xNvbG41Gw+rVqwusM2fOHPz9/bG1tSU4OJjt27eX6LkOHDiATqfDx8enlKmFEEVlb23JtL4N+W5oczwcrTl97Ra9Z+/gq21nydUpascTQogis1Q7wL2kpaXRuHFjnnnmGfr161fg8aVLlzJ27FjmzJlDmzZt+Prrr+nWrRvHjx/H1zfvv93g4GAyMzMLfO/GjRvx9vYGIDExkcGDBzN//vz75snMzMy3rZSUvP+gs7Ozyc423CDaO9sy5DbVJjWZPjXraVfLnTUvtead1cf48+R1PvjjJJtOXOPjfkFUc7Ur8XblPTJ9UpPpM7d6wDi1aBRFMfl/ATUaDatWraJPnz76ZS1btqRZs2bMnTtXvywgIIA+ffowffr0Im03MzOTsLAwhg8fzqBBg+677qRJk5g8eXKB5UuWLMHe3r5ohQgh7klRYE+8hl8uWJCl02CrVejvr6O5h4JGo3Y6IYS5SE9PZ+DAgSQnJ+Ps7GyQbZbLZiorKwt7e3uWL19O37599euNGTOG6Ohotm3b9sBtKorCwIEDqVevHpMmTXrg+oXtmfLx8SEhIcFgbwbkdcwRERGEhYVhZWVlsO2qSWoyfaZUz99J6fxvxREOXcybLb1bAy8m9wrAzd66WNsxpZoMwdzqAampPCirehRF4af9l+gc4Imnk43RngfyjkhVrVrVoM2UyR7mu5+EhARyc3Px8vLKt9zLy4urV68WaRs7d+5k6dKlNGrUSD8e6/vvv6dhw4aFrm9jY4ONTcE32MrKyig/YMbarpqkJtNnCvXU9nJh+YjWfLXtLDP/PMMfx64RFXuTTx5rTPu6lYu9PVOoyZDMrR6QmsoDY9aTkZ3LW6uO8Muhy/z6VxxLXwjBSmu8Id3GqKNcNlN3aO7a968oSoFl99K2bVt0Op0xYgkhSslSa8FLD9ehfd3KjF0azbnraQz+bh9DW9fgzW71sbXSqh1RCGEAV27eZsQPURy+lIzWQsMjjbyxtCh/x/VN9my++/Hw8ECr1RbYCxUfH19gb5UQovxqVN2VtS+3Y3CIHwALd12gxxfb5YLJQpiBfeeT6DVrB4cvJeNmb8X3wx5iWFv/Iu8UMSXlspmytrYmODiYiIiIfMsjIiJo3bq1SqmEEMZgZ61lSu8gFj7TgspONpy9nkaf2TuZvSVGplAQohxSFIUf9vzNwG/2kHAri4Cqzvz2Ulta1/ZQO1qJmexhvlu3bhETE6O/f/78eaKjo3F3d8fX15dx48YxaNAgmjdvTkhICPPmzSM2NpYRI0aomFoIYSwd63myYWx73vrlCOuPXeXjDafYcjKeGY83wbeSnFErRHmQmZPLpN+O8dO+iwA80qgqH/VvhL21ybYjRWKy6Q8cOEBoaKj+/rhx4wAYMmQICxcuZMCAASQmJjJlyhTi4uIICgpi3bp1+Pn5qRVZCGFk7g7WzH26GSsPXmbSb8c48PcNun0eycSeDXisefVyeXhAiIoiPiWDkT8eJOrvG2g08Hp4fUZ0qGkWv7cm20x17NiRB83aMGrUKEaNGlVGiYQQpkCj0dA/uDot/d0Ztyya/Rdu8PrKw/x54hrTH21IJUfjnlYthCi+Q7E3GPFDFNdSMnG2teSLJ5vSsZ6n2rEMplyOmRJCCB93e35+PoQ3utbHSqth4/FrhM/czpaT8WpHE0L8x7IDFxnw9R6upWRSx9ORX19qa1aNFEgzJYQox7QWGkZ2rMWqUW2o4+lIwq1Mnlm4n7dXHSE9K0fteEJUaNm5Oib9dozXVxwmK1dHl0AvVr3YBn8PB7WjGZw0U0KIci+omgu/v9yWYW38Afhxbyx95uzhQqrKwYSooBJvZfL0/L0s3HUBgLGd6/DV08E42pjs6KJSMc+qhBAVjq2Vlgk9A3m4vievLf+L84npzEzUkuh4kte7BZjtH3EhTM3Ry8m88H0Ul2/exsFay2cDmtClQRW1YxmV7JkSQpiVtnU8WD+2Hb0aVUVBw+I9sYTN2EbE8WtqRxPC7P0afZn+X+3i8s3b+Hs4sPrFNmbfSIE0U0IIM+Rqb82njzVkREAu1d3siEvOYPjiA4z8IYprKRlqxxPC7OTqFKavO8GYn6PJyNbRsV5lVr/YhjpeTmpHKxPSTAkhzFaAq8K6l1rzQoeaaC00/HH0Kp0/3cb3e/5GJ7OnC2EQN9OzGLpgH19HngNgVMdafDukBS525nOh5weRZkoIYdbsrLWM7xbA7y+1pbGPK6mZOby7+ij9v9rFqasyQl2I0jh1NZXes3ey/UwCdlZaZg1syutd66MthxcrLg1ppoQQFUKgtzO/jGzNpJ6BOFhrORh7kx5fbOfjDSfJyM5VO54Q5c76o3H0nbOTvxPTqe5mx8qRrXmkkbfasVQhzZQQosLQWmgY2safiHEdCAv0IkenMHvLWbrOjGRnTILa8YQoF3Q6hRkbTzHih4OkZ+XSulYlfn+pLYHezmpHU400U0KICsfb1Y5vBjfnq6eD8XK24UJiOk/N38u4ZdEkpWWpHU8Ik5WSkc3wxQf4YnMMAM+29WfxsIdwc7BWOZm6pJkSQlRYXYOqEDGuA4ND/NBo4JeDl+n06VZWRl164LVBhahozl6/RZ/ZO9l0Mh5rSws+fawx7z4SiKVWWgl5BYQQFZqzrRVTegexcmRr6nk5cSM9m1eX/8XT3+7lQkKa2vGEMAlbTl2nz6ydnLueRlUXW1aMCKFfcHW1Y5kMaaaEEAJo5uvGmtFteb1rPWwsLdgZk0j4zEhmb4khK0endjwhVKEoChsvaXjhx0OkZubQooYbv73UlkbVXdWOZlKkmRJCiH9YaS0Y1bE2G19pT9vaHmTm6Ph4wyl6frmDqL9vqB1PiDKVlpnD6KWHWXtRi6LA0618+fG5VlR2slE7msmRZkoIIe7iV8mB7599iM8GNMbdwZpT11Lp/9Uu3ll9hJSMbLXjCWF0sYnp9Ju7i/XHrqHVKLzXK5D3+zTE2lLahsLIqyKEEIXQaDT0bVqdP8d1oH9wdRQFftgTS+dPt/HHkTgZoC7M1vYz1+k5awcnr6ZS2dGalxvk8kQLGR91P9JMCSHEfbg7WPPJY41Z8lxLalSyJz41k5E/HmT44gNcuXlb7XhCGIyiKHwTeY4h3+0j+XY2jX1c+WVkK/wrxuX1SkWaKSGEKILWtT1YP7Y9L4XWxtJCw58n4uk8Yxvf7ThPrlznT5RzGdm5vLI0mqnrTqBT4LHg6ix9vhVVnG3VjlYuSDMlhBBFZGul5bXweqwb045gPzfSs3KZsuY4/b/aRaqMpRLl1OWbt+n/1S5WR19Ba6Fhcq8GfNS/EbZWWrWjlRvSTAkhRDHV9XJi+QshvN8nCCcbSw7F3uSTDafUjiVEse09l0ivL3dw9HIK7g7W/PBsS4a0roFGU7EuVFxa0kwJIUQJWFhoeLqVH18NCgZg8Z6/ZfoEUW4oisLi3Rd4av5eEtOyaODtzG8vtSGkViW1o5VL0kwJIUQptKntQb9meWf7vfXLEZngU5i8zJxc3lx5hAm/HiNHp9CrsTcrRrSmupu92tHKLWmmhBCilN7uEaCfj+qb7efUjiPEPV1LyeCJeXtYeuAiFhp4q3t9Pn+iCXbWMj6qNKSZEkKIUnJ3sGbCI4EAfL7pDOeu31I5kRAFHYy9Qc8vd3Ao9ibOtpYseOYhnm9fS8ZHGYA0U0IIYQC9m3jTro4HWTk63lp1RCb1FCZl6f5Ynvh6D/GpmdT1cuS3l9rSoW5ltWOZDWmmhBDCADQaDVP7NMTWyoI955JYHnVJ7UhCkJ2rY8KvR3lj5RGycnWEN/Dil1FtqOHhoHY0syLNlBBCGIhvJXvGhdUFYOraE1xPzVQ5kajIEm5l8tT8vSze/TcAr4bVZe5TwTjaWKqczPxU+GYqPT0dPz8/XnvtNbWjCCHMwLA2/gRWdSb5djbvrTmudhxRQR25lEyvL3ew73wSjjaWzB/cnJc71cHCQsZHGUOFb6amTp1Ky5Yt1Y4hhDATlloLPuzXCAsN/PbXFbacilc7kqhgVh+6TP+vdnElOYOaHg6sfrENnQO91I5l1ip0M3XmzBlOnjxJ9+7d1Y4ihDAjDau7MKyNPwDvrDpKWmaOyolERZCTq2Pq2uOMXRpNZo6O0HqVWfViG2p7OqodzeyZbDMVGRlJz5498fb2RqPRsHr16gLrzJkzB39/f2xtbQkODmb79u3Feo7XXnuN6dOnGyixEEL865WwulRztePyzdt8FnFa7TjCzN1Mz+KZhfv5Zvt5AF4Krc38IS1wsbNSOVnFYLKj0NLS0mjcuDHPPPMM/fr1K/D40qVLGTt2LHPmzKFNmzZ8/fXXdOvWjePHj+Pr6wtAcHAwmZkFB4Bu3LiR/fv3U7duXerWrcuuXbsemCczMzPftlJSUgDIzs4mO9twFzi9sy1DblNtUpPpM7d6QP2arC1gcs/6PPf9Ib7beZ4eQV4EVXMu8fbUrscYpCbDOHU1lZFLorl44zZ2VhZ8+GgQ3YKqoMvNQZdbum2b83tkSBqlHEyGotFoWLVqFX369NEva9myJc2aNWPu3Ln6ZQEBAfTp06dIe5vGjx/PDz/8gFar5datW2RnZ/Pqq68yYcKEQtefNGkSkydPLrB8yZIl2NvLFPxCiMItOm3BwUQLqjsojGuYi1bG/woDik7U8GOMBVk6DZVsFJ6tl0s1mfXgvtLT0xk4cCDJyck4O5f8H5z/KpfNVFZWFvb29ixfvpy+ffvq1xszZgzR0dFs27atWNtfuHAhR48e5ZNPPrnnOoXtmfLx8SEhIcFgbwbkdcwRERGEhYVhZWUeu2elJtNnbvWA6dSUcCuTrl/sJPl2Dm+E1+W5tjVKtB1TqceQpKaS0+kUZm6OYe62vMN6rWu6M3NAI9zsrQ36POb4HiUmJlK1alWDNlMme5jvfhISEsjNzcXLK//ZCV5eXly9etUoz2ljY4ONjU2B5VZWVkb5ATPWdtUkNZk+c6sH1K+pqpsVb3cP5PWVh/l8cwyPNK6Gj3vJ92arXY8xSE3Fk5KRzSs//8Wmk3lnig5v588bXetjqTXeMGhzeo+MUUe5bKbuuPt6QoqilOgaQ0OHDjVQIiGEKOix5tX55dAl9pxL4q1VR1g87CG5HpookZj4Wzz//QHOXU/DxtKCD/o1pG/T6mrHqvBM9my++/Hw8ECr1RbYCxUfH19gb5UQQqhNo9EwrW9DrC0t2H4mgV+jr6gdSZRDm05co+/snZy7noa3iy0rRrSWRspElMtmytramuDgYCIiIvItj4iIoHXr1iqlEkKIe6tZ2ZHRD9cGYMqa49xIy1I5kSgvdDqFLzed4bnFB0jNzOGhGu789nJbGlZ3UTua+IfJHua7desWMTEx+vvnz58nOjoad3d3fH19GTduHIMGDaJ58+aEhIQwb948YmNjGTFihIqphRDi3p5vX4vf/4rj1LVU3l97gk8fb6x2JGHibmXm8Nqyv1h/LO9IzOAQP97pEYi1ZbncF2K2TLaZOnDgAKGhofr748aNA2DIkCEsXLiQAQMGkJiYyJQpU4iLiyMoKIh169bh5+enVmQhhLgva0sLpj3akP5f7WLlwUs82qwabWp7qB1LmKi/E9MYvvgAp6/dwlprwZTeDXjiIV+1Y4lCmGwz1bFjRx40a8OoUaMYNWpUGSUSQojSC/ZzY1ArPxbv/pu3Vh1hw9j22Fpp1Y4lTEzk6eu8/NMhkm9n4+lkw9yngwn2c1M7lrgH2U8ohBBl7H/h9ajibMvfiel8vumM2nGECVEUhXmRZxm6YB/Jt7Np4uPK7y+3lUbKxEkzJYQQZczJ1oopvRsAMC/yHCfiUlROJEzB7axcxi6NZtq6k+gUeLx5dZa+0AovZ1u1o4kHKHYzNWzYMFJTUwssT0tLY9iwYQYJJYQQ5q5Lgyp0bVCFXJ3Cm78cIVdn8hejEEZ06UY6/b/axa/RV7C00DCldwM+7NcIG0s5BFweFLuZWrRoEbdv3y6w/Pbt2yxevNggoYQQoiKY3LsBTjaW/HXxJot3X1A7jlDJ7rOJ9Jq1k2NXUqjkYM0Pz7VkcEgNmdi1HClyM5WSkkJycjKKopCamkpKSor+68aNG6xbtw5PT09jZhVCCLPi5WzLG93qA/DxhlNcvlnwH1VhvhRFYdGuCzz97V6S0rJo4O3Mby+3pVXNSmpHE8VU5LP5XF1d0Wg0aDQa6tatW+BxjUbD5MmTDRpOCCHM3cCHfFl96DIH/r7BhNVHmT+kueyRqAAysnOZ8OtRlh24BECfJt5Mf7QRdtZyWK88KnIztWXLFhRF4eGHH2blypW4u7vrH7O2tsbPzw9vb2+jhBRCCHNlYaFh+qMN6f7FdjadjGfdkav0aFRV7VjCiK6lZPDC91FEX7yJhQbGdwvguXb+0kSXY0Vupjp06ADkzUTu4+ODhYWcCCiEEIZQx8uJkR1r88WmM0z87Rhta3vgYm/4K9sL9UX9fYMRP0RxPTUTFzsrZg1sSrs6ldWOJUqp2JN2+vn5cfPmTfbt20d8fDw6nS7f44MHDzZYOCGEqChGdazFmsNXOHc9jQ/Wn2T6ow3VjiQM7Od9sbz761GycxXqeTnxzeDm+FayVzuWMIBiN1O///47Tz31FGlpaTg5OeXbLanRaKSZEkKIErC10jK9b0MGzNvDT/ti6dPEm5YyENksZOXoeG/Ncb7f8zcA3YKq8MljjXGwMdmLkIhiKvaxuldffVU/19TNmze5ceOG/ispKckYGYUQokJoWbMSTz7kA8D4VUfIzMlVOZEoreupmTw9fy/f7/kbjQZe61KXOU81k0bKzBS7mbp8+TKjR4/G3l52TQohhKG92TUAD0cbzl1PY86Ws2rHEaVw5FIyvWbtYN+FJJxsLJk/uDkvPVxHBpqboWI3U+Hh4Rw4cMAYWYQQosJzsbdicq+8S83M2RrDmWsFrzghTN+v0Vfo/9Uu4pIzqFnZgdUvtaFTgJfasYSRFHs/Y48ePfjf//7H8ePHadiwIVZW+c846dWrl8HCCSFERdS9YRU61fdk08l4xv9yhGUvhKgdSRRRTq6OVRcs2Lr7KACdAzyZMaAJzrZydqY5K3YzNXz4cACmTJlS4DGNRkNurhzjF0KI0tBoNEzpE8SeGds48PcNftofy+PNZB4/U3cjLYsXlxxkV1zeQZ/RD9dmbOe6WFjIYT1zV+zDfDqd7p5f0kgJIYRhVHO147XwegB8sO4k11IyVE4k7ufk1RR6zd7BrrNJWFsozHqiMeO61JNGqoIo1cybGRnyyy2EEMYyOKQGjau7kJqZw3trT6odR9zD+qNxPDpnFxeTbuPjZscrQbmEN5DxURVJsZup3Nxc3nvvPapVq4ajoyPnzp0D4N133+Xbb781eEAhhKiotBYapj/aCK2Fhg3H4zmSJHs5TIlOpzBj4ylG/HCQ9Kxc2tb24JcRrfB2UDuZKGvFbqamTp3KwoUL+eijj7C2ttYvb9iwIfPnzzdoOCGEqOgCvZ15vn1NAJaftyA2KR1FUVROJVIzsnn++yi+2BwDwLNt/Vn4TAtc5TJAFVKxB6AvXryYefPm0alTJ0aMGKFf3qhRI06elN3QQghhaGM61WHt4SvEJt2m02c78HK2IdjPjWa+bgT7udHA2wVrS7lealm5kJDG8MUHOBN/C2tLC6b3bUi/4OoAZOtk7HBFVOxm6vLly9SuXbvAcp1OR3Z2tkFCCSGE+JetlZYvBjRm7Pe7uZRuwbWUTNYducq6I1cBsLG0oHF1V5r5uf3TZLlSydFG5dTmadvp67y85CApGTl4Odswb1BzGvu4qh1LqKzYzVSDBg3Yvn07fn5++ZYvX76cpk2bGiyYEEKIfzXwduaVhrmEdu7MiWtpRMXe4ODfN4j6+wY30rPZdyGJfRf+vaSXv4eDfs9VsJ8bdTwd5cyyUlAUhW+2n+ODP06iU6CZrytfPR2Mp7Ot2tGECSh2MzVx4kQGDRrE5cuX0el0/PLLL5w6dYrFixezZs0aY2QUQgjxDztrLS1rVtJfBFlRFM4lpBH197/N1Zn4W5xPSON8QhorD14CwMnWkqa+bgT7utG8hhuNfVxxlOvDFUlGdi5vrjzM6ugrAAxo7sOUPg2wsdSqnEyYimL/JvXs2ZOlS5cybdo0NBoNEyZMoFmzZvz++++EhYUZI6MQQoh70Gg01KrsSK3KjjzePO8iycnp2Ry8+G9zFX3xJqkZOUSevk7k6esAWGigfhVn/Z6rYD83qrvZyXXj7nLl5m1e+D6KI5eT0VpomNgzkEGt/OR1EvmU6N+S8PBwwsPDDZ1FCCGEAbjYWxFaz5PQep5A3iVOTl5N5WBsXnN14MINLt+8zfG4FI7HpfD9nr8BqOxkQ/A/hwa7N6pKNVc7NctQ3f4LSYz8IYqEW1m4O1gze2AzQmpVUjuWMEGyj1cIIcycpdaCoGouBFVzYXBIDQCuJmfom6uov29w7Eoy11MzWX/sKuuPXWXmn6d5r08Qjzarrm54lSzZG8vE346SnasQUNWZeYOC8XG3VzuW+cq+Db++BO3GgVcDtdMUW5GaKXd3d06fPo2Hhwdubm733b2ZlJR0z8eEEEKYhioutnRvWJXuDasCeeOCjlxOJurvG/xx9Cp/XbzJuGV/EXn6Ou/1CcKpglyoNytHx5Q1x/hhTywAPRpV5eP+jbC3ln0PRhX5MRxdAZf2w8sHQVu+Xu8ipf3ss89wcnICYObMmcbMI4QQQgW2Vlpa1HCnRQ13hreryZwtMczcdIbV0Vc4GHuTz59oQlNfN7VjGlXCrUxG/XiQfeeT0GjgtS71GNWxloyPMrb4k7Dzi7zb4dPKXSMFRWymhgwZUuhtIYQQ5kdroeHlTnVoXbsSo3+KJjYpnce+2s24LnUZ0b6WWU6xcPRyMs8vPsCV5AycbCz5/MkmPFxfrq9ndDodrHkFdNlQrzsEPKJ2ohIpUjOVkpJS5A06OzuXOExZO3/+PMOGDePatWtotVr27NmDg4NcVEkIIQCC/dxZN6Ydb686wprDcXy0/hQ7ziTw2YAmeJnR/Eq/Rl/mjZWHycjWUdPDgXmDm1Pb01HtWBVD9I8Quwus7KHbh2qnKbEiNVOurq5F3s2Zm1t+ptIfOnQo77//Pu3atSMpKQkbG5kxWAgh/svFzoovn2xK+7qVmfjrMXadTaTrzEg+7t+YzoHle89Nrk7h4w2n+GrbWQBC61Vm5hNNcbGrGOPDVJeWCBHv5t3uOB5cfdXNUwpFaqa2bNmiv33hwgXefPNNhg4dSkhICAC7d+9m0aJFTJ8+3TgpjeDYsWNYWVnRrl07IG+QvRBCiII0Gg2PN/ch2M+N0T8d4tiVFJ5bfIAhIX6M7x6ArVX5m7wy+XY2Y34+xNZTefNujexYi9e61ENrhocwTVbEu3D7BngFQauRaqcplSJdGbNDhw76r8WLFzNjxgymT59Or1696NWrF9OnT+eTTz5hwYIFBgsWGRlJz5498fb2RqPRsHr16gLrzJkzB39/f2xtbQkODmb79u1F3v6ZM2dwdHSkV69eNGvWjGnTphksuxBCmKNalR35ZVRrnmvrD8Ci3X/TZ/ZOzlxLVTlZ8cTEp9Jn9k62nrqOrZUFXzzZlDe61pdGqixd2JF3iA8NPDITtOV7b2Cxh8zv3r2br776qsDy5s2b89xzzxkkFEBaWhqNGzfmmWeeoV+/fgUeX7p0KWPHjmXOnDm0adOGr7/+mm7dunH8+HF8ffN2FQYHB5OZmVngezdu3Eh2djbbt28nOjoaT09PunbtSosWLe45i3tmZma+bd0ZR5adnW3QCzzf2ZY5XTRaajJ95lYPmF9NplKPBfBGeB1Carrx+sqjnLyayiNf7uCtbvV4skX1Yp35pkZNm07G8+qKI6Rl5uLtYsucgU1o4O1ssAym8j4ZilHqycnE8vexaIDcZkPQVWkCZfh6GeO90SiKohTnG+rVq8cjjzzCp59+mm/5q6++ypo1azh16pRBA0LeLuZVq1bRp08f/bKWLVvSrFkz5s6dq18WEBBAnz59inS4cffu3UyePJn169cD8PHHHwPwv//9r9D1J02axOTJkwssX7JkCfb2MpGbEKLiScmCJWctOHEz7yBHI3cdT9TU4WCCOxkUBSIua1h30QIFDbWcFJ6pl4uTCWY1d3Wv/kZA3AoyLJ3ZHPAh2ZZle+JXeno6AwcOJDk52WAnzRV7z9Rnn31Gv3792LBhA61atQJgz549nD17lpUrVxok1INkZWURFRXFm2++mW95ly5d2LVrV5G20aJFC65du8aNGzdwcXEhMjKSF1544Z7rjx8/nnHjxunvp6Sk4OPjQ5cuXQx6BmN2djYRERGEhYVhZWUev+VSk+kzt3rA/Goy1Xoe1yks3P03n0Sc4XCSBfE5dnzSvyEt/R88DrWsakpMy2Ly7yf44+I1AJ56yIe3u9fDSlukkS7FYqrvU0kZvJ4b57Gc9zwAlj0+Iiyof+m3WUyJiYkG32axm6nu3btz5swZ5syZw8mTJ1EUhd69ezNixAh8fHwMHrAwCQkJ5Obm4uWV/0wSLy8vrl69WqRtWFpaMm3aNNq3b4+iKHTp0oVHHrn3/BY2NjaFnu1nZWVllF8YY21XTVKT6TO3esD8ajLFel7oWIc2dTwZ/dMhziWkMXjBAV4Krc3oTnWwLELDYuiaFEXh7PVbRByPZ9OJa0TF3kBRwEqrYUrvIJ58yPhnjZni+1QaBqlHUWDDG5CTATU7YtnkCVBhQlRjvC8lmma0evXqJjFg++5j84qiFOt4fbdu3ejWrZuhYwkhRIUTVM2F319uy6TfjrE86hJfbI5h59lEZg5oUibXtMvJ1bH/wg3+PHGNTSeucSExPd/jDau5MLFnIM1ryJnbqjm6Es5uBq0N9JihSiNlLCWesz09PZ3Y2FiysrLyLW/UqFGpQz2Ih4cHWq22wF6o+Pj4AnurhBBClA0HG0s+fqwx7etW5q1fjhD19w26f7GdaX0b0rOxt8GfLyUjm22nrrPpxDW2nLpO8u1/BxZbay0IqVWJzoFedKrviberncGfXxTD7Zuwfnze7XavQqVaqsYxtGI3U9evX+eZZ57hjz/+KPTxspi009ramuDgYCIiIujbt69+eUREBL179zb68wshhLi3no29aeLjypifD3Ew9iYv/3SI7WeuM6lXg1JfMPhiUvo/e5/i2XMukRzdv+dQudlb8XB9L8ICPWlbpzKONuXvGm9ma/N7kBYPlepA27FqpzG4Yv+kjR07lhs3brBnzx5CQ0NZtWoV165d4/333y9whl9p3Lp1i5iYGP398+fPEx0djbu7O76+vowbN45BgwbRvHlzQkJCmDdvHrGxsYwYMcJgGYQQQpSMj7s9y14I4YtNZ/hySwzLDlziwIUbfPFkU4KquRR5Ozqdwl+XbuobqJNX889pVauyA50DvQgL8KKpr5vMFWWKLkXB/m/zbj8yAyzN72ojxW6mNm/ezK+//kqLFi2wsLDAz8+PsLAwnJ2dmT59Oj169DBIsAMHDhAaGqq/f+dMuiFDhrBw4UIGDBhAYmIiU6ZMIS4ujqCgINatW4efn59Bnl8IIUTpWGotGNelHq1re/DK0mjOJaTRd85O3uhan2Ft/O/5fbezctkRk8Cfx6+x6WQ8Cbf+nePPQgMtargTFuhFpwAv/D3keqomLTcH1owBFGj8JPi3VzuRURS7mUpLS8PT0xPIuwTL9evXqVu3Lg0bNuTgwYMGC9axY0ceNAXWqFGjGDVqlMGeUwghhOG1qlmJP8a0442Vh9lw7Brvrz3B9jMJfNA3UL9OfEoGm07mnX23/UwCmTk6/WOONpZ0qFeZzgGedKzriZuDtRpliJLY+xVcPQK2rtDlfbXTGE2xm6l69epx6tQpatSoQZMmTfj666+pUaMGX331FVWrVjVGRiGEEOWcq701Xz0dzJJ9sUz5/TjbTl/nkVm7aepiwbdf7+HwpZR861dztftn75MnLf0rYW1p+DmhhJElX4It/5z5HzYFHDzUzWNEJRozFRcXB8DEiRMJDw/nxx9/xNramoULFxo6nxBCCDOh0Wh4qqUfLWq4M/qnQ5y8msqfaRZAXiPV2MeVzvU96RzoRf0qTsWa6kaYoD/egOw08GkFTQepncaoit1MPfXUU/rbTZs25cKFC5w8eRJfX188PMy36xRCCGEYdb2cWP1iG2ZtOs3OIzH0axtElwZV8XS2VTuaMJST6+DkGrCwhJ4zwcK89ywWq7rs7Gxq1qzJ8ePH9cvs7e1p1qyZNFJCCCGKzNZKy5hOtRlaV8eA5tWlkTInmbdg3T/XuW39MngGqJunDBSrmbKysiIzM1N2vQohhBCicFunQ8olcPWF9q+rnaZMFHu/28svv8yHH35ITk6OMfIIIYQQory6egT2zM273f1TsDb+pYRMQbHHTO3du5dNmzaxceNGGjZsiIND/jk+fvnlF4OFE0IIIUQ5odPBmldAyYXA3lC3i9qJykyxmylXV1f69etnjCxCCCGEKK+iFsCl/WDtBF0/VDtNmSp2M7VgwQJj5BBCCCFEeZV6Df6cnHe707vgXLHmnTTvcxWFEEIIYXwb34bMZKjaBFo8p3aaMlfsPVNNmzYt9Gw+jUaDra0ttWvXZujQofmuqyeEEEIIM3V2MxxZDhqLf+aU0qqdqMwVe89U165dOXfuHA4ODoSGhtKxY0ccHR05e/YsLVq0IC4ujs6dO/Prr78aI68QQgghTEV2Bqx9Ne/2Q8+Dd1N186ik2HumEhISePXVV3n33XfzLX///ff5+++/2bhxIxMnTuS9996jd+/eBgsqhBBCCBOz/VNIOgdOVSH0bbXTqKbYe6aWLVvGk08+WWD5E088wbJlywB48sknOXXqVOnTCSGEEMI0XT8NOz7Lu931A7B1VjePiordTNna2rJr164Cy3ft2oWtbd7lAHQ6HTY2NqVPJ4QQQgjToyiwdhzosqFOl7x5pSqwYh/me/nllxkxYgRRUVG0aNECjUbDvn37mD9/Pm+99RYAGzZsoGnTinncVAghhDB7f/0MF7aDpR10/wQq+GXmit1MvfPOO/j7+zNr1iy+//57AOrVq8c333zDwIEDARgxYgQjR440bFIhhBBCqC89KW8qBICOb4Cbn7p5TECxmymAp556iqeeeuqej9vZ2ZU4kBBCCCFMWMQESE+EygEQ8pLaaUyCTNophBBCiKL5ezccyjsqRc+ZoLVSNY6pkGZKCCGEEA+Wk5V3IWOAZoPBt5W6eUyINFNCCCGEeLDds+D6CbD3gM6T1U5jUorUTKWkpBg7hxBCCCFM1c2/YdtHebfDp4K9u7p5TEyRmik3Nzfi4+MBePjhh7l586YxMwkhhBDCVCgK2vVvQM5tqNEOGg1QO5HJKVIz5ejoSGJiIgBbt24lOzvbqKGEEEIIYRqq3tyPxdk/QWsNj3xW4eeUKkyRpkbo3LkzoaGhBAQEANC3b1+sra0LXXfz5s2GSyeEEEII9WSm0vDyj3m3274CHnXUzWOiitRM/fDDDyxatIizZ8+ybds2GjRogL29vbGzCSGEEEJFFlunYZd9A8W9Jpq249SOY7KK1EzZ2dkxYsQIAA4cOMCHH36Iq6urMXMJIYQQQk2XD2JxYD4AuV0/xtLKVuVApqvYM6Bv2bJFf1tRFAA0cvxUCCGEMB+6XFgzFg0KF91CqOLfQe1EJq1E80wtXryYhg0bYmdnh52dHY0aNdJfp688+eyzz2jQoAGBgYGMHj1a3xwKIYQQFdq+byDuLxRbF45VG6h2GpNX7D1TM2bM4N133+Wll16iTZs2KIrCzp07GTFiBAkJCbzyyivGyGlw169fZ9asWRw7dgwrKyvat2/Pnj17CAkJUTuaEEIIoZ6UK7D5fQB0oe+SedVF5UCmr9jN1JdffsncuXMZPHiwflnv3r1p0KABkyZNKjfNFEBOTg4ZGRkAZGdn4+npqXIiIYQQQmV/vAFZqVC9Bbqmg+GP9WonMnnFPswXFxdH69atCyxv3bo1cXFxBgkFEBkZSc+ePfH29kaj0bB69eoC68yZMwd/f39sbW0JDg5m+/btRd5+5cqVee211/D19cXb25vOnTtTq1Ytg+UXQgghyp3TG+DEb6DRwiMzQSNXnSuKYu+Zql27NsuWLeOtt97Kt3zp0qXUqWO4+SfS0tJo3LgxzzzzDP369Svw+NKlSxk7dixz5syhTZs2fP3113Tr1o3jx4/j6+sLQHBwMJmZmQW+d+PGjdjZ2bFmzRouXLiAnZ0d3bp1IzIykvbt2xeaJzMzM9+27lxiJzs726CTmN7ZljlNjCo1mT5zqwfMryZzqwekJpOTnY7l2tfQALktR6CrVK9813MPxqhFoxRz1PXKlSsZMGAAnTt3pk2bNmg0Gnbs2MGmTZtYtmwZffv2NXxIjYZVq1bRp08f/bKWLVvSrFkz5s6dq18WEBBAnz59mD59+gO3uXz5crZu3crs2bMB+Pjjj1EUhddff73Q9SdNmsTkyQUv7LhkyRKZc0sIIUS5F3h5KXXi15JuVYnNAR+Qq7VRO5JRpKenM3DgQJKTk3F2djbINou9Z6pfv37s3buXzz77jNWrV6MoCoGBgezbt4+mTZsaJNSDZGVlERUVxZtvvplveZcuXdi1a1eRtuHj48OuXbvIyMjAysqKrVu38vzzz99z/fHjxzNu3L8TlqWkpODj40OXLl0M9mZAXsccERFBWFgYVlZWBtuumqQm02du9YD51WRu9YDUZFLiT2D51wYArPt8TnjdrkA5ruc+7lwez5CK3UxB3uGzH374wdBZiiwhIYHc3Fy8vLzyLffy8uLq1atF2karVq3o3r07TZs2xcLCgk6dOtGrV697rm9jY4ONTcEu3crKyig/YMbarpqkJtNnbvWA+dVkbvWA1KQ6nQ7Wvwa6HKj/CJYNehZYpVzV8wDGqKNEzZSpuHuyUEVRijWB6NSpU5k6daqhYwkhhBDlx6Hv4eJesHaEbh+qnaZcKpfD9D08PNBqtQX2QsXHxxfYWyWEEEKIe7h1HSIm5N0OfQtcqqubp5wql82UtbU1wcHBRERE5FseERFR6LQNQgghhCjExncg4yZUaQgPvaB2mnLLZA/z3bp1i5iYGP398+fPEx0djbu7O76+vowbN45BgwbRvHlzQkJCmDdvHrGxsfoLMgshhBDiPs5tg8M/Axp45HPQmmxLYPKK9crl5ORga2tLdHQ0QUFBxsoEwIEDBwgNDdXfv3Mm3ZAhQ1i4cCEDBgwgMTGRKVOmEBcXR1BQEOvWrcPPz8+ouYQQQohyLycT1v5zhnqLZ6F6sLp5yrliNVOWlpb4+fmRm5trrDx6HTt2fOCFh0eNGsWoUaOMnkUIIYQwKztmQmIMOHpBpwlqpyn3ij1m6p133mH8+PEkJSUZI48QQgghjCnxLGz/NO921+lgKxcyLq1iHyD94osviImJwdvbGz8/PxwcHPI9fvDgQYOFE0IIIYQBKQqseQVyM6FWJ2jwqNqJzEKxm6n/XtJFCCGEEOXIkRVwfhtY2kKPT6AYczOKeyt2MzVx4kRj5BBCCCGEMd2+ARvG591u/xq411Q3jxkp8XmQUVFRnDhxAo1GQ2BgYJldl08IIYQQJfDnZEi7Dh71oPUYtdOYlWI3U/Hx8TzxxBNs3boVV1dXFEUhOTmZ0NBQfv75ZypXrmyMnEIIIYQoqYv7IGpB3u1HPgNLa3XzmJlin8338ssvk5KSwrFjx0hKSuLGjRscPXqUlJQURo8ebYyMQgghhCip3Gz4fWze7SZPQ402qsYxR8XeM7V+/Xr+/PNPAgIC9MsCAwOZPXs2Xbp0MWg4IYQQQpTSnrkQfwzs3CFsitppzFKx90zpdDqsrKwKLLeyskKn0xkklBBCCCEM4GYsbJ2ed7vLe+BQSd08ZqrYzdTDDz/MmDFjuHLlin7Z5cuXeeWVV+jUqZNBwwkhhBCihBQF1r0O2eng1waaPKV2IrNV7GZq1qxZpKamUqNGDWrVqkXt2rXx9/cnNTWVL7/80hgZhRBCCFFcJ9fA6T/Awipv0LnMKWU0xR4z5ePjw8GDB4mIiODkyZMoikJgYCCdO3c2Rj4hhBBCFFdmKvzxRt7tNqOhcj1185i5YjVTOTk52NraEh0dTVhYGGFhYcbKJYQQQoiS2jIdUi6DWw1o/z+105i9Yh3ms7S0xM/Pj9zcXGPlEUIIIURpxP0Fe+fm3e7xKVjZqZunAij2mKl33nmH8ePHk5SUZIw8QgghhCgpXW7enFKKLu8ixrVlCE5ZKPaYqS+++IKYmBi8vb3x8/PDwcEh3+MHDx40WDghhBBCFMOB7+DKQbBxhq7T1U5TYRS7merTp48RYgghhBCiVFKvwqZ/JuXsNAGcqqibpwIp9gB0gGHDhuHj42OUQEIIIYQogfXjITMFvJtB82Fqp6lQij0A/ZNPPpEB6EIIIYQpifkTjv0CGgvoORMstGonqlCKPQC9U6dObN261QhRhBBCCFFs2bdh7at5t1uOhKqN1c1TARV7zFS3bt0YP348R48eJTg4uMAA9F69ehksnBBCCCEeIPITuHEBnKtB6Hi101RIxW6mRo4cCcCMGTMKPKbRaOQQoBBCCFFWrp+CnZ/n3e72Idg4qZungip2M6XT6YyRQwghhBDFoSiw5hXQZUPdblD/EbUTVVjFHjMlhBBCCBMQ/SP8vROs7KH7R3IhYxUVuZnq3r07ycnJ+vtTp07l5s2b+vuJiYkEBgYaNJwQQgghCpGWCBvfzbvd8U1w9VU3TwVX5GZqw4YNZGZm6u9/+OGH+S4pk5OTw6lTpwybTgghhBAFRUyA20ng2QBajVI7TYVX5GZKUZT73hdCCCFEGbiwE6J/yLvdcyZorVSNI2TMlBBCCFF+5GTlDToHCH4GfB5SN48AitFMaTQaNHcNbrv7vqnq27cvbm5u9O/fv8Bja9asoV69etSpU4f58+erkE4IIYQool1fQMIpcKgMnSeqnUb8o8hTIyiKwtChQ7GxsQEgIyODESNG6Cft/O94KlMzevRohg0bxqJFi/Itz8nJYdy4cWzZsgVnZ2eaNWvGo48+iru7u0pJhRBCiHtIOgeRH+fdDp8Gdm7q5hF6RW6mhgwZku/+008/XWCdwYMHlz6REYSGhhZ6CZx9+/bRoEEDqlWrBuSdsbhhwwaefPLJMk4ohBBC3IeiwNrXICcDanaEho+pnUj8R5GbqQULFhglQGRkJB9//DFRUVHExcWxatUq+vTpk2+dOXPm8PHHHxMXF0eDBg2YOXMm7dq1K/VzX7lyRd9IAVSvXp3Lly+XertCCCGEQR37Bc5uAq0N9Jghc0qZGNUHoKelpdG4cWNmzZpV6ONLly5l7NixvP322xw6dIh27drRrVs3YmNj9esEBwcTFBRU4OvKlSv3fe7CzkgsL+PAhBBCVBAZybD+n2vutRsHlWqpm0cUUOzLyRhat27d6Nat2z0fnzFjBs8++yzPPfccADNnzmTDhg3MnTuX6dOnAxAVFVWi565WrVq+PVGXLl2iZcuWha6bmZmZb1xYSkoKANnZ2WRnZ5fo+QtzZ1uG3KbapCbTZ271gPnVZG71gNRUVBYRk9HeuobiXoucli9BGb5e5vweGZJGMaEJozQaTb7DfFlZWdjb27N8+XL69u2rX2/MmDFER0ezbdu2Im9769atzJo1ixUrVuiX5eTkEBAQwNatW/UD0Pfs2UOlSpUKfP+kSZOYPHlygeVLlizB3t6+GFUKIYQQReOadpb2p6egQWFn7TdJcJIrjZRWeno6AwcOJDk5GWdnZ4NsU/U9U/eTkJBAbm4uXl5e+ZZ7eXlx9erVIm8nPDycgwcPkpaWRvXq1Vm1ahUtWrTA0tKSTz/9lNDQUHQ6Ha+//nqhjRTA+PHjGTdunP5+SkoKPj4+dOnSxWBvBuR1zBEREYSFhWFlZR4TsUlNps/c6gHzq8nc6gGp6YF0OVh+F4YGBV3Dx3mo12uGCVkM5vgeJSYmGnybJt1M3XH3OCZFUYo1tmnDhg33fKxXr1706tXrgduwsbHRTwvxX1ZWVkb5ATPWdtUkNZk+c6sHzK8mc6sHpKZ72v0NXDsCtq5YhE/DQsXXyJzeI2PUofoA9Pvx8PBAq9UW2AsVHx9fYG+VEEIIYTaSL8OWqXm3wyaDY2V184j7MulmytramuDgYCIiIvItj4iIoHXr1iqlEkIIIYzsj9ch6xb4tIKmpjmHo/iX6of5bt26RUxMjP7++fPniY6Oxt3dHV9fX8aNG8egQYNo3rw5ISEhzJs3j9jYWEaMGKFiaiGEEMJITv0BJ9eAhSU88hlYmPR+D4EJNFMHDhwgNDRUf//OIO8hQ4awcOFCBgwYQGJiIlOmTCEuLo6goCDWrVuHn5+fWpGFEEII48hKg3X/y7sd8hJ4ydl75YHqzVTHjh0LnTzzv0aNGsWoUaPKKJEQQgihkq0fQPJFcPGFDq+rnUYUkew7FEIIIUzB1aOwe3be7R6fgLWDunlEkUkzJYQQQqhNp4M1Y0HJhYBeUDdc7USiGKSZEkIIIdR2cBFc2g/WjtDtQ7XTiGKSZkoIIYRQ0614+HNi3u2H3wFnb3XziGKTZkoIIYRQ04a3ISMZqjaGh55XO40oAWmmhBBCCLWc3QJHloHGAh6ZCRZatROJEpBmSgghhFBDdgasfTXvdovhUK2ZunlEiUkzJYQQQqhhx2eQdBYcq8DDb6udRpSCNFNCCCFEWUs4Aztm5N3u9gHYuqibR5SKNFNCCCFEWVIUWDsOcrOgdhgE9lE7kSglaaaEEEKIsnR4GZyPBEvbvJnONRq1E4lSkmZKCCGEKCvpSbDhrbzbHV4HtxqqxhGGIc2UEEIIUVb+nATpCVC5PoS8rHYaYSDSTAkhhBBlIXZv3mVjIG9OKUtrVeMIw5FmSgghhDC23Oy8CxkDNB0EfiGqxhGGJc2UEEIIYWy7Z0P8cbCvBGFT1E4jDEyaKSGEEMKYbvwNWz/Iu93lfbB3VzePMDhppoQQQghjURRY9z/IuQ012kHjJ9VOJIxAmikhhBDCWE78Dmc2gIUV9Jghc0qZKWmmhBBCCGPITIU/3si73XYsVK6rahxhPNJMCSGEEMaweSqkXgE3f2j3qtpphBFJMyWEEEIYWtxfsO/rvNuPzAArO3XzCKOSZkoIIYQwJEWH9o9XQdFBUH+o9bDaiYSRSTMlhBBCGJB/wiYs4qLBxgXCp6kdR5QBaaaEEEIIQ0mNI+DK8rzbnSeAk5e6eUSZsFQ7gBBCCGEutBHvYKHLQOcdjEXwMLXjiDIie6aEEEIIQzjzJxYnfkWHBbndPwUL+YitKOSdFkIIIUor+zasy5v+4FzlLuAVpHIgUZakmRJCCCFKa/uncOMCipM3p6r2VTuNKGMVopnq27cvbm5u9O/fP9/yixcv0rFjRwIDA2nUqBHLly9XKaEQQohyK+EM7JgJQG6XaeRoZU6piqZCNFOjR49m8eLFBZZbWloyc+ZMjh8/zp9//skrr7xCWlqaCgmFEEKUS4oCa8eBLhvqhKPU66F2IqGCCtFMhYaG4uTkVGB51apVadKkCQCenp64u7uTlJRUxumEEEKUW0eWw/lIsLSD7h/JhYwrKNWbqcjISHr27Im3tzcajYbVq1cXWGfOnDn4+/tja2tLcHAw27dvN3iOAwcOoNPp8PHxMfi2hRBCmKHbN2DDW3m3278GbjVUjSPUo/o8U2lpaTRu3JhnnnmGfv36FXh86dKljB07ljlz5tCmTRu+/vprunXrxvHjx/H19QUgODiYzMzMAt+7ceNGvL29H5ghMTGRwYMHM3/+/Huuk5mZme85UlJSAMjOziY7O/uBz1FUd7ZlyG2qTWoyfeZWD5hfTeZWD5T/miwiJqNNu47iUZech0bCfz4PymtNdzO3esA4tWgURVEMvtUS0mg0rFq1ij59+uiXtWzZkmbNmjF37lz9soCAAPr06cP06dOLvO2tW7cya9YsVqxYkW95ZmYmYWFhDB8+nEGDBt3z+ydNmsTkyZMLLF+yZAn29vZFziGEEKL8c007S/vTU9CgsKP2eBKdAtSOJIooPT2dgQMHkpycjLOzs0G2qfqeqfvJysoiKiqKN998M9/yLl26sGvXrlJvX1EUhg4dysMPP3zfRgpg/PjxjBs3Tn8/JSUFHx8funTpYrA3A/I65oiICMLCwrCysjLYdtUkNZk+c6sHzK8mc6sHynFNuhwsvwtDg4Ku4eO07PWq/qFyW9M9mFs9kHc0ytBMuplKSEggNzcXL6/81zby8vLi6tWrRd5OeHg4Bw8eJC0tjerVq7Nq1SpatGjBzp07Wbp0KY0aNdKP1fr+++9p2LBhgW3Y2NhgY2NTYLmVlZVRfsCMtV01SU2mz9zqAfOrydzqgXJY055v4doRsHXBInwaFoVkL3c1PYA51WOMOky6mbpDc9fZEYqiFFh2Pxs2bCh0edu2bdHpdKXKJoQQogJJiYPN7+fd7jwJHCurGkeYBtXP5rsfDw8PtFptgb1Q8fHxBfZWCSGEEEa3YTxkpUK15tBsqNpphIkw6WbK2tqa4OBgIiIi8i2PiIigdevWKqUSQghRIcVsgmOrQGMBj3wmFzIWeqof5rt16xYxMTH6++fPnyc6Ohp3d3d8fX0ZN24cgwYNonnz5oSEhDBv3jxiY2MZMWKEiqmFEEJUKNm3Ye0/A81bjoCqjdTNI0yK6s3UgQMHCA0N1d+/c8bckCFDWLhwIQMGDCAxMZEpU6YQFxdHUFAQ69atw8/PT63IQgghKpodn8GN8+DkDaFvqZ1GmBjVm6mOHTvyoKmuRo0axahRo8ookRBCCPEfCTF5zRRA1+lgU/DyZKJikwO+QgghxL3cuZBxbhbU7gyBvdVOJEyQNFNCCCHEvRxdCee3gaUtdP9YLmQsCiXNlBBCCFGY2zf/vZBxu9fAvaaqcYTpkmZKCCGEKMzm9+HWNahUB9qMVjuNMGHSTAkhhBB3u3wQ9s/Pu93jU7AseDkxIe6QZkoIIYT4L10urHkFUKDh41Czg9qJhImTZkoIIYT4r/3fQlw02LhA+FS104hyQJopIYQQ4o7Uq7D5vbzbnSeAo6e6eUS5IM2UEEIIcceGtyAzBbybQfAzaqcR5YQ0U0IIIQTA2c1580rpL2SsVTuRKCekmRJCCCGyM/69kPFDz4N3E1XjiPJFmikhhBBi50xIOgeOVSD0bbXTiHJGmikhhBAVW+JZ2D4j73bX6WDrrG4eUe5IMyWEEKLiUpS8w3u5mVDrYWjQV+1EohySZkoIIUTFdewXOLcFtDbQ/RO5kLEoEWmmhBBCVEwZybB+fN7tdq9CpVrq5hHlljRTQgghKqbNU/MuZOxeC9qOVTuNKMekmRJCCFHxXDkE+7/Juy0XMhalJM2UEEKIiuXOhYwVHQT1h1qhaicS5Zw0U0IIISqWA9/l7ZmycYbwaWqnEWZAmikhhBAVR+o12DQl73anCeDkpW4eYRakmRJCCFFxbHz7nwsZN4Xmw9ROI8yENFNCCCEqhnNb4chyuZCxMDhppoQQQpi/nMx/L2Tc4rm8PVNCGIg0U0IIIczfzs8hMQYcveDhd9ROI8yMNFNCCCHMW+JZiPwk73b4NLB1UTePMDvSTAkhhDBfGSmwfGjehYxrdoSgfmonEmZImikhhBDmKScLlj4NVw+DvQf0/FwuZCyMokI0U3379sXNzY3+/fsX+nh6ejp+fn689tprZZxMCCGEUeh0sHoknN8GVg7w1HJwq6F2KmGmKkQzNXr0aBYvXnzPx6dOnUrLli3LMJEQQgijingXjq4AC0sY8D1Ua6Z2ImHGKkQzFRoaipOTU6GPnTlzhpMnT9K9e/cyTiWEEMIodn0Ju2fl3e49B2p3UjePMHuqN1ORkZH07NkTb29vNBoNq1evLrDOnDlz8Pf3x9bWluDgYLZv326w53/ttdeYPn26wbYnhBBCRYeXwcZ/pj4Iew8aD1A3j6gQVG+m0tLSaNy4MbNmzSr08aVLlzJ27FjefvttDh06RLt27ejWrRuxsbH6dYKDgwkKCirwdeXKlfs+96+//krdunWpW7euQWsSQgihgphNeeOkAFq9CK1fVjePqDAs1Q7QrVs3unXrds/HZ8yYwbPPPstzzz0HwMyZM9mwYQNz587V71GKiooq0XPv2bOHn3/+meXLl3Pr1i2ys7NxdnZmwoQJBdbNzMwkMzNTfz8lJQWA7OxssrOzS/T8hbmzLUNuU21Sk+kzt3rA/Goyt3rAwDXFRWO5bBAaXQ66wL7kPjwRcnJKv91iMrf3ydzqAePUolEURTH4VktIo9GwatUq+vTpA0BWVhb29vYsX76cvn376tcbM2YM0dHRbNu2rcjb3rp1K7NmzWLFihWFPr5w4UKOHj3KJ598UujjkyZNYvLkyQWWL1myBHt7+yLnEEIIYVgOmddod3oKNjmpXHcMZE+tV9FZWKkdS5io9PR0Bg4cSHJyMs7OzgbZpup7pu4nISGB3NxcvLy88i338vLi6tWrRd5OeHg4Bw8eJC0tjerVq7Nq1SpatGhRrCzjx49n3Lhx+vspKSn4+PjQpUsXg70ZkNcxR0REEBYWhpWVefwxkJpMn7nVA+ZXk7nVAwaq6VY8lot7oMlJRfFqiOug3+hqU/gJR2XB3N4nc6sHIDEx0eDbNOlm6g7NXZOsKYpSYNn9bNiw4YHrDB069L6P29jYYGNjU2C5lZWVUX7AjLVdNUlNps/c6gHzq8nc6oFS1JSZCssGwo3z4OqH5umVWDm6Gz5gCZjb+2RO9RijDtUHoN+Ph4cHWq22wF6o+Pj4AnurhBBCVCA5WbBsMMRFg30lePoXcJLPBaEOk26mrK2tCQ4OJiIiIt/yiIgIWrdurVIqIYQQqtLp4NcX4exmsLKHgcvBo7baqUQFpvphvlu3bhETE6O/f/78eaKjo3F3d8fX15dx48YxaNAgmjdvTkhICPPmzSM2NpYRI0aomFoIIYRq/pwIR5aBRguPL4bqwWonEhWc6s3UgQMHCA0N1d+/M8h7yJAhLFy4kAEDBpCYmMiUKVOIi4sjKCiIdevW4efnp1ZkIYQQatk9G3Z9kXe79yyoE6ZuHiEwgWaqY8eOPGh2hlGjRjFq1KgySiSEEMIkHVkBG97Ku91pIjQZqG4eIf5h0mOmhBBCCADObYVV/wzveOgFaPuKqnGE+C9ppoQQQpi2uL/g56dBlw0N+kLXD6AY0+MIYWzSTAkhhDBdSefhh/6QlQo12kHfr8FCPrqEaZGfSCGEEKbp1nX44VFIiwevIHjiR7AsOHmyEGqTZkoIIYTpybwFSx6HpHPg4gtPrQBbF7VTCVEoaaaEEEKYltxsWD4ErhwEO3cY9As4V1U7lRD3JM2UEEII06Eo8NvLEPMnWNrBwGXgUUftVELclzRTQgghTMemyfDXT3mzmz+2EHxaqJ1IiAeSZkoIIYRp2PMV7Pgs73bPz6FeV3XzCFFE0kwJIYRQ39FfYP2bebcffgeaDVI3jxDFIM2UEEIIVWkubIdVLwAKtHgO2r2mdiQhikWaKSGEEKpxTo9Fu2Iw5GZBQE/o9pHMbi7KHdUvdCzuknYdu6wEyEwFK3e104h7uX0z731KvgiWRv41cq4GFlrjPkdZSk+CrFvGf56cXFB0xn8ec5SVBumJxn+elHhCzn6CJicV/NrAo/PN62ddVBjSTJkY7dpX6HJmPTl+GnhomNpxRGHOb8dycW+6KLlwrAyez68tPLO2DJ6oDJxcB0ufKpMmxwp4yKUZ8IjRn8uspF6FL5vnXb7FyKz++VIqB6B5YglY2Rr9OYUwBmmmhCiuq4fRKLkoaMDSBqMdkFB0eYc+rhw01jOUvbjovLo0FqC1Nt7z/PPauaafN95zmKuE0/82UpbGbW4U4IZ1NZyeWIaVnatRn0sIY5JmymQpagcQD3DJLYQqo37DysrKOE9w42/4vJFxtq225s9Cj0+Mt/24w/B1O+NtvyKoHAAv7jHqU+RkZ7N93Tq6y+zmopyTAeimRgZemj6ljBvdsn4+YyrjWjTm9NoJIUyWNFNCCCH+JQ2oEMUmzZSpkj9oQpSc7OEVQpQhaaZMjnwImL4yanT1DYE5Ndb/1FJmzY45vXZlTBpSIYpMmikhhBD/IQ2oEMUlzZSJ0sgftHJA/nM3XfLeCCHKjjRTpkZ2rZu+MhvPpinj5ysD+lrk59z0yXskRFFJMyVECSnyWWO65J8SIUQZkmbKVJnT3gghRPkhf3uEKDZppkyO/Edt+uRsvpKTs/nKDdm7J0SRSTMlRInJh43pkvdGCFF2pJkyWfIftRBCDfK3R4jikmbK1MiuddMnZ/OVXBmfzSdTjJSG/C0SoqikmRKixOTDxmTJPyVCiDJkqXaA8kr55z/slJQUg25Xl56NRaZC7q3baA28bbVkZ2eTnp5OSkoKVlZWascpvbQMyFRIzcjGwZg1paRCpgIaHRj5Z6HM3qN/XjvSM41bU+otyFTIzNFhYSY/d2X2HqWm5b1Ht3PM5+euDJlbTeZWD0Bqairw7+e4IWgUQ26tArl06RI+Pj5qxxBCCCFECZw9e5aaNWsaZFvSTJWQTqfjypUrODk5oTHgIYWUlBR8fHy4ePEizs7OBtuumqQm02du9YD51WRu9YDUVB6YWz0AycnJ+Pr6cuPGDVxdXQ2yTTnMV0IWFhZUr17daNt3dnY2mx/cO6Qm02du9YD51WRu9YDUVB6YWz2Q9zlusG0ZbEtCCCGEEBWQNFNCCCGEEKUgzZSJsbGxYeLEidjY2KgdxWCkJtNnbvWA+dVkbvWA1FQemFs9YJyaZAC6EEIIIUQpyJ4pIYQQQohSkGZKCCGEEKIUpJkSQgghhCgFaaaEEEIIIUpBmikTceHCBZ599ln8/f2xs7OjVq1aTJw4kaysrHzrxcbG0rNnTxwcHPDw8GD06NEF1jElU6dOpXXr1tjb299zptn9+/fTqVMnXF1dcXNzo0uXLkRHR5dpzqIqSj0ACxcupFGjRtja2lKlShVeeumlsgtZTEWtCSAxMZHq1auj0Wi4efNmmeQriQfV9Ndff/Hkk0/i4+ODnZ0dAQEBfP7552UftIiK8h6Vt78Ndzt9+jS9e/fGw8MDZ2dn2rRpw5YtW9SOVWpr166lZcuW2NnZ4eHhwaOPPqp2JIPIzMykSZMmaDQak/17/SBF/dwtCmmmTMTJkyfR6XR8/fXXHDt2jM8++4yvvvqKt956S79Obm4uPXr0IC0tjR07dvDzzz+zcuVKXn31VRWT319WVhaPPfYYI0eOLPTx1NRUwsPD8fX1Ze/evezYsQNnZ2fCw8PJzs4u47QP9qB6AGbMmMHbb7/Nm2++ybFjx9i0aRPh4eFlmLJ4ilLTHc8++yyNGjUqg1Sl86CaoqKiqFy5Mj/88APHjh3j7bffZvz48cyaNauMkxbNg+opj38b7tajRw9ycnLYvHkzUVFRNGnShEceeYSrV6+qHa3EVq5cyaBBg3jmmWf466+/2LlzJwMHDlQ7lkG8/vrreHt7qx2jVIryuVtkijBZH330keLv76+/v27dOsXCwkK5fPmyftlPP/2k2NjYKMnJyWpELLIFCxYoLi4uBZbv379fAZTY2Fj9ssOHDyuAEhMTU4YJi+de9SQlJSl2dnbKn3/+WfahSuleNd0xZ84cpUOHDsqmTZsUQLlx40aZZSupB9X0X6NGjVJCQ0ONG6iU7lVPef7boCiKcv36dQVQIiMj9ctSUlIUoFz+LimKomRnZyvVqlVT5s+fr3YUg1u3bp1Sv3595dixYwqgHDp0SO1IBnP3525RyZ4pE5acnIy7u7v+/u7duwkKCsr330B4eDiZmZlERUWpEbHU6tWrh4eHB99++y1ZWVncvn2bb7/9lgYNGuDn56d2vGKLiIhAp9Nx+fJlAgICqF69Oo8//jgXL15UO1qpHD9+nClTprB48WKDXs/KlNz9+1aelPe/DZUqVSIgIIDFixeTlpZGTk4OX3/9NV5eXgQHB6sdr0QOHjzI5cuXsbCwoGnTplStWpVu3bpx7NgxtaOVyrVr1xg+fDjff/899vb2ascxuJL+HTDPv4pm4OzZs3z55ZeMGDFCv+zq1at4eXnlW8/NzQ1ra+tyuyvcycmJrVu38sMPP2BnZ4ejoyMbNmxg3bp1WFqWv+twnzt3Dp1Ox7Rp05g5cyYrVqwgKSmJsLCwcjV+5b8yMzN58skn+fjjj/H19VU7jlHs3r2bZcuW8cILL6gdpUTK+98GjUZDREQEhw4dwsnJCVtbWz777DPWr1//wHF8purcuXMATJo0iXfeeYc1a9bg5uZGhw4dSEpKUjldySiKwtChQxkxYgTNmzdXO47BFfa5W1TSTBnZpEmT0Gg09/06cOBAvu+5cuUKXbt25bHHHuO5557L95hGoynwHIqiFLrcWEpS073cvn2bYcOG0aZNG/bs2cPOnTtp0KAB3bt35/bt20auJI8h69HpdGRnZ/PFF18QHh5Oq1at+Omnnzhz5kyZDqY1ZE3jx48nICCAp59+2sip78+QNf3XsWPH6N27NxMmTCAsLMwIyQtn6HpM4W/D3Ypao6IojBo1Ck9PT7Zv386+ffvo3bs3jzzyCHFxcarlL0xRa9LpdAC8/fbb9OvXj+DgYBYsWIBGo2H58uUqV5FfUWv68ssvSUlJYfz48WpHvi9Df+4WRfn717+ceemll3jiiSfuu06NGjX0t69cuUJoaCghISHMmzcv33pVqlRh7969+ZbduHGD7OzsAv+VGlNxa7qfJUuWcOHCBXbv3q0/fLRkyRLc3Nz49ddfH/g8hmDIeqpWrQpAYGCgflnlypXx8PAgNja2xBmLy5A1bd68mSNHjrBixQog7wMawMPDg7fffpvJkyeXKmtRGbKmO44fP87DDz/M8OHDeeedd0qRrvgMWY+p/G24W1Fr3Lx5M2vWrOHGjRs4OzsDMGfOHCIiIli0aBFvvvlmWcQtkqLWlJqaCuT/W2BjY0PNmjXL9G9BURS1pvfff589e/YUuKZd8+bNeeqpp1i0aJExYxaZIT93i0qaKSPz8PDAw8OjSOtevnyZ0NBQ/X8wd49NCQkJYerUqcTFxek/tDdu3IiNjU2ZjisoTk0Pkp6ejoWFRb7/nu/cv/OfnbEZsp42bdoAcOrUKapXrw5AUlISCQkJZToGzJA1rVy5Mt9ewv379zNs2DC2b99OrVq1DPIcRWHImiBvj9TDDz/MkCFDmDp1qsG2W1SGrMdU/jbcrag1pqenAxT4m2dhYVFmfweKqqg1BQcHY2Njw6lTp2jbti0A2dnZXLhwweTGgxa1pi+++IL3339ff//KlSuEh4ezdOlSWrZsacyIxWLIz92ikmbKRFy5coWOHTvi6+vLJ598wvXr1/WPValSBYAuXboQGBjIoEGD+Pjjj0lKSuK1115j+PDh+v/mTE1sbCxJSUnExsaSm5urn4+kdu3aODo6EhYWxv/+9z9efPFFXn75ZXQ6HR988AGWlpaEhoaqG74QD6qnbt269O7dmzFjxjBv3jycnZ0ZP3489evXN8l64ME13d0wJSQkABAQEGCy41keVNOxY8cIDQ2lS5cujBs3Tj+uSKvVUrlyZRWTF+5B9ZTHvw3/FRISgpubG0OGDGHChAnY2dnxzTffcP78eXr06KF2vBJxdnZmxIgRTJw4ER8fH/z8/Pj4448BeOyxx1ROVzJ3j5l0dHQEoFatWvp/HsuTonzuFplhTyoUJbVgwQIFKPTrv/7++2+lR48eip2dneLu7q689NJLSkZGhkqpH2zIkCGF1rRlyxb9Ohs3blTatGmjuLi4KG5ubsrDDz+s7N69W73Q91GUepKTk5Vhw4Yprq6uiru7u9K3b998Uz+YmqLU9F9btmwx+akRHlTTxIkTC33cz89P1dz3UpT3qLz9bbjb/v37lS5duiju7u6Kk5OT0qpVK2XdunVqxyqVrKws5dVXX1U8PT0VJycnpXPnzsrRo0fVjmUw58+fL9dTIxT1c7coNIryzwAIIYQQQghRbHI2nxBCCCFEKUgzJYQQQghRCtJMCSGEEEKUgjRTQgghhBClIM2UEEIIIUQpSDMlhBBCCFEK0kwJIYQQQpSCNFNCCCGEEKUgzZQQolwbOnQoffr0UTuGEKICk2ZKCFFAfHw8L7zwAr6+vtjY2FClShXCw8PZvXu3fh2NRsPq1avVC/mPzz//nIULF6odw2xIcypE8cmFjoUQBfTr14/s7GwWLVpEzZo1uXbtGps2bSIpKUntaAW4uLioHUEIUdEZ/MqBQohy7caNGwqgbN269Z7r+Pn53fMCwb/99pvSrFkzxcbGRvH391cmTZqkZGdn6x8HlDlz5ihdu3ZVbG1tlRo1aijLli27b6bly5crQUFBiq2treLu7q506tRJuXXrlqIoeRcB7t27t6Io/1549e6vDh066Le1c+dOpV27doqtra1SvXp15eWXX9Zv617uV9PkyZOVqlWrKgkJCfr1e/bsqbRr107Jzc0tcs2HDx9WQkND9TUOHz5cSU1N1T9+p86PP/5YqVKliuLu7q6MGjVKycrK0q+TmZmp/O9//1O8vb0Ve3t75aGHHsp3MeQFCxYoLi4uyvr165X69esrDg4OSnh4uHLlyhVFUQq/APS9LngthPiXNFNCiHyys7MVR0dHZezYsUpGRkah68THxyuAsmDBAiUuLk6Jj49XFEVR1q9frzg7OysLFy5Uzp49q2zcuFGpUaOGMmnSJP33AkqlSpWUb775Rjl16pTyzjvvKFqtVjl+/Hihz3XlyhXF0tJSmTFjhnL+/Hnl8OHDyuzZs/WNxn+bqZycHCUuLk7/dejQIaVSpUrKu+++qyhKXsPi6OiofPbZZ8rp06eVnTt3Kk2bNlWGDh16z9fjQTXl5OQoISEhSp8+fRRFUZS5c+cqLi4uyoULF4pcc1pamuLt7a08+uijypEjR5RNmzYp/v7+ypAhQ/TbGDJkiOLs7KyMGDFCOXHihPL7778r9vb2yrx58/TrDBw4UGndurUSGRmpxMTEKB9//LFiY2OjnD59WlGUvGbKyspK6dy5s7J//34lKipKCQgIUAYOHKgoiqKkpqYqjz/+uNK1a1f9a5iZmXnP10YIkUeaKSFEAStWrFDc3NwUW1tbpXXr1sr48eOVv/76K986gLJq1ap8y9q1a6dMmzYt37Lvv/9eqVq1ar7vGzFiRL51WrZsqYwcObLQLFFRUQqQrzn5r/82U/91+/ZtpWXLlsojjzyi30M0aNAg5fnnn8+33vbt2xULCwvl9u3bhW6/KDWdPXtWcXJyUt544w3F3t5e+eGHH/Kt/6Ca582bp7i5ueXbQ7Z27VrFwsJCuXr1qr5OPz8/JScnR7/OY489pgwYMEBRFEWJiYlRNBqNcvny5XzP06lTJ2X8+PGKouQ1U4ASExOjf3z27NmKl5eX/v69Xk8hxL3JmCkhRAH9+vWjR48ebN++nd27d7N+/Xo++ugj5s+fz9ChQ+/5fVFRUezfv5+pU6fql+Xm5pKRkUF6ejr29vYAhISE5Pu+kJAQoqOjC91m48aN6dSpEw0bNiQ8PJwuXbrQv39/3Nzc7lvDs88+S2pqKhEREVhYWOjzxcTE8OOPP+rXUxQFnU7H+fPnCQgIKFFNNWvW5JNPPuGFF15gwIABPPXUUwW2c7+aT5w4QePGjXFwcNA/3qZNG3Q6HadOncLLywuABg0aoNVq9etUrVqVI0eOAHDw4EEURaFu3br5niczM5NKlSrp79vb21OrVq1824iPj7/HqyiEKApppoQQhbK1tSUsLIywsDAmTJjAc889x8SJE+/bTOl0OiZPnsyjjz5a6PbuR6PRFLpcq9USERHBrl272LhxI19++SVvv/02e/fuxd/fv9Dvef/991m/fj379u3DyckpX74XXniB0aNHF/geX1/fUtUUGRmJVqvlwoUL5OTkYGn54D+vd2pWFOWe9f93uZWVVYHHdDqdPqdWqyUqKipfwwXg6Oh4320oivLArEKIe5OpEYQQRRIYGEhaWpr+vpWVFbm5ufnWadasGadOnaJ27doFvu7sHQLYs2dPvu/bs2cP9evXv+dzazQa2rRpw+TJkzl06BDW1tasWrWq0HVXrlzJlClTWLZsWb49MHfyHTt2rNB81tbWhW6vKDUtXbqUX375ha1bt3Lx4kXee++9Atu5X82BgYFER0fne3137tyJhYVFgT1N99K0aVNyc3OJj48vkLNKlSpF2gaAtbV1gfdVCHF/smdKCJFPYmIijz32GMOGDaNRo0Y4OTlx4MABPvroI3r37q1fr0aNGmzatIk2bdpgY2ODm5sbEyZM4JFHHsHHx4fHHnsMCwsLDh8+zJEjR3j//ff137t8+XKaN29O27Zt+fHHH9m3bx/ffvttoXn27t3Lpk2b6NKlC56enuzdu5fr168Xekju6NGjDB48mDfeeIMGDRpw9epVIK9BcHd354033qBVq1a8+OKLDB8+HAcHB06cOEFERARffvlloc//oJouXbrEyJEj+fDDD2nbti0LFy6kR48edOvWjVatWhWp5qeeeoqJEycyZMgQJk2axPXr13n55ZcZNGiQ/hDfg9StW5ennnqKwYMH8+mnn9K0aVMSEhLYvHkzDRs2pHv37kXaTo0aNdiwYQOnTp2iUqVKuLi4FNibJYS4i7pDtoQQpiYjI0N58803lWbNmikuLi6Kvb29Uq9ePeWdd95R0tPT9ev99ttvSu3atRVLS8t8UyOsX79ead26tWJnZ6c4OzsrDz30UL4zzgBl9uzZSlhYmGJjY6P4+fkpP/300z3zHD9+XAkPD1cqV66s2NjYKHXr1lW+/PJL/eP/HTB9Z4D13V//nRph3759SlhYmOLo6Kg4ODgojRo1UqZOnXrf1+ReNel0OqVTp05KeHi4otPp9Ou/8sorSq1atfRnHBal5qJOjfBfY8aMyVdbVlaWMmHCBKVGjRqKlZWVUqVKFaVv377K4cOH9a+Pi4tLvm2sWrVK+e9HQXx8vP71QaZGEKJINIoiB8uFEGVHo9GwatWqCjXLdkWsWYiKRMZMCSGEEEKUgjRTQgghhBClIIf5hBBCCCFKQfZMCSGEEEKUgjRTQgghhBClIM2UEEIIIUQpSDMlhBBCCFEK0kwJIYQQQpSCNFNCCCGEEKUgzZQQQgghRClIMyWEEEIIUQr/B+hbZ2kaHKylAAAAAElFTkSuQmCC\n",
                        "text/plain": [
                            "<Figure size 640x480 with 1 Axes>"
                        ]
                    },
                    "metadata": {},
                    "output_type": "display_data"
                }
            ],
            "source": [
                "h_lst = 10.**(-np.arange(3,21))\n",
                "\n",
                "plt.semilogy(np.log10(h_lst), [np.abs(df(x)[0] - (f(x+[h,0,0])-f(x))/h) for h in h_lst], label='Finite difference')\n",
                "plt.semilogy(np.log10(h_lst), [np.abs(df(x)[0] - np.imag(f(x+[h*1j,0,0]))/h) for h in h_lst], label='Complex step')\n",
                "plt.xticks(np.arange(-20,-1,2))\n",
                "setup_plot(ylabel='Error of gradient', xlabel='Step size exponent')"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "b27fdb2f",
            "metadata": {},
            "source": [
                "**Common code changes**\n",
                "\n",
                "The complex step method calls the function with a complex number, i.e. all intermediate functions and routines must support  complex number. A few `numpy` functions have different or undefined behaviour for complex numbers, so often a few changes is required. In PyWake, the module `py_wake.utils.gradients` contains a set of replacement functions that supports complext number, e.g.:\n",
                "\n",
                "- `abs`\n",
                "  - For a real value, `x`, `abs(x)` returns the positive value, while for a complex number, it returns the distance from 0 to z, $abs(a+bi)= \\sqrt{a^2+b^2}$. \n",
                "  - In most cases `abs` should therefore be replaced by `gradients.cabs`, which returns `np.where(x<0,-x,x)`\n",
                "- `np.hypot(a,b)`\n",
                "  - `np.hypot` does not support complex numbers\n",
                "  - replace with `gradients.hypot`, which returns `np.sqrt(a\\*\\*2+b\\*\\*2)` if `a` or `b` is complex\n",
                "- `np.interp(xp,x,y)`\n",
                "  - replace with `gradients.interp(xp,x,y)`\n",
                "- `np.logaddexp(x,y)`\n",
                "  - replace with  `gradients.logaddexp(x,y)` \n",
                "  \n",
                "Furthermore, the imaginary part must be preserved when creating new arrays, i.e.\n",
                "- `np.array(x,dtype=float)` -> `np.array(x,dtype=(float, np.complex128)[np.iscomplexobj(x)])`\n"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "59086a67",
            "metadata": {},
            "source": [
                "### Automatic Differentiation (Autograd)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "76fd609d",
            "metadata": {},
            "source": [
                "[Autograd](https://github.com/HIPS/autograd) is a python package that can automatically differentiate native Python and Numpy code.\n",
                "\n",
                "Autograd performs a two step automatic differentiation process.\n",
                "\n",
                "First the normal result is calculated and during this process autograd setups up a calculation tree where each element in the tree holds the associated gradient functions:\n",
                "\n",
                "<center><img src=\"../_static/autograd_calculation.svg\" width=\"400\"/></center>\n",
                "\n",
                "For most numpy functions, the associated gradient function is predefined when using `autograd.numpy` instead of `numpy`. You can see the autograd module that defines the gradients of numpy functions [here](https://github.com/HIPS/autograd/blob/master/autograd/numpy/numpy_vjps.py#L32) and the functions used in the example is shown here:\n",
                "\n",
                "```python\n",
                "defvjp(anp.multiply,    lambda ans, x, y : unbroadcast_f(x, lambda g: y * g),\n",
                "                        lambda ans, x, y : unbroadcast_f(y, lambda g: x * g))\n",
                "defvjp(anp.add,         lambda ans, x, y : unbroadcast_f(x, lambda g: g),\n",
                "                        lambda ans, x, y : unbroadcast_f(y, lambda g: g))\n",
                "defvjp(anp.power,\n",
                "    lambda ans, x, y : unbroadcast_f(x, lambda g: g * y * x ** anp.where(y, y - 1, 1.)),\n",
                "    lambda ans, x, y : unbroadcast_f(y, lambda g: g * anp.log(replace_zero(x, 1.)) * x ** y))\n",
                "defvjp(anp.sin,    lambda ans, x : lambda g: g * anp.cos(x))\n",
                "```\n",
                "\n",
                "In the second step, the gradients are calculated by backward propagation\n",
                "\n",
                "<center><img src=\"../_static/autograd_differentiation.svg\" width=\"400\"/></center>"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "093a9b84",
            "metadata": {},
            "source": [
                "**Applied to the example function,** `autograd`, **gives the exact results.**"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 8,
            "id": "7873b0aa",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "Analytical gradient: [6.129430520583658, 15.164788859062082, -45.83911438119122]\n",
                        "Autograd gradient: [6.129430520583658, 15.164788859062082, -45.83911438119122]\n"
                    ]
                }
            ],
            "source": [
                "from py_wake import np\n",
                "from py_wake.utils.gradients import autograd\n",
                "\n",
                "def f(x):\n",
                "    return np.sum((2 * x**3) * np.sin(x))\n",
                "\n",
                "print (\"Analytical gradient:\", list(df(x)))\n",
                "print (f\"Autograd gradient:\", list(autograd(f)(x)))"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "d7ce4ab1",
            "metadata": {},
            "source": [
                "Note, autograd needs its own numpy, `autograd.numpy`, to work. In PyWake, the `autograd` wrapper defined in `py_wake.utils.gradients`, handles this numpy replacement automatically. All it requires is to use `from py_wake import np` instead of the standard `import numpy as np`. This approach also allows an easy switch to single precision for faster simulation."
            ]
        },
        {
            "cell_type": "markdown",
            "id": "cc7e8ed0",
            "metadata": {},
            "source": [
                "**Common code changes**\n",
                "\n",
                "- `x[m] = 0` -> `x = np.where(m,0,x)`\n",
                "  - Item assignment not supported\n",
                "  "
            ]
        },
        {
            "cell_type": "markdown",
            "id": "e18c09b5",
            "metadata": {},
            "source": [
                "### Comparison - Scalability of example problem\n",
                "As seen in the examples, autograd computed the gradients with respect to all input elements in one smart (but slow) function evaluation, while finite difference and complex step required `n + 1` and `n` function evaluations, respectively.\n",
                "\n",
                "This difference has a high impact on the performance of large scale problems. The plot below shows the time required to compute the gradients as a function of the number of elements in the input vector. In this example the `fd`, `cs` and `autograd` functions from `py_wake.utils.gradients` is utilized."
            ]
        },
        {
            "cell_type": "markdown",
            "id": "69dd031e",
            "metadata": {},
            "source": [
                "    from py_wake.utils.gradients import fd, cs, autograd\n",
                "    from py_wake.tests.check_speed import timeit\n",
                "\n",
                "    n_lst = np.arange(1,3500,500)\n",
                "    x_lst = [np.random.random(n) for n in n_lst]\n",
                "\n",
                "    def get_gradients(method,x):\n",
                "        return method(f, vector_interdependence=True)(x)\n",
                "\n",
                "    for method in  [fd, cs, autograd]:\n",
                "        plt.plot(n_lst, [np.mean(timeit(get_gradients, min_time=.2)(method,x)[1]) for x in x_lst], label=method.__name__)\n",
                "    setup_plot(title='Time to compute gradients of f(x)', xlabel='Number of elements in x', ylabel='Time [s]')"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "407d2c22",
            "metadata": {},
            "source": [
                "![image1.png](images/Optimization_gradient_methods.png)"
            ]
        },
        {
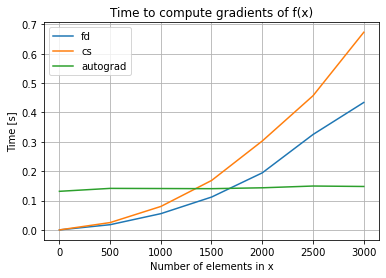            "cell_type": "markdown",
            "id": "d8a0e437",
            "metadata": {},
            "source": [
                "### Gradients in PyWake\n",
                "\n",
                "As described above, PyWake, contains a module, `py_wake.utils.gradients` which defines the three methods, `fd`, `cs` and `autograd`, as well as a number of helper functions and constructs.\n",
                "\n",
                "With only a few exceptions, all PyWake models, turbines and sites support the three gradient methods.\n",
                "\n",
                "Unfortunately, autograd is not working very well with xarray, i.e. the normal xarray `SimulationResult` must be bypassed. This mean that you can compute gradients of the [AEP](#Gradients-of-AEP) or [WS, TI, Power and custom functions](#Gradients-of-WS,-TI,-Power-and-custom-functions) by setting the argument `return_simulationResult=False` when running the wind farm model:  `WindFarmModel(..., return_simulationResult=False)`.\n",
                "\n",
                "Below we show a simple example with the Hornsrev1 Site and turbines while using the ZongGaussian wake model."
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 9,
            "id": "2fcd561f",
            "metadata": {},
            "outputs": [],
            "source": [
                "import numpy as np\n",
                "import matplotlib.pyplot as plt\n",
                "\n",
                "from py_wake.examples.data.hornsrev1 import Hornsrev1Site, HornsrevV80\n",
                "from py_wake.utils.gradients import fd, cs, autograd\n",
                "from py_wake.utils.profiling import timeit\n",
                "from py_wake.utils.plotting import setup_plot\n",
                "from py_wake.deficit_models.gaussian import ZongGaussian, BastankhahGaussian\n",
                "from py_wake.deflection_models.jimenez import JimenezWakeDeflection\n",
                "from py_wake.turbulence_models.crespo import CrespoHernandez\n",
                "from py_wake.utils.layouts import rectangle"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 10,
            "id": "1aa9df78",
            "metadata": {},
            "outputs": [],
            "source": [
                "site = Hornsrev1Site()\n",
                "wt = HornsrevV80()\n",
                "wfm = ZongGaussian(site, wt, deflectionModel=JimenezWakeDeflection(), turbulenceModel=CrespoHernandez())"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 11,
            "id": "05202062",
            "metadata": {},
            "outputs": [
                {
                    "data": {
                        "text/plain": [
                            "<matplotlib.contour.QuadContourSet at 0x2e0eb1df7c0>"
                        ]
                    },
                    "execution_count": 11,
                    "metadata": {},
                    "output_type": "execute_result"
                },
                {
                    "data": {
                        "image/png": "iVBORw0KGgoAAAANSUhEUgAAAjgAAAGdCAYAAAAfTAk2AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAA9hAAAPYQGoP6dpAAB9TklEQVR4nO3dd3wUZeI/8M+WZBNCEkJLCB1EWkCqQFCK0k5APe8EBSmChUNERD3BBoKAICCCiHI/JSJSvh6ieCdSzhNEUJAmoIKn1JAYUcjSkuzOzO+PzUxmdmd7Szaf9+u1L9iZZ8rObnY++zzPPGOQJEkCERERUQwxRnsHiIiIiEKNAYeIiIhiDgMOERERxRwGHCIiIoo5DDhEREQUcxhwiIiIKOYw4BAREVHMYcAhIiKimGOO9g5EgiiKOHfuHJKTk2EwGKK9O0REVI5JkoRLly4hMzMTRmP46gGKiopQUlIS9Hri4+ORkJAQgj2KLZUi4Jw7dw7169eP9m4QEVEFcubMGdSrVy8s6y4qKkKjxo3xa35+0OvKyMjAiRMnGHKcVIqAk5ycDMDxYU1JSYny3hARUXlmtVpRv3595dwRDiUlJfg1Px/HfwnuvGS1WnF9k/ooKSlhwHFSKQKO3CyVkpLCgENERD6JRJcGnpfCh52MiYiIKOZUihocIiKi8kiUJIiSFNTypI81OERERBRzWINDRBQjBEGAzWaL9m6UeyaTCWazmcOGxDgGHCKiGHD58mWcPXsWEpssfFKlShXUqVMH8fHx0d4VChMGHCKiCk4QBJw9exZVqlRBrVq1WDPhgSRJKCkpwW+//YYTJ06gWbNmYR3MzxtRlCCKQfTBCWLZWMeAQ0RUwdlsNkiShFq1aiExMTHau1PuJSYmIi4uDqdOneL4MTGMnYyJiGIEa258F81aG4oMvsNEREQUc9hERUREFCWCJEEIomN4MMvGOtbgEBERUcxhwCEiIsWlS5fwxRdf4NKlS2HdzuDBg9GnTx/debt374bBYMD+/fuxd+9e3HrrrahWrRrS0tLQr18/HDx4UFP+8OHD6NmzJxITE1G3bl3MmDGDl8sTAw4REZW5fPkytm/fjsuXL4d1O2PHjsXnn3+OU6dOucx755130K5dOzRr1gz9+/dHgwYN8M0332Dnzp1ISUlB//79lQENrVYr+vbti8zMTOzduxdLlizB/PnzsXDhwrDuP5V/DDhERBRxgwYNQu3atZGTk6OZfvXqVaxbtw5jx47FsWPHcOHCBcyYMQPNmzdH69atMW3aNBQUFOD06dMAgPfffx9FRUXIyclBVlYW7rrrLjzzzDNYuHBhhajFkaTgH6SPAYeIiBRyKAh3ODCbzRg5ciRycnI02/rggw9QUlKC4cOHo3nz5qhZsybefvttlJSU4Nq1a3j77bfRunVrNGzYEICjOatnz56wWCzKOvr3749z587h5MmTYX0NVL4x4BAREQDgypUr+OyzzwAAn332Ga5cuRLW7Y0ZMwYnT57EF198oUx75513cNdddyEtLQ3Jycn44osvsGrVKiQmJqJq1arYvHkzPv30U5jNjouA8/PzkZ6erlmv/Dw/Pz+s+0/lGwMOERHh6NGjWLp0KX7//Xe0bt0av//+O5YuXYqjR4+GbZstWrRAdnY23nnnHQDAzz//jC+//BJjxowBAFy7dg1jxoxB9+7d8fXXX+Orr75C69atcdttt+HatWvKepwHOJRrhDjwYeXGcXCIiAgFBQVo1KgRBg4ciKSkJFy5cgX//ve/8dtvv4V1u2PHjsWECROwdOlSrFixAg0bNsStt94KAFi9ejVOnjyJ3bt3KyMPr169Gmlpafj4449xzz33ICMjw6WmpqCgAABcanbKI1GUIPBeVGHBGhwiIkKvXr0wZMgQJCUlAQCSkpIwZMgQ9OzZM6zbHTJkCEwmE1avXo13330X999/v1LzcvXqVRiNRk1NjPxcFEUAQLdu3bBjxw6UlJQoZbZs2YLMzEw0atQorPtO5RsDDhERuW3OCXczT9WqVTF06FA888wzOHfuHEaPHq3M69u3Ly5cuIBHHnkEP/zwA44ePYr7778fZrMZvXv3BgAMGzYMFosFo0ePxpEjR7BhwwbMnj0bkydPZhNVJceAQ0REUTV27FhcuHABffr0QYMGDZTpLVq0wCeffILvvvsO3bp1w80334xz587hs88+Q506dQAAqamp2Lp1K86ePYtOnTph/PjxmDx5MiZPnhytl0PlBPvgEBFRVHXr1s3tZel9+/ZF3759PS7fpk0b7NixIxy7RhUYAw4REVGUiJIEMYgxh4JZNtaxiYqIiIhiDgMOERERxRwGHCIiIoo5DDhERDGiItxcsrwoL8dKFIN/+OvSpUuYNGkSGjZsiMTERGRnZ2Pv3r0elykuLsazzz6Lhg0bwmKxoGnTpsoI1LL169ejVatWsFgsaNWqFTZs2OD/zoUQOxkTEVVwJpMJAFBSUoLExMQo703FcPXqVQBAXFxclPck8h544AEcOXIE7733HjIzM7Fq1Sr06dMH33//PerWrau7zJAhQ/Drr7/i7bffxnXXXYeCggLY7XZl/u7duzF06FDMnDkTf/7zn7FhwwYMGTIEO3fuRJcuXSL10jQMUnmJsWFktVqRmpqKwsJCpKSkRHt3iIhCSpIknD59GjabDZmZmcptDciVJEm4evUqCgoKUK1aNWU8HbVInDPkbRw/fR7JQWzjktWK6xvU9Hlfr127huTkZHz88ccYOHCgMr1du3YYNGgQXnrpJZdlPvvsM9xzzz345ZdfUL16dd31Dh06FFarFZs2bVKmDRgwAGlpaVizZk0Aryx4rMEhIqrgDAYD6tSpgxMnTuDUqVPR3p0KoVq1asjIyIj2boSM1WrVPLdYLLBYLC7l7HY7BEFAQkKCZnpiYiJ27typu+6NGzeiU6dOmDdvHt577z0kJSXh9ttvx8yZM5Uaw927d+Pxxx/XLNe/f38sWrQoiFcVHAYcIqIYEB8fj2bNmmnuyUT64uLilGa9aBMkCUIQDSnysvXr19dMnzZtGqZPn+5SPjk5Gd26dcPMmTPRsmVLpKenY82aNfjmm2/QrFkz3W388ssv2LlzJxISErBhwwacP38e48ePxx9//KH0w8nPz3e5uWl6errLjVAjiQGHiChGGI1Gl1/mVDmcOXNG00SlV3sje++99zBmzBjUrVsXJpMJHTp0wLBhw7B//37d8qIowmAw4P3330dqaioAYOHChfjrX/+KpUuXKrU4zvf+kiQpqvcDY0MtERFRBZeSkqJ5eAo4TZs2xfbt23H58mWcOXMGe/bsgc1mQ+PGjXXL16lTB3Xr1lXCDQC0bNkSkiTh7NmzAICMjAyX2pqCggKXWp1IYsAhIiKqhJKSklCnTh1cuHABmzdvxh133KFbrnv37jh37hwuX76sTDt+/DiMRiPq1asHwHE/sa1bt2qW27JlC7Kzs8P3ArxgwCEiIooSUZSCfvhr8+bN+Oyzz3DixAls3boVvXv3RvPmzXH//fcDAKZOnYqRI0cq5YcNG4YaNWrg/vvvx/fff48dO3bgqaeewpgxY5TmqcceewxbtmzB3Llz8eOPP2Lu3LnYtm0bJk2aFJLjFAgGHCIiokqksLAQjzzyCFq0aIGRI0fipptuwpYtW5QxgfLy8nD69GmlfNWqVbF161ZcvHgRnTp1wvDhwzF48GAsXrxYKZOdnY21a9dixYoVaNu2LXJycrBu3bqojYEDcBwcIiIijUiOg3P0REHQ4+C0blyb5zcdrMEhIiKimMPLxImIiKJEQJDj4CDmG2ECxhocIiIiijkMOERERBRzGHCIiIgo5rAPDhERUZSIouMRzPKkjzU4REREFHMYcIiIiCjmRCzgzJkzBwaDQTNssyRJmD59OjIzM5GYmIhevXrh6NGjmuWKi4vx6KOPombNmkhKSsLtt9+u3NyLiIiISE9EAs7evXuxfPlytG3bVjN93rx5WLhwIV5//XXs3bsXGRkZ6Nu3Ly5duqSUmTRpEjZs2IC1a9di586duHz5MgYNGgRBECKx60RERFQBhT3gXL58GcOHD8c//vEPpKWlKdMlScKiRYvw7LPP4q677kJWVhbeffddXL16FatXrwbguF/G22+/jQULFqBPnz5o3749Vq1ahcOHD2Pbtm3h3nUiIqKwkiQp6AfpC3vAeeSRRzBw4ED06dNHM/3EiRPIz89Hv379lGkWiwU9e/bErl27AAD79u2DzWbTlMnMzERWVpZSRk9xcTGsVqvmQURERJVHWC8TX7t2Lfbv34+9e/e6zMvPzwcApKena6anp6fj1KlTSpn4+HhNzY9cRl5ez5w5c/Diiy8Gu/tERERUQYWtBufMmTN47LHHsGrVKiQkJLgtZzAYNM8lSXKZ5sxbmalTp6KwsFB5nDlzxr+dJyIiogotbAFn3759KCgoQMeOHWE2m2E2m7F9+3YsXrwYZrNZqblxrokpKChQ5mVkZKCkpAQXLlxwW0aPxWJBSkqK5kFERFTeiJLjZpuBPkT2wXErbAHn1ltvxeHDh3Hw4EHl0alTJwwfPhwHDx5EkyZNkJGRga1btyrLlJSUYPv27cjOzgYAdOzYEXFxcZoyeXl5OHLkiFKGiIiIyFnY+uAkJycjKytLMy0pKQk1atRQpk+aNAmzZ89Gs2bN0KxZM8yePRtVqlTBsGHDAACpqakYO3YsnnjiCdSoUQPVq1fHk08+iTZt2rh0WiYiIiKSRfVeVH//+99x7do1jB8/HhcuXECXLl2wZcsWJCcnK2VeffVVmM1mDBkyBNeuXcOtt96KnJwcmEymKO45ERERlWcGqRJcRG+1WpGamorCwkL2xyEiIo8icc6Qt7H3WB6qJge+jcuXrOjcvA7Pbzp4LyoiIiKKOQw4REREFHMYcIiIiCjmRLWTMRERUWUmBjmWDcfBcY81OERERBRzGHCIiIgo5jDgEBERUcxhwCEiIooSUZSCfvjr0qVLmDRpEho2bIjExERkZ2dj7969bsvn5eVh2LBhaN68OYxGIyZNmuRSJicnBwaDweVRVFTk9/6FCgMOERFRJfLAAw9g69ateO+993D48GH069cPffr0QW5urm754uJi1KpVC88++yxuuOEGt+tNSUlBXl6e5pGQkBCul+EVAw4REVElce3aNaxfvx7z5s1Djx49cN1112H69Olo3Lgxli1bprtMo0aN8Nprr2HkyJFITU11u26DwYCMjAzNI5oYcIiIiCo4q9WqeRQXF+uWs9vtEATBpWYlMTERO3fuDGofLl++jIYNG6JevXoYNGgQDhw4ENT6gsWAQ0REFCWCJAX9AID69esjNTVVecyZM0d3e8nJyejWrRtmzpyJc+fOQRAErFq1Ct988w3y8vICfh0tWrRATk4ONm7ciDVr1iAhIQHdu3fHTz/9FPA6g8WB/oiIiCq4M2fOaG62abFY3JZ97733MGbMGNStWxcmkwkdOnTAsGHDsH///oC337VrV3Tt2lV53r17d3To0AFLlizB4sWLA15vMFiDQ0REVMGlpKRoHp4CTtOmTbF9+3ZcvnwZZ86cwZ49e2Cz2dC4ceOQ7Y/RaETnzp2jWoPDgENERFQJJSUloU6dOrhw4QI2b96MO+64I2TrliQJBw8eRJ06dUK2Tn+xiYqIiChKRNHxCGZ5f23evBmSJKF58+b43//+h6eeegrNmzfH/fffDwCYOnUqcnNzsXLlSmWZgwcPAnB0JP7tt99w8OBBxMfHo1WrVgCAF198EV27dkWzZs1gtVqxePFiHDx4EEuXLg38xQWJAYeIiKgSKSwsxNSpU3H27FlUr14df/nLXzBr1izExcUBcAzsd/r0ac0y7du3V/6/b98+rF69Gg0bNsTJkycBABcvXsRDDz2E/Px8pKamon379tixYwduvPHGiL0uZwZJiv1bkVqtVqSmpqKwsFDTCYuIiMhZJM4Z8jZ2HD6LqsmBb+PyJSt6tKnH85sO9sEhIiKimMOAQ0RERDGHfXCIiIiiRJQkiEH0FAlm2VjHGhwiIiKKOQw4REREFHMYcIiIiCjmsA8OERFRlLAPTviwBoeIiIhiDgMOERERxRwGHCIiIoo57INDREQUJVKQN9uUglg21rEGh4iIiGIOAw4RERHFHAYcIiIiijnsg0NERBQlHAcnfFiDQ0RERDGHAYeIiIhiDgMOERERxRz2wSEiIooSuyTBLgbej8bOPjhusQaHiIiIYg4DDhEREcUcBhwiIiKKOeyDQ0REFCV2SYI9iBtKsQ+Oe6zBISIiopjDgENEREQxhwGHiIiIYg4DDhERUZTYRSnoh1/bs9vx3HPPoXHjxkhMTESTJk0wY8YMiKL7fkCjR4+GwWBwebRu3VpTbv369WjVqhUsFgtatWqFDRs2BHRMQoUBh4iIqJKYO3cu3nzzTbz++uv44YcfMG/ePLzyyitYsmSJ22Vee+015OXlKY8zZ86gevXquPvuu5Uyu3fvxtChQzFixAgcOnQII0aMwJAhQ/DNN99E4mXpMkhS7HfBtlqtSE1NRWFhIVJSUqK9O0REVI5F4pwhb2PDnl+QVDU54PVcuXwJf76xic/7OmjQIKSnp+Ptt99Wpv3lL39BlSpV8N577/m0zY8++gh33XUXTpw4gYYNGwIAhg4dCqvVik2bNinlBgwYgLS0NKxZs8bPVxUarMEhIiKqJG666Sb85z//wfHjxwEAhw4dws6dO3Hbbbf5vI63334bffr0UcIN4KjB6devn6Zc//79sWvXrtDseAA4Dg4REVEFZ7VaNc8tFgssFotLuaeffhqFhYVo0aIFTCYTBEHArFmzcO+99/q0nby8PGzatAmrV6/WTM/Pz0d6erpmWnp6OvLz8/18JaHDGhwiIqIoEUQp6AcA1K9fH6mpqcpjzpw5uttbt24dVq1ahdWrV2P//v149913MX/+fLz77rs+7W9OTg6qVauGO++802WewWDQPJckyWVaJLEGh4iIqII7c+aMpg+OXu0NADz11FOYMmUK7rnnHgBAmzZtcOrUKcyZMwejRo3yuA1JkvDOO+9gxIgRiI+P18zLyMhwqa0pKChwqdWJJNbgEBERVXApKSmah7uAc/XqVRiN2lO/yWTyeJm4bPv27fjf//6HsWPHuszr1q0btm7dqpm2ZcsWZGdn+/EqQos1OERERJXE4MGDMWvWLDRo0ACtW7fGgQMHsHDhQowZM0YpM3XqVOTm5mLlypWaZd9++2106dIFWVlZLut97LHH0KNHD8ydOxd33HEHPv74Y2zbtg07d+4M+2tyhwGHiIgoSgRJDOpmm4Kfyy5ZsgTPP/88xo8fj4KCAmRmZuLhhx/GCy+8oJTJy8vD6dOnNcsVFhZi/fr1eO2113TXm52djbVr1+K5557D888/j6ZNm2LdunXo0qWL/y8qRDgODhERkUokx8FZt/snVAliHJyrly9haLdmPL/pCGsfnDlz5qBz585ITk5G7dq1ceedd+LYsWOaMpIkYfr06cjMzERiYiJ69eqFo0ePasoUFxfj0UcfRc2aNZGUlITbb78dZ8+eDeeuExERUQUW1oCzfft2PPLII/j666+xdetW2O129OvXD1euXFHKzJs3DwsXLsTrr7+OvXv3IiMjA3379sWlS5eUMpMmTcKGDRuwdu1a7Ny5E5cvX8agQYMgCEI4d5+IiIgqqIg2Uf3222+oXbs2tm/fjh49ekCSJGRmZmLSpEl4+umnAThqa9LT0zF37lw8/PDDKCwsRK1atfDee+9h6NChAIBz586hfv36+PTTT9G/f3+v22UTFRER+SqSTVSrdx0PuolqWPb1PL/piOhl4oWFhQCA6tWrAwBOnDiB/Px8zfDOFosFPXv2VIZ33rdvH2w2m6ZMZmYmsrKy3A4BXVxcDKvVqnkQERFR5RGxq6gkScLkyZNx0003KZeYyYMC6Q3vfOrUKaVMfHw80tLSXMq4GwJ6zpw5ePHFF12mX7MBcbagXwoREcWwazxPxISI1eBMmDAB3333ne5dRQMZ3tlTmalTp6KwsFB5nDlzJvAdJyIiogonIjU4jz76KDZu3IgdO3agXr16yvSMjAwAjlqaOnXqKNPVwztnZGSgpKQEFy5c0NTiFBQUuB0h0d1NxoiIiMoT9f2kAl2e9IW1BkeSJEyYMAEffvghPv/8czRu3Fgzv3HjxsjIyNAM71xSUoLt27cr4aVjx46Ii4vTlMnLy8ORI0eiOgQ0ERERlV9hrcF55JFHsHr1anz88cdITk5W+sykpqYiMTERBoMBkyZNwuzZs9GsWTM0a9YMs2fPRpUqVTBs2DCl7NixY/HEE0+gRo0aqF69Op588km0adMGffr0CefuExERUQUV1oCzbNkyAECvXr0001esWIHRo0cDAP7+97/j2rVrGD9+PC5cuIAuXbpgy5YtSE4uu2zu1VdfhdlsxpAhQ3Dt2jXceuutyMnJgclkCufuExERUQVVqW7VkH+e4wQQEZFnVqsVGTUjMw7Oii9/DHocnPtvbsFxcHREdBwcIiIiokhgwCEiIqKYE7GB/oiIiIgAYPLkyX4v89xzzyl3QvAFAw4REVGU2EURdlEMavmKaNGiRejWrRvi4+N9Kr9z505MmDCBAYeIiIjKtw0bNqB27do+lVVfWe0r9sEhIiKiiFqxYgVSU1N9Lv/WW2+53LfSG9bgEBERUUSNGjXKr/Ly4L/+YA0OERFVSqIkuX1Q5Jw5cwZnz55Vnu/ZsweTJk3C8uXLg1ovAw4REcUkTwGmvIQYQZRgD+IRCzfbHDZsGP773/8CcNx8u2/fvtizZw+eeeYZzJgxI+D1MuAQEVGFVd4DDHl35MgR3HjjjQCA//u//0NWVhZ27dqF1atXIycnJ+D1sg8OERGVWwwqsc9ms8FisQAAtm3bhttvvx0A0KJFC+Tl5QW8XtbgEBFR1FSEZiQKr9atW+PNN9/El19+ia1bt2LAgAEAgHPnzqFGjRoBr5c1OEREFFYVJaiIpf1ZxAj2a7FLEuxBHJ9gli0v5s6diz//+c945ZVXMGrUKNxwww0AgI0bNypNV4FgwCEioqCV5xATycBCvrt8+TKqVq2KXr164fz587BarUhLS1PmP/TQQ6hSpUrA62fAISIir8pjgGFwqdhq1qyJ3r174/bbb8cdd9yBzMxMzfxGjRoFtX72wSEiIgDl64okUZS8PqhiO3bsGG677TasX78ejRs3RufOnTFz5kx89913IVk/Aw4RUSVSHkJMeQgvgiR5fESKXZRgF4J4+Hms7HY7nnvuOTRu3BiJiYlo0qQJZsyYAdHDTTs//PBD9O3bF7Vq1UJKSgq6deuGzZs3a8rk5OTAYDC4PIqKityut2HDhnj00Uexbds2FBQUYPLkyTh69Ch69OiBxo0b47HHHsPnn38OQRD8eo0yBhwiohgTzRATrfDiLbBEK8CUN3PnzsWbb76J119/HT/88APmzZuHV155BUuWLHG7zI4dO9C3b198+umn2LdvH3r37o3BgwfjwIEDmnIpKSnIy8vTPBISEnzar9TUVNx7771Yu3Ytzp8/j7feeguiKOL+++9HrVq18P777/v9WtkHh4ioAopWs1EkVeYgEi67d+/GHXfcgYEDBwJw9HNZs2YNvv32W7fLLFq0SPN89uzZ+Pjjj/HJJ5+gffv2ynSDwYCMjIyg99FsNqNfv37o168flixZggMHDsBut/u/nqD3hIiIwiLSISZSTUOR5u8mK2KuslqtmucWi0UZPE/tpptuwptvvonjx4/j+uuvx6FDh7Bz506XEOOJKIq4dOkSqlevrpl++fJlNGzYEIIgoF27dpg5c6YmAHlSVFSE7777DgUFBZrmMoPBgMGDB/u8b2oMOEREURSpEBPu8BKp4FIRw4cnNkGCWQj8RdlKl61fv75m+rRp0zB9+nSX8k8//TQKCwvRokULmEwmCIKAWbNm4d577/V5mwsWLMCVK1cwZMgQZVqLFi2Qk5ODNm3awGq14rXXXkP37t1x6NAhNGvWzOP6PvvsM4wcORLnz593mWcwGALug8OAQ0QURhU9wIQzuEQrrHi7QWVFvELrzJkzSElJUZ7r1d4AwLp167Bq1SqsXr0arVu3xsGDBzFp0iRkZmZi1KhRXrezZs0aTJ8+HR9//DFq166tTO/atSu6du2qPO/evTs6dOiAJUuWYPHixR7XOWHCBNx999144YUXkJ6e7nUffMWAQ0QUpEh13g2lcASXSASWWLh7djikpKRoAo47Tz31FKZMmYJ77rkHANCmTRucOnUKc+bM8Rpw1q1bh7Fjx+KDDz5Anz59PJY1Go3o3LkzfvrpJ6/7JF9BFcpwAzDgEBF5VdECTKjCS7hedjRDii/vZXkc1DBUrl69CqNRewG1yWTyeJk44Ki5GTNmDNasWaN0UPZEkiQcPHgQbdq08Vr2r3/9K7744gs0bdrUa1l/MOAQUaUX7hNaqMJLKIJLKF9quINKLAcNmRjkZev+HqPBgwdj1qxZaNCgAVq3bo0DBw5g4cKFGDNmjFJm6tSpyM3NxcqVKwE4ws3IkSPx2muvoWvXrsjPzwcAJCYmIjU1FQDw4osvomvXrmjWrBmsVisWL16MgwcPYunSpV736fXXX8fdd9+NL7/8Em3atEFcXJxm/sSJE/16jTIGHCKKeRUhwAQbXkLxEkMZWKIVTrxURERsHeXVkiVL8Pzzz2P8+PEoKChAZmYmHn74YbzwwgtKmby8PJw+fVp5/tZbb8Fut+ORRx7BI488okwfNWoUcnJyAAAXL17EQw89hPz8fKSmpqJ9+/bYsWOHTzfLXL16NTZv3ozExER88cUXMBgMyjyDwRBwwDFIUuxHZKvVitTUVOSfL/SpjZKIKo5YDy/BvLxgA0u4jm15DxCXrFZc36AmCgvDd86Qz0tzPzuEhKTkgNdTdOUSnh5wQ1j3NdwyMjIwceJETJkyxaX5LBiswSGiciuWw0sgiwUTWEJxLCMRTMrD4H7lYR8qk5KSEgwdOjSk4QZgwCGiKAlneKlIwSWQ0BLMsQtVSIl2CAjnpdyRvEzcJkgwhWAcnIps1KhRWLduHZ555pmQrpcBh4jCIhwBJlrBJdyhJZBjFWhQCWUwqYjjxVD5IwgC5s2bh82bN6Nt27YunYwXLlwY0HoZcIgoYKEMMcGeLMMdXPwJLf4eF3/DSqAhJRyBJNo1OeEgIPZeU3l2+PBh5ZYOR44c0cxTdzj2FwMOEXkUmr4bga2jIoYWf8KKP68vksfQF+W9o3AwYvm1lUf//e9/w7JeBhwiUgTXt8P3Zf096YYjtIQysPj6esJ5jMq2EdBiXlWCC24VkXyt7IMTPgw4RJWcP6HG1xO0rydnX4qFMrCEKqz4chz8q53xuagiHCfhWGxuCkRlGGAw2u666y7k5OT4fGn78OHD8eqrr2ruf+UNA04lFO0/XmMQbaoUOcGexL19zLze8NDLCkIRVry9Rt/Cjvf9APwPJKEIG2xqCQyPW/h9/PHH+O2333wqK0kSPvnkE8ycOZMBh8q3cAcsBqhAOrkGfqJ3N8tdgPG0b55OLJ72Idig4u2E5ks48b2ZyqdirsuxViFieKzDT5IkXH/99WHdBgMOuQi0M6PRWD6CBb+c/OP8frs7UetN1gsxesff3Und3bbcfQY9hxy3szwGlGDDDxD6QOmPytisZArzjxhe/h5+gXQsrlu3rl/lGXAqoXD98YbzS6G8hKdYpHeC9CXMOJ/UnYOA3np9CVPuAoW7kBJo6PHeBBbafjbe9od8JwZ5Gbe3AXMjGRptogRTEN+dtgoaxnr27Bn2bTDgVFLl5Vefr7/EovGLKpZDlfp4+htmPAUZTwHGeTm9wOJr4HEXTjx9TgINQt62Gary5J9gmqJFwfN8O69MigkMOJWQ+oven+/gzZv+heen/h2iKGLi5KcwcvTYgPdB/m4KR9AKVfV1Zamm9jXMOAeZB0cMwe6vdiC7Ry8sW7HGpbw6wDi/z+pyrjVBgQcfvfX5Os/TOgNZV3nnLiAE+rp+zTuLGU+Ow4Xfz8NkNuH+R57CLX+6M4g9dHC7n2EcjK+iv7fkwIBTCan/dn29BNdut+PZp5/CR59uRXJyCm65+UbcNuhOpFWvHtS+mEJQS+L8/Vdeaqf0hLvvgL8ESfIaaNSBo2waMOKB8fjLvSOxft0qCIKkW1sjuqnd8VSz4xJ4QhRu7D581u1S4G1IvqzfH+YQ1iCaDXptMqHdX8lgwoRnZqNxi9a48PtvePiuW9D+pluQWCUpJOvXfw2hoz7eAmtwYgIDTiUkhxp/Bjrbu2cPrm/RErXSMwEAt/QZgG1bN+PPf73Hpbw/N4QVnb5Igql2DkVY8ibYfFIew5co6jczqcMM4Foj0zn7Zny9cwckCSi2ix6XBco+b56au9Tz9AKDXgBxFyx8Du9BhJpwKnZqRvH3BK/+e7DDc5uM+uQeaFCrWqMWEtNqotguokpqDVRNqYbff/8DteITA1qfs2J4fp+C/vtXHaLiCHaWsgvBDdZn99LcVpkx4FRC7tqXPZ18z+WdQ3qdTKVMRmYmzp3L1V1G8PEPTq82w121sy+hKZRhyZ1IhKhIswmOL3N3gcZ5uihJSpApEUSIooRim6jM0/zrVJMjnzzVoUJ9QnUOJc7hw91n1FuYsZfDYKlm9uGzWlJ6gvflM2gyGDye+JzDkvr4+Rv49N6T/x09CFEUkZKegWIPHV58DaE+/d35uNu+1KJetdl9WxmVaww4lZBe04PzPGd2QYAoSWUnQ1GC0WhQngdC9PJFY9RUGbsv5+4LK5iw5E4kQlSkyb8e9QKNqPqs6E23CyIEUUKJXdSEGPkkKYcXQSfYyOvTnlzVNTi+19b4GmBC3XnUbPL//fclzHhsnhIAs4cPsdlgcHuzSDkoCJL2D0r9N1Tiw9+0p+N96eIfWPjMRDz4/Dxc8SMouHtvzUYDvFRAeeXpeLmUNRh8OgYUnPbt2/t8I839+/cHtA0GnEpIHUp8ubIFAGqnZyLv3DmUlDZF5OaexQ0dOivP3fH0a0n+Enb7IRckr2HEZDB47WzofDWUtxomf/rJeNp2MEEqkuQg4S3QiE7P7aKEErujnLXEBsARVuQQI0iSKthImm3ZnaYD2vDhXGWvF7zL0z144rwEHU+fKU/LugtQZg9hwDlSqE/u6mOsDlrqQFTk5g/El3BpKynGgsfH4k+jxiOzZXtcLnH/xxbs++ftmKuZTb4FFvmYXGMNTtjdeeedyv+LiorwxhtvoFWrVujWrRsA4Ouvv8bRo0cxfvz4gLfBgFMJqTvQ+drZs3mbDjj+w/fIPZuLqsnJ2L5tCx6a+DRKbNqFnMOE3V0tiuYLv6yMSyhQrV7vJCFA8vorwOjDr3v1un25OsOXS8h9aaorD52O7YLkNtCom5jkmhm7WBZcrthtsIkiLpXYNCFGHWDkk6p8QpO3Y3OaDmjH9NA7AfpaA+NtbJC4AJoaPdXWeDrZ6m1LXb7Irj8dAGDX/4zobc9sMrgcH7PBALtTE5FcO2TXTCv7wytyqr3QO+Z6AVSSJKx8cTKatu+Klr1uxyWnTkSRCqTego+n+fKxvuYhmIWaXQzuZpuh7tweKdOmTVP+/8ADD2DixImYOXOmS5kzZ84EvA0GnBhmt9tRUlyMKknaqxjkLxr/rnAx4vFnZ2H03X+CKIoY9fAkJCanKZ1LnXlrunFXu6H3ZW5UvpBVQcjXgAQoIclTmBB9PN/J6/fnKguP2/XjSpZwjctz8WIhtn7wD3S+9U7UqttIU0OjDjR2SdQ0K734t3tx4ofDKL52FQ/064Bxc95C3eZtHfMlCTZBKgsxYtn/7appgPbEp2mucldjEILmA7PJe/Wau2Yivf4geidNOdhc02y3tJzNzXI210DkXCbOZIBgLzs28udLfRzlZeS/GXU4k4+/ugbHLgqArQgntqxGYuMbkNS0nUutmXNAcQ6mp458iwOf/xu1GzfHge1bAACDnpiH2o2aa5cL0wnZU2h1F07dvW9Fzj28Kaw++OADfPvtty7T77vvPnTq1AnvvPNOQOtlwIlRoihi4bxZMJlMeOLp5zTz7IIY0FUu3XoPQJde/ZXn3pqn1NwFHr1A4lxWb1m95UwG17Z6o+ZKEncBCfAakmSi77Uucs2SfyHG/bxQhSrNOiUJZ375EQBw9coVFNlE3VDj+L8EuyiiSBBhFyQ89EqOEmQAxwnvj2t22ARHrY061AiiVFarIzg1U6kCi7q2QK8PTqi465OhdyLUC0PO4ce5jNloQJHquRKKnILNNZ1AY3MONKr0HWc0uAQZG1yDjRyAnMOP+oRuh6QNPqXNMrbLFzW1L+5q1ZyDatp17TFxw/eO7auWuXBN29zjLqB6q4nwdtm8u9Cqt5xzSHUOOsXXGHAiKTExETt37kSzZs0003fu3ImEhISA18uAE6OMpV/ggiBAkrTNODZBculTAfh+pYss2CsgXE4SBteThJpL8HH6PtMNQv6EI5mgLuu6vOegpOa9D5Hz9n29Ag3w0HcJ/oWq3NKAk1SnEa7Y7CgWBU2gscv/FyQU2UWlZkYOMOowIwcZuyAq/wKOk6EcWARBG2zksO3cFBJsTY3bE55OiHEOhM7LmpyWUQcks8kA2ATd5dSfYfU8QRVaiqD9G3EONEqNi0kn3JT+DcohySZImpO1Ddrngl1yG37lv+cSQYJkK3vfANfaNqVvlZvQqpnmIbQGOt6M8/sh0wuuzu+3p/dInl/CGpyImjRpEv72t79h37596Nq1KwBHH5x33nkHL7zwQsDrZcCJYTd2zcaer3fhwL696NDpRmW6L1e8eLvaBfDv0lu9K0ecg4/LSUYVeJzLak4cQQYjvTLKNJ0vYH+a1+Sw5K15yQ7J5yuylO37ePw9dvSWJFy68BsA4JpkgN1mU0KNHGbkWpqrNtEl0BTbRU2YkYOMIEiamkK7UBZ2BEGCoAovgqANPpr98yHkmDw0NzmfCJ3Luj7XDyTqk6TJYEAxygJNsU21rBx0nAMQtB2DnYOP/LdnNhqUvzOTqrZGL8zYhbIaGHWwsYmSplbIOfTApHrBqvO4fPwFyXHZv16Y0at9kwOMOsA6h1d5f8v+73/QcRtqnAOL83tu0H9Pndepfs9E+U2NAJsowVgJ70WlNmXKFDRp0gSvvfYaVq9eDQBo2bIlcnJyMGTIkIDXy4ATw27ueQv2fL0L27Zs0gScq3ZHlbG6GQJwverF+YoXebry/wB/fbn8olJ/AbkEGaNuOXXg0XyBOYUddblga4yA0nDhdM6Vyzl3qNYs73x5uYeaHa/NS4Jv/XGMPjSRqZsjL9vssEsSrpWIuqHmqk1UamiKbIIm0BSXCBBKa3nsgqiEGEEn1IiipO3orm6i8qPZU81sdj2gnsKL+vipy6nLyNNNJiOKdeabTUYU28Wyz7OqQ7BgUtdalAYc9RVMcugxGZVOwGZj2dg1cuiRP5OCKCmfZU9hxm8m10miKOFyaQ2GHF6V/6vCjHOQUeaVvv+AOry6hlhfwqvb3fZSw6Z9T/XfX08B1natJOB9o8AMGTIkqDCjhwEnhplMZd9eJSUliI+PhyiV/urW6VsBQNMcAUD5BS//X+buyhdPvF1NEmfSDy1xmi+l0hODm1DkSyByXr+nUOS8fr3yem38jnDhIdSIzmXL+NQE5uMl9N4oTQZGEy4W2ZXmp6s20W2oKbIJyslNrsFRBxr5/3KQEQQRdrvrSU9UTnquzQGSm8+UwV3HX9Vn3eimlkZzcjO7ngBNJgNspT/cHQFIKJ0n6AYfOcTYdU6a8t+MPOCe2WRUXqfJZIBddHxW7YKgfKblcg6izrTAONf+aGqFVP8XVTW18nvt2AfPtXLq8Co4PVeHWXmac4j1q2+Z848jnffRuZxemHUXZGVSBK+iIoeLFy/in//8J3755Rc8+eSTqF69Ovbv34/09HTUrVs3oHUy4MS4QXfchX99/CE+3/YZBtx2OwBHDY5e/wrnMCP3s5CfO7fHy9PV3PXL8XblSZzRNcS4K6MXioILRGVfZr7UEjnK+ReK9JYpK+eh5seHS+jdhSBfmr3++C3fsR+1G6GwSIBNkHCttNZGDi+Ok52E4tKTnjy9pETQnNBsNlETZgRBhCiIyoldEiWXUCM6/Yp3fq45LjoneqPmpKYfcuRQJM83mowoKZHDhjbAyCdM+WSn3HpCUJ8QS8NL6dgq6hOkIDjWJQcTuSOvYBdUn6Gy/nHqsFN6BDRl3E8r3RenTseA+3473oKOPIilXZRQVCK4hBpvtXPOgVY9D4DmswC4hli9917vPXcOuXrvu17YcX5v9UKQPE+yRa6JioDvvvsOffr0QWpqKk6ePIkHHngA1atXx4YNG3Dq1CmsXLkyoPUy4MS4Vq3b4F8ff4jvDh5QAk6RIPjccRSApvMo4PkqGJnLeBxerk5x1xlTnq7phFm6Ljnw6AWiOL3yOjVEemEI8KWGSHAp50+fIqW88/2GPNUWCe7KOY61fpgpneemEuDMz6VXUKU2QEmR4LiKyqm2Rm5+Kipx1NyUlNghCBJspTU5giCiuFjQBBo5zAiCoJy41Cc4T7U3nqhPZoB+wFFPKzvhmSDYBMdzW9lJUixdRpBrXgRteNE7KYqiAKPRAEGQpzt//t2EFXnXS1+7o1ZH0i+LsjJyU5VdcJ3m3F/HOcT40k/HuY+OJJWFWb1gIwdbvRo6b6FW/VlQ8/Y58PS+q99j53l64dbxXBtynN9nRHCgP5sgwRhgc7+8vD8aNWqEU6dOuUwfP348li5dqrvM+++/j3nz5uGnn35CamoqBgwYgPnz56NGjRpKmfXr1+P555/Hzz//jKZNm2LWrFn485//7NM+TZ48GaNHj8a8efOQnJysTP/Tn/6EYcOG+fX61BhwKoGqVZNx+fIlXLx4ASmp1VAkiJp+FuomCU9Xwzi3vwPacOPvjSTddf7T6/in7rPgmO66rHMY0qv9MeuEHU81Q+r9dEyTO5fqhyGXfdM0mWm/1PUCkfriDbPB6HKDQWUZua+GuyvUnGuLBP2y5044Ao41vgbsxYLbYCOf1EpKBIiihJISAXZ76XNVqLGV2CCqTnLqk5v8i10SSk8egp8nEZMZouqXtcFk1oQVG2w6JzLHc7E0sKinG01G2EU7DEZDaW2KCaIgwmgy+hBeZCJcA41zWd+CjqM2RyxtupJKB+4TXfrj6E2T++johRhfQ07ZbkkotgtKsHGuqZODTXGx3SXUOAdbvXCjDj8yycNnwWDSnqbUNTju3m/5ubvpesFHXZsnRLCTcaTt3btXEyiPHDmCvn374u6779Ytv3PnTowcORKvvvoqBg8ejNzcXIwbNw4PPPAANmzYAADYvXs3hg4dipkzZ+LPf/4zNmzYgCFDhmDnzp3o0qWLT/v01ltvuUyvW7cu8vPzA3ylFSjgvPHGG3jllVeQl5eH1q1bY9GiRbj55pujvVsVwl1D7sXKd5Zj44Z/4r7RD+BaiVhWayM6OpX6c1WM8xUxjn9dr4rxxNPVLCanMOP4v7Ypyuz8CyyCQUg93Xu/ISGgMOQoqxNunEZ2dg5EsmK9GzPqhCJbsWMYusslZc1RguA4walrbNwFG7vNrpzQ7CV25UQmn+w0YUYoPWkIqpOHt5DjdHKDKU75V163VFrGYDK7DSx65DJGuclIVUXmCDn64cWkCiSOJixRM00Q5Ofa6XIw8ZWnkBNOogTlvZebouT3X6/GTv0ZcA63LsFW+TzofBbckICy9x2ApPq/qHrvAU81NmXP9Wr1DIIBttJpNgAIsLN7RVCrVi3N85dffhlNmzZFz549dct//fXXaNSoESZOnAgAaNy4MR5++GHMmzdPKbNo0SL07dsXU6dOBQBMnToV27dvx6JFi7BmzRqv+5SQkACr1eoy/dixYy77648KEXDWrVuHSZMm4Y033kD37t3x1ltv4U9/+hO+//57NGjQINq7V+5lZNQBAOTnncPpUydw9fIVCHFVXDqSFtkEJdioO5K6a3937kwIeL/UV++SXl87BDp3BnQOQv6GIM2yRv1g5G/TmHq+/x2oy46TbhBSAopzEHKU1b3btM4ozsVCae3Q1cvKtKISQdPHplhVYyM3Rcm/2G2lQUawCZ6DjRxqlJOZ08kNAOweTnDmuLKy8klNsDtCj2DTnPQAdW8lx9eagLKQo2Y0GVU1NYIyTRKlsqYrZb7o8TJ0X+gFdl94Cusu29Dr4+ZHv7c4kwFi6aE2C8Uw266hRIrXNEfJ4Vb9GXBXa2e32V3DrWDz/zMAOD4H6vGglZBrVp5Lmn8dNX3qGj69Gjy9aUoY87ZP5ZBzQLBYLLBYLB6XKSkpwapVqzB58mS342plZ2fj2Wefxaeffoo//elPKCgowD//+U8MHDhQKbN79248/vjjmuX69++PRYsW+bTvd9xxB2bMmIH/+7//A+AY4+v06dOYMmUK/vKXv/i0Dj0VIuAsXLgQY8eOxQMPPADAkRY3b96MZcuWYc6cOVHeu4qhZq3aOP9bAf5v9XsAALFJF9hrNMFVm+i2M6m634W3K2QA/docwLfOg24v5XTTMdC5U2C4QpC7AKSe5ktNkLv5/oYgxzqDC0IAkH/ye+Qe/BKAIxgk/PELrIn1vNba2EpsLic1W4nNfbBxPqHJJw7RS98bo0n/xGeKcw05OmFHj3M/Dudp6qYPdV8N534ajunaz6F6mt5VOaH6/OlN8xTC1evyVhtpLzgJAKhmv4Bul77E0bjmOCGmuw03csCVPwMuAbekNJTInwPB5vr++9JMaSvW1uQZ5SQmB53SdZi0YVgyxQEmMyShrDnMIBg0NXvOtXxKzZ8tcldRiaLk86Cp7pYHgPr162umT5s2DdOnT/e47EcffYSLFy9i9OjRbstkZ2fj/fffx9ChQ1FUVAS73Y7bb78dS5YsUcrk5+cjPT1ds1x6errPzUvz58/Hbbfdhtq1a+PatWvo2bMn8vPz0a1bN8yaNcundegp9wGnpKQE+/btw5QpUzTT+/Xrh127dukuU1xcjOLiYuW5XtVXZXLJasXv53/TTDP8sgf2pHQIhgRVk5TnK2XUnUrVnQoBbQdS+cvE0xUxenzpHOiY5r6DYHkOQEBwJyDl//L3uZcrx5Q+Hk4dpm3XrpSGm9IvfQANCw8j35CGEnuc2742AYUbf4MN4Ag3yg6rgovOL3fnaQaTWfPZ8dZEoe6T4dofw/G+64Vsvc+XP5+tUNQuAsGFa/V0segKSn7Zr0w3AGhlO4Y8YzVcEhzHuOyHjuP9VjdJacJNSZHrZ0D9/uvV4gCuYUcdatQhVg64JUJZEDa7Cbql09S1e4Jzz34dop+d38uDM2fOICUlRXnurfYGAN5++2386U9/QmZmptsy33//PSZOnIgXXngB/fv3R15eHp566imMGzcOb7/9tlLOuQbIeQR9T1JSUrBz5058/vnn2L9/P0RRRIcOHdCnTx+flnen3Aec8+fPQxAEv9LhnDlz8OKLL0Zi9yqEP/74HZJTB2ADJIhXL8GeaFF1JhZVTVLq5ijfrpgBXC//9XS1hN4var2rI9RlPXUSdDz3fHWEu5OT9nl4wo+7aV5PUur7F9m08+Xp8h2pfQlA9ksX4XxpugFAXNFlCIZUt/1t1O+z8yW/bsk1LOY4x4nI6Pqeu/AWapym6/W/0Asx8i92+f/uO5qGPtiEstkUCF2wkf9vKy5rrpQZASThGi7Bc+2Y5tJvTzUy6nDrSz8s9XS5xg7Q1uKJOiFHXd4pFDn2z6z00wLg0lRZUaWkpGgCjjenTp3Ctm3b8OGHH3osN2fOHHTv3h1PPfUUAKBt27ZISkrCzTffjJdeegl16tRBRkaGy/m4oKDA5bztzS233ILs7GxYLBafw5En5T7gyPxJh1OnTsXkyZOV51ar1aX6rjKpXr0GDAaDJuRIMECwVNUtb1c1NalDji+XA7sLOnonQxtcmyDcjWXi7RJg9XP9E5334ANoa35CHXzUZfVOYsWl3+fyjRpNRm24Ud+Y8ZpqXbCpTlg2/RNZkV31a92cBEekUX8egEuwqJoZnf/18Retc6dgzTz5ZGPTn663Dp1AA2g7lep1KHUXavSW0fts+BqIIxmGfa0JVM93LuOuSTQuyfXEKAEoMlWBSTIAMMJx6bwRosmk9G9yvKbSS+0FAQaT2f242XY4AolLzYwPpyH1Z0QuL4dls/5nxLmGz9cgrH5NsWzFihWoXbu2pi+NnqtXr8Js1r5H8vGRzyndunXD1q1bNf1wtmzZguzsbJ/2RRRFzJo1C2+++SZ+/fVXHD9+HE2aNMHzzz+PRo0aYezYsf68NEW5Dzg1a9aEyWTyKx360rmqMklOSUH/Pw3C5k3/Uj6QUpMbYU5MgtkmKkPEm41GCCaptAbHsazjqhD99eqFG3Ww8fdyUABlnQMBt5cAA9qTmR123ctClXFP4F+Nj8lkhM0mhqW5q9hWWs4maE9yTjdrdP71Xmx3Cj6lx0fpP6EaiE59N2rNjRvlMsZEWJp3QfGxrwE4TmQ/WFqi2JDgeC91+gOYSk9qRjh+7br80jUBgtHgaKIASn9Buwk0SHRZf9l6XE9kvlwho/f+ewu8/jZxRqOGTy/UAMHV1sg04zQlJCH5+k64dPxbAGWfCZsxEUb5VhJmIwBRGTNI+buOB1Di+FcURAhGg8sF8zCZy2rz5Jo8l7Cj893gHH58CTVO0wOp4dMbVDGWiKKIFStWYNSoUS7hZerUqcjNzVUG1xs8eDAefPBBLFu2TGmimjRpEm688Ualaeuxxx5Djx49MHfuXNxxxx34+OOPsW3bNuzcudOn/XnppZfw7rvvYt68eXjwwQeV6W3atMGrr74auwEnPj4eHTt2xNatWzWDBm3duhV33HFHFPesYmnbrgMaN7kOy15/FQBgqt0QcYIBNqOjP0ACgCIIsIsGmATHNEEZsVUqPempfsUJIgxGg3KJLeD4cjOZTNoq6wDGPlHKlnYQdF6XunrZ+UoIx/76EHpKw5N8aah2oDf9kW3l0GOzuR/K32QyoqR0ejG0J0HlvkWl9ywqhqANPYDr/YpsgscToXxXanXwUYcat8GnZlOgNODsTr4Zl+xm3SvgHPtVdmwFCIiLj1MCrFEwlv3fZFROcI6NxJW+ZwmO98/Ne+9unJNAxjjx1uwERD/QOOZ5b34CQl9T4zz4pHqesU5jXDr+LQrj0vBT8g24iniYSgTEx6sHQJT/Tkr/NZaFXfmzYBRKa3kEAZKY4NQ3ywzEJ2q/B3y4VNyxcZ1aHB9q+Bz77V9/LFEKvnnEV/Ygb7ZpD2DZbdu24fTp0xgzZozLvLy8PJw+fVp5Pnr0aFy6dAmvv/46nnjiCVSrVg233HIL5s6dq5TJzs7G2rVr8dxzz+H5559H06ZNsW7dOp/GwAGAlStXYvny5bj11lsxbtw4ZXrbtm3x448/+v36ZOU+4ACOUQ5HjBiBTp06oVu3bli+fDlOnz6tORDkXXJKCgbefhf+vfFDmE7uQ2LTrpr5ZlEqPRWVKS4B4uMd/zcaRQBmFBfbgXgzjIIRthJbWciJ1+lzo3Toc3zUNH+K3sKO03x5WUko+wJzHvcEUF/iqx0LxXk6BJQN9lYaBPwd2dZ5KH93w/g737fI5Z5FpcuXhUqDMhSHHHrc3aCxbJp8L6GyX//uhum3X7sCCwB7cjqKjQml+yuP+6I3qq425JiMprJAIwgww+zS78q5WUsUtF83ev0d9Grp/B+szf8wo32u6ofjJsw4ppX/QOO8z65X5Kmel65PMifAYKmCBElyBPDSCw0Ax3eAyRSHkpLSAfEEM2wljr9BdzW6omBWwg7gNB4OEFzAQeA1fOrnzs2WouT9qryKrF+/fi79MmU5OTku0x599FE8+uijHtf517/+FX/9618D2p/c3Fxcd911LtNFUYQtiNtmVIiAM3ToUPz++++YMWMG8vLykJWVhU8//RQNGzaM9q5VOC1bZ+HfGz+EPf9nVG2hbR81Gw0oUl0eaTYZYTYZUFR6356yk3hcaQdUx69cW4ld+SXn/MveWPpLT55uMMaVVW0rnf6CI49fUnYzQ5MmzHiiG3aM7ke2Ve4fZBdhNqunywO/aYfxl8uXDfrmtB6dexYBZYHHrC6rukGjY55qeac7UqsDjzykv/pu1FV+d/xCK67WALCWHY+yGpuykCMPWme3GyAIRsTBrPTDQhw0g7mpA64/t2Hw5z5SjueR61OlnhdImFFP89bkpF6npzK+Bhrn+c63TNEMM2AoO2aWeJPjM20Qle8A+XNQUuL4jCsjGpcGHd/75sU7PS9rsnS+P5XezVXdNVWrn3ua50sfPedaRQqv1q1b48svv3Q5p3/wwQdo3759wOutMO/i+PHjMX78+GjvRkwwJ1SBvegq4kquoEp8EuKMBphNBlyzlQ0dbzYZS7/UDMplrXbVCK3yF5z6l5y3L7g4xLl0Pkac2eVE6O5O0oBvd5MG9Dsoq+mOfVE6TR2Y9AaK8z40P5zm65d3F3YcOy0X0t5VWi6rXq/6jtTKNFFQ1RLI08pGwjX+fhIAUJRSF6YrV5323VFjYzI5frGLogSTyaS89wBgtxsAOE6CcuAB9IcG0As63q6g83QH8FCPiQR4b2ZSl49mmHF+7inMOK8fgMu4Ser9leTXYjSgakKcZsBPk8GgDPgZH2/SDB8RF2f0el8q5wDs7marMk8jUAd6g1XHc9+CsVBUorttCo9p06ZhxIgRyM3NhSiK+PDDD3Hs2DGsXLkS//rXvwJeb4UJOBQ6jboOwP+++BBXjmxHjW6DUWQXEWcyOB5GR1OG2Whw1AaIEsxGI8yl4+M4B524OJPO+DiuYQfQv9miHHwA/37xu+Mp6Dg/9/bl6Gk9amW1Odqh+UVRKq3N0Q86zsP5q+cpZUt30WQou9mifmDyb1rctQsAAJshrvTkLPefkjRBRhAMyr4ZjaJyMosv/YUvUw/uaHcZ5l6/ul89cB5QdpJx/F/VN8QpwKjnuwsxgPe+Muryvlyu7bysr5dtO6/XU7lQhhnANdDo3uW+9LVLqmCWEGeC3Vj2w8b5li0J8SbN6ObyDVgBx2fBl4FAA6nt8/xDRud9NbvO9/TZkufZI3hqtAsijH6OGea8fEU3ePBgrFu3DrNnz4bBYMALL7yADh064JNPPkHfvn0DXi8DTiWUWqM2AKDE+juqxptKmzocN+GrEmfEVZuIOKMBCXFGFNlEJMSZNDdhFAQJxfHeb8YXyICA7r7ovA0a6CmAeAs9zoHG/aXq/n+BeuJ8zyK1sjBZ2nQl99UxlN2bqKx/kPYmjYDcfFV2DyNAbr5yPY5mVUdiswmlAbYs7Mj76qixUb9X+gHHH673JDPozvMlwAC+hRj1Mr7WxgDB1cg4l/MUZNSvw918f2pmtNNc/07kZSX52BkNqGoxwSYY3d501/n+dJZ4x9+M8+1cAGj//nVu6RLIZ8fT5wbwHIpdp+v83Zp4FW6k9e/fH/379w/pOhlwKhmjwYCkODPS6jTEhbxTEC/ko2qNTNhNom7QSYwz4ppNhMXsuAooIc4Eu+i4hYP8JacOO+5u6wBov+jk4OOYXvYF52lgwFDw1jTiKOP+yzMUtQ6u092fvDXb8jLwlRxyANcbNTrmlzZRyUMFlIYlk8EAk7ksRJlNJmUdyrqVq7HkMU8833PME2/3I9O7ySqg3ydGvaxegFGX9acmBgi+NsZ5nt7zUNTKAP6HGc0+lC4rGMpqcFISTLAJjiYpx414S4Ouh8ADQBN6AAR0Y173V/O50v8s6f/NOf9Nefps2QxsooqGb7/9Fj/88AMMBgNatmyJjh07BrU+BpxKqIrZjNbd+mHnh//AL19tQoe7HoIgGZFgklAkCEgwG1FkF5FgNkKQJFwtvdu4+q7jVS1mzc05Pd11PJhfdK7NHfpfgP7wVMPiHGAc5X37tehc1rmcXqhxLheuk7taXJGjeepaakNNGecvA5PqbuaW0uMiuLnyAtAGIjW9k3TZNpxP6G6Oiw+vL5gAA0QvxOhtDwh9kAGge1NOeR/l/YwzGWCJMwJxjg7p8t88AI+BB4D2/07BxzFNFW50PkvuPkOa1+Yu7Hj4LAGuf48u92pTzRcN8V73g0Ln7NmzuPfee/HVV1+hWrVqAICLFy8iOzsba9asCXigXgacSshsMiClahIAQJJEVDGbIEiOL6t4kxElgogEs+PLqUhwBB2bIEFIKAs7jl93JthECUU2MWS/6vxpAtEbkC5YRjcnAMB7zYNeGY+1QX78onS7Dh+DjfrEWPXSWQBAUbUGMJuMsMTpj9rqe1Ob432wOH2beAySeidll9oL7+HFeV40AgwQnRDjbnnAc5Bxx2QwKmWSLY4anASzI4jIAUcOPPL/5UCinibfOFJuGlWHH5lzU6kvwUaPu7CjF+x1j6ubz1IJIleDE41xcMqbMWPGwGaz4YcffkDz5s0BAMeOHcOYMWMwduxYbNmyJaD1MuBUQpbSwHJdmxvxv8N7UPzHr6hWu64jnEgiLCYJxYKg1OrYJUdYsYsSEsyi40us9EtP/QvPrvp/oL/s1CFI5vxlGEzzSDD0Ak7ZPO9fno5pnn/d+xpm9NblLhA4z0u4eBoAICbXhtlgQEK8u2HpTb51YHQzZIje63e3f3rlncuEIrw4l9WdH+YAA4Q3xACeg4zZoL8duTHYZAQSzEYkmAG709+jHHScQw+gDTnqZfTmKdv0cHJ2PnHrHTM9no6L3vvm/HkAgGIh9m/VUJ58+eWX2LVrlxJuAKB58+ZYsmQJunfvHvB6GXAqIbPJCKNRQptO3dG83Y0wmeIhShLMkgRRNEKUJCSYTLBLjlAjlAYfdc2OIwyVhprSwANAN/QA0AQfwP2vO3UIkslhCHANN3onYE/NKNplPZfz1LSix91Jxd2JXjcUeQkxeuvzFGb05pfUbArL7z8r/ZES3NTgAAA8zfORuxOT3onIWxjxN7zolglhgAF8r4VxTPcvxACB1cY41ukhkOsdpzjH6aBqWm0kmEv7Ycl/eyaU/sApCz2AfvCROQcgoCzoqDmHnlDQe/80890cU+XebWDAiaQGDRroDuhnt9tRt27dgNfLgFMJxZkMECTAaDDDXPpFJoqOkCKKcAk76podOewIkiqsSK6hB4Cmpkd+7u5XnvN05yDkKOtUrS16Dzu+VH2rA1Qg3J20XMp5arJxE4J8qelwV85dgBDqtcXVem1VFS++7b+vPJ1c3J1YvAUXd8sGEl7clQu2BsYxPXQBBgh9iHFZXl3zlVgFPe6ZAGtJ2YnGYjKW1bKYnMKNKMp9zrV/pzoBCNAPMr7+GAmGt2MI6HTutjPgRNK8efPw6KOPYunSpejYsSMMBgO+/fZbPPbYY5g/f37A62XAqYRMJgMMogGSQQLguHpGNBhglCTApB92AKPyXA48ZbcGcB96ACjBB4BS4wNAU+uj/hfQr9LWq/JWnvtQ9e2trToS40l4arZRyng64Xn55eky3YdAEWcM7iTjS02XP/unG2587Fjqrmwoal8c88pPgPG2bmUdvpQp3Y5dEmExlp3c7ZKoqWk0qQKJc/hxlHf60WHS+dHh7e8wwNDj6T3wuqzTMTKWRC7gcBwcx/2url69ii5duig3/7Tb7TCbzRgzZozmnll//PGHz+tlwKmE4kxGiAYJcibQCztmOMKMHHYAuA08ANyGHqAsyLgLPzJ37f3qdThPdw423oKPev169KrQfeW8LW/V5L5wF1DUPAUMb7UpNlEKaD992S+v2/cjtLgr709wAQILL57WB4Q3wHhbv7IeP0KMtzJ2VeA1OTXVuPxwMEL5OwccNxYHyv5eLU6BXhAl+Nv64y7wBBNo3JGPtSGOp8ZIWrRoUVjWy3exEjIZDDCZSmtsAJewAyMgSaXTTIayIGNSXdZdWsMDuIYeeZrSr0bShhnBabpzAHLMc+2D49Ik5aYqHNCp0dH5knTX9u+tT0AwIShYvgYLwLeA5W+48ae8t5O7u3V5bMrz1HnWz2Yjb+sDggsvjvUHXwMDhC7A+LK+BGhrcLwtZxLdr0svELnjvC1ZoBds+3M8XPbFyCaqSBo1alRY1suAUwnJ3/dGOMKLc9gBAEECTKXzywKPpAQeuYYHcB964pUyZcEH0Nb6ANovNucQ5DxfHVScvzxdqsdFL3123PwydFfD42tnyEj0K3Dmy8nWWZzJ4NNrCqSGx5dmK2/hItDaFl/W7S1YhKLmxZftAL5fHRSqAOPM6HI7B9X/napb9JqXzB6ygN3oe/OJJcR9wYJh1xkPi8Jn//79iIuLQ5s2bQAAH3/8MVasWIFWrVph+vTpiI8PLOYy4FRCcaq2c6PJETjUYUcofQ54Djxyk5Ze6AG0wcfxvGwfnAOQ3nyZ3U3Ycf6ydQ08TpeXS57LO5aRdC979tQR2ddxKALtWxBq6pO/81UxzvMD3obPNRO+NJt4X5cvQSIUNS7+bA+IfngBXANMMOXjdYKr6OFz7RyQKgrBxwsHQrItUfLpYghPy1d0Dz/8MKZMmYI2bdrgl19+wdChQ3HXXXfhgw8+wNWrVwNuwmLAqYQMBqcv6NJztzrsAFACDwCXGh453KhDDyAHHyjBR14PoB9+lLLKdNVulU6P1zx3DUPO6wb0ams81+YA7gKPvFzZF7WnGhpfv2zKS9gJl0BCkq+hwZ/aqlAHFsC/gOFvM0m4wwtQVoMbKvL3hTdBXqxYtr0IZA9fB7mk0Dh+/DjatWsHAPjggw/Qs2dPrF69Gl999RXuueceBhzyj/p7Uf3lboLBpXYH0DZnAdCt5XFML1uP8oWmqvGRl4XqC8RdzY1jnn4Qcl7Oedl4OK/LqPsFq/frUy/8uOsf4K72xpeg426dnkSj+SsQgTSZqQXSf8KfkKJsx89lwh1YgMBCCxD4id95e8rffIg78Vakbi2hfu3kmSRJEEu/oLdt24ZBgwYBAOrXr4/z588HvF4GnEpIffIRJAnOf8ueAg/gvpYHKKvpAbTBR2nOKl2nvKxjIcc/6hAk75u7ICTvh+a5Xq2Ml1Cktx7XcOTYSXe/QN1V0XtqurJLok99DkI5DHu0qrIDCR6eBBIalGUD7HgazDYjHViC2aavy1bkAODLcfV3kE8KTqdOnfDSSy+hT58+2L59O5YtWwYAOHHiBNLT0wNeLwNOJWQ0GpQw4PxL21vgAdyHHkBbXS06rcjoHDYMzidcgyaQaGqBHCsHUNYM5ksYUn/A5SvBNPsgakOVsi6naepmOM10nbLydHdfkqIIxHsIN5rA5OVXr18ByFNn0ABqk4IVzFUuPq0/RMEq2JN5KJpUQhEoIhVKIth9xS/+1CoGWwPpD7sowhBE+12wA5WWB4sWLcLw4cPx0Ucf4dlnn8V1110HAPjnP/+J7OzsgNfLgFNJOd9U0l3gAQABridRvdADaGsJPIYf0bWdW93spVqxTs2MwaVmxl0YAjwEIsBrKFL2XzcYadepWa9e6HGqsXLZhsL3jpx6ISqQ7zvnwOWp42g0VdSTdCj3O6TrinAYiWRw8MbTjXU9zaPQa9u2LQ4fPuwy/ZVXXlFuKRMIBhwC4D7wAL6HHkC/OcJT+AH0A5BjH0qX9yUIQa9GSC6vs5/OgcixAwDUgUim6jukrEC/6cylxki7UdUy+ttw2Y7OfOdtulCdtAIPKoZyG3JCKWKBKYzbCWdIiUYgYbggWUJCQlDLM+BUQuovW3cnMb0vGW+hB3AffAAPNw3UCUCAfggCfA9CgPswBPgXiIDSQRD1GPVCEaBX06Qw6QSsUvIfpceAoVuzpcfDPnggitHvZ+Hp9Ud73wIRqdqSSIaSaIaRsIbGCvj5IlcMOJWcuysodMu6+TLzJfgAnsMP4GhucZsH1DUcHoIQ4FsYAvRrhvSWcSwnwV1NqV6fHZnbUASU3h7DPW9DYzj3cXLHue+TN55eq69CcbWXr5cfVxTRbp6J1TDiD19DZiSb7gRBgjGYcXDCcDf2WMGAQxp6X0Temip8CT6A9y94vQ7OeryOQuumRghwXysE+BeGAM+ByLF8YKFI3ransWQkyXsI8bZ/ztuTGf24gsRtDWAIwolvNVQVT3lugikvQQQov52VqeJgwCGvAgk9gPcvcn8DEOB7CAKCC0KA5zAEeA5EgPsaIr1lHcurasJ0wou2VsT9FVoybwFJu69ui+psu0w4B3nzJ2jpbrOc9yEqT2EiEOU5gARbW1bR3xtyYMChgHj6AvD1xOJvAAJ8/+LyJwh5ahpTtuslDAGuV425zHe6isxlGx4CkfPyZevxLai4BhTvAUnNn7CkJ9AAFYxAa5HKw1W35Tk8hEK0m+so+iZPnuxz2YULFwa0DQYcCrlQhB/A96r8YIMQgJDVCgHacYLc8RaGAO+BCPAeivTW5Vifm6vgvNYc6fEvLOkJNkCFku8hsfyqbAHCEOLXG+r1kasDBw5onu/btw+CIKB58+YAHLdvMJlM6NixY8DbYMChiPJW9RtIs4IvQcjtCd3HZjFZKIMQ4FsYArS3zfBYznmUaHfbVQUjbyduX8OR6za0zwMPCH5cIh9GcgiLdOAqrxgCQsMuiDAIQQz05+eyjRo1wqlTp1ymjx8/HkuXLnWZvnPnTjz99NP48ccfcfXqVTRs2BAPP/wwHn/8caVMTk4O7r//fpdlr1275vZS7//+97/K/xcuXIjk5GS8++67SEtLAwBcuHAB999/P26++Wa/Xp8aAw6VK760fZfHEAQEFoQkyY9bGfjxPeZrIAJ8D0Uy9f3I/KGtkQo8JKiDU6RrVUSRJ/Zoi0TzXSw3Ee7duxeCICjPjxw5gr59++Luu+/WLZ+UlIQJEyagbdu2SEpKws6dO/Hwww8jKSkJDz30kFIuJSUFx44d0yzr6zg2CxYswJYtW5RwAwBpaWl46aWX0K9fPzzxxBP+vEQFAw5VONEMQUDoaoOAMAUhOPoK+d1R0uh/YAm0NsVkCmx8Hv19iEzIESQppk98VDnUqlVL8/zll19G06ZN0bNnT93y7du3R/v27ZXnjRo1wocffogvv/xSE3AMBgMyMjIC2ier1Ypff/0VrVu31kwvKCjApUuXAlonwIBDMSpcIQiIfG0Q4F8QAvy/wWVAgQjwOxRpeBgjyFeO0BG+GhVfx3iqqCJdA1ZRjqGpAo7BZLVaNc8tFgssFovHZUpKSrBq1SpMnjzZ55rJAwcOYNeuXXjppZc00y9fvoyGDRtCEAS0a9cOM2fO1AQjT/785z/j/vvvx4IFC9C1a1cAwNdff42nnnoKd911l0/r0MOAQ5VWOPoDKesO4AoxtXAHIQCaK8f8rR2SBRKKlFtzBFkbIorhOWFqLueP8pg14a6dqiiBI5YJkuT3YJzOywNA/fr1NdOnTZuG6dOne1z2o48+wsWLFzF69Giv26lXrx5+++032O12TJ8+HQ888IAyr0WLFsjJyUGbNm1gtVrx2muvoXv37jh06BCaNWvmdd1vvvkmnnzySdx3332w2WwAALPZjLFjx+KVV17xurw7BqkS9JizWq1ITU1F/vlCpKSkRHt3KIaEc6yVUJ3cgv2VHoqX6EtHam/Ccayj0WG5Il2NVVldslrRsmEtFBaG75whn5f6vvofxCVWDXg9tmuXsfXxW3HmzBnNvvpSg9O/f3/Ex8fjk08+8bqdEydO4PLly/j6668xZcoUvP7667j33nt1y4qiiA4dOqBHjx5YvHixz6/lypUr+PnnnyFJEq677jokJSX5vKwe1uAQBSGatUCAbyEo0Nogmb8/8vVW42+TGaBzS44gaxt0B2sMcZ8aXwJTeao1YdiKHSkpKX6FsVOnTmHbtm348MMPfSrfuHFjAECbNm3w66+/Yvr06W4DjtFoROfOnfHTTz/5vD+Ao0Nz27Zt/VrGEwYcojAKZwACQheCgOCDkCzQZjKX/QmwecjtyNQhCBbeb1sS9Ca870MIa53KU9gqTyrDcVmxYgVq166NgQMH+r2sJEkoLi72OP/gwYNo06aNT+u7cuUKXn75ZfznP/9BQUEBRKcP+S+//OL3PgIMOERRFe4ABIQ2BAH+ffmHMgzJvI46HeJgpBbKIfwD7+Qesl0ISHkY6TmWCAJgCOpmm/4vI4oiVqxYgVGjRsFs1saAqVOnIjc3FytXrgQALF26FA0aNECLFi0AOMbFmT9/Ph599FFlmRdffBFdu3ZFs2bNYLVasXjxYhw8eFB3XB09DzzwALZv344RI0agTp06IRuKgQGHqByLRAACQh+CZKGqFVILRZOZnkCDkczffkbhvN9ROPuGRTtgRUKsv8Zt27bh9OnTGDNmjMu8vLw8nD59WnkuiiKmTp2KEydOwGw2o2nTpnj55Zfx8MMPK2UuXryIhx56CPn5+UhNTUX79u2xY8cO3HjjjT7tz6ZNm/Dvf/8b3bt3D/7FqbCTMVEMi8YNJyMxLk0k+o5E65sxFB2yI6m839Q0EJesVlxXr2ZEOhnfMv8/MCcG3pnWfu0KPn/y1rDua7g1btwYn376KVq2bBnS9bIGhyiGRaoGSLPNIAdM9EUom8ncCbSCJdhDGmxNklokwlJ5vfN2LAavWDVz5ky88MILePfdd1GlSpWQrZcBh6gSi0YAUrYdpmYxZ/52GA22dijY830oD3kow5JaRahlCiZ4RTK02QURiOC9qMqjBQsW4Oeff0Z6ejoaNWqEuLg4zfz9+/cHtF4GHCJyK5oBCPBvoL1QNY0FcgVNKJvMylNAcidcwUlPRQhTFJw777wzLOtlwCGigIXzlhj+ikTTmDvRDkVqoap8KC8tPJEMU7Joj2Bd2UybNi0s62XAIaKwinYtkLNo1ArpCXSslUgNzhfqVpryEpio8mDAIaKoKk+1QM7KSxhSC2YQumiOXByubi0VPTgJohTcODgVtAmvevXqOH78OGrWrIm0tDSPY9/88ccfAW2DAYeIyr3yHIJk5TEMOauo4ciTcASncnphWEx59dVXkZycrPw/VIP7qTHgEFFMqAghSOZvH49oBSK1UNy+oLyGJIq8UaNGKf/35W7mgWDAIaJKoyKFILVAOr2Wh1DkLFT3eGJQii3Dhw9Hr1690LNnT1x//fUhWy8DDhGRSkUNQc4qYi2Rr0J5M8xohyVBEGEIYiwbIQbGwalatSoWLFiAhx9+GBkZGejZsyd69uyJXr16KffACkSM33GDiCj0jAaDT4+KxGg0BPSo6EwGg+6DIuett97Cjz/+iHPnzmHhwoVITU3Fa6+9htatW6NOnToBr5c1OEREYRIrtUGeBBpyKlKNEUVGcnIy0tLSkJaWhmrVqsFsNiMjIyPg9THgEBFFka81PRU9CDljMCLZ008/je3bt+PQoUPIyspCjx49MHXqVPTo0QPVqlULeL0MOEREFYA/TV6xFobUgmkWYzgqn1555RXUqlUL06ZNwx133BGyu4oz4BARxZjKWivkja/hKJJ9i9jJGDhw4AC2b9+OL774AgsWLIDJZFI6Gffq1SvgwMOAQ0RUSbFWiMqDG264ATfccAMmTpwIADh06BAWLVqEiRMnQhRFCIIQ0HoZcIiIyCuGIQqnAwcO4IsvvsAXX3yBL7/8ElarFe3atUPv3r0DXicDDhERhRTDEPkjLS0Nly9fxg033IBevXrhwQcfRI8ePZCSkhLUehlwiIgoaip7GBIFCUIQN9sUg1i2vHjvvfdCEmichW2gv5MnT2Ls2LFo3LgxEhMT0bRpU0ybNg0lJSWacqdPn8bgwYORlJSEmjVrYuLEiS5lDh8+jJ49eyIxMRF169bFjBkzIMXgB52IiNzzdYDFijjQYmU2aNCgkIcbIIw1OD/++CNEUcRbb72F6667DkeOHMGDDz6IK1euYP78+QAAQRAwcOBA1KpVCzt37sTvv/+OUaNGQZIkLFmyBABgtVrRt29f9O7dG3v37sXx48cxevRoJCUl4YknngjX7hMRUQXnb8iJxRqiyixsAWfAgAEYMGCA8rxJkyY4duwYli1bpgScLVu24Pvvv8eZM2eQmZkJAFiwYAFGjx6NWbNmISUlBe+//z6KioqQk5MDi8WCrKwsHD9+HAsXLsTkyZPDcot1IiKqfORAxNqf2BDRe1EVFhaievXqyvPdu3cjKytLCTcA0L9/fxQXF2Pfvn1KmZ49e8JisWjKnDt3DidPnozYvhMREYWaIIhBP0hfxALOzz//jCVLlmDcuHHKtPz8fKSnp2vKpaWlIT4+Hvn5+W7LyM/lMs6Ki4thtVo1DyIiIqo8/G6imj59Ol588UWPZfbu3YtOnTopz8+dO4cBAwbg7rvvxgMPPKApq9fEJEmSZrpzGbmDsbvmqTlz5ujuY2Kc40FEROSOjeeJmOB3wJkwYQLuuecej2UaNWqk/P/cuXPo3bs3unXrhuXLl2vKZWRk4JtvvtFMu3DhAmw2m1JLk5GR4VJTU1BQAAAuNTuyqVOnYvLkycpzq9WK+vXre35hREREFDP8bqKqWbMmWrRo4fGRkJAAAMjNzUWvXr3QoUMHrFixAkajdnPdunXDkSNHkJeXp0zbsmULLBYLOnbsqJTZsWOH5tLxLVu2IDMzUxOk1CwWC1JSUjQPIiKi8kYUpaAf/srNzcV9992HGjVqoEqVKmjXrp3S79WdpUuXomXLlkhMTETz5s2xcuVKlzLr169Hq1atYLFY0KpVK2zYsMHvfQulsPXBOXfuHHr16oX69etj/vz5+O2335Cfn6+pjenXrx9atWqFESNG4MCBA/jPf/6DJ598Eg8++KASSoYNGwaLxYLRo0fjyJEj2LBhA2bPns0rqIiIiPx04cIFdO/eHXFxcdi0aRO+//57LFiwANWqVXO7zLJlyzB16lRMnz4dR48exYsvvohHHnkEn3zyiVJm9+7dGDp0KEaMGIFDhw5hxIgRGDJkiEsrTSQZpDCNmJeTk4P7779fd556k6dPn8b48ePx+eefIzExEcOGDcP8+fM1V00dPnwYjzzyCPbs2YO0tDSMGzcOL7zwgs8Bx2q1IjU1FYWFhazNISIijyJxzpC30XbqRpgSkgJej1B0Bd/Nud3nfZ0yZQq++uorfPnllz5vIzs7G927d8crr7yiTJs0aRK+/fZb7Ny5EwAwdOhQWK1WbNq0SSkzYMAApKWlYc2aNX68otAJ2zg4o0ePxujRo72Wa9CgAf71r395LNOmTRvs2LEjRHtGREQUW5yvFrZYLJqKAtnGjRvRv39/3H333di+fTvq1q2L8ePH48EHH3S77uLiYqXriSwxMRF79uyBzWZDXFwcdu/ejccff1xTpn///li0aFHgLypIER0Hh4iIiMoIouNeVAE/Svvg1K9fH6mpqcpjzpw5utv75ZdfsGzZMjRr1gybN2/GuHHjMHHiRN0+NbL+/fvj//2//4d9+/ZBkiR8++23eOedd2Cz2XD+/HkA7od0cTecSyTwZptEREQV3JkzZzRNVHq1NwAgiiI6deqE2bNnAwDat2+Po0ePYtmyZRg5cqTuMs8//zzy8/PRtWtXSJKE9PR0jB49GvPmzYPJZFLK6Q3pEs2+sqzBISIiquCcrxx2F3Dq1KmDVq1aaaa1bNkSp0+fdrvuxMREvPPOO7h69SpOnjyJ06dPo1GjRkhOTkbNmjUBuB/Sxd1wLpHAgENERFRJdO/eHceOHdNMO378OBo2bOh12bi4ONSrVw8mkwlr167FoEGDlOFfunXrhq1bt2rKb9myBdnZ2aHbeT+xiYqIiChKBEEEgriflL/3onr88ceRnZ2N2bNnY8iQIdizZw+WL1+uGYh36tSpyM3NVfrlHD9+HHv27EGXLl1w4cIFLFy4EEeOHMG7776rLPPYY4+hR48emDt3Lu644w58/PHH2LZtm3KVVTSwBoeIiKiS6Ny5MzZs2IA1a9YgKysLM2fOxKJFizB8+HClTF5enqbJShAELFiwADfccAP69u2LoqIi7Nq1SzPYbnZ2NtauXYsVK1agbdu2yMnJwbp169ClS5dIvjyNsI2DU55wHBwiIvJVJMfBafHkBpgsQYyDU3wFP87/M89vOliDQ0RERDGHfXCIiIiixG4XIZmC6INjD3zZWMcaHCIiIoo5DDhEREQUcxhwiIiIKOYw4BAREVHMYSdjIiKiKBEFCRACH61FDGLZWMcaHCIiIoo5DDhEREQUcxhwiIiIKOawDw4REVGUCIIEKYibbbIPjnuswSEiIqKYw4BDREREMYcBh4iIiGIO++AQERFFiSiIQFB9cHizTXdYg0NEREQxhwGHiIiIYg4DDhEREcUc9sEhIiKKEkEUIAlCwMuLYuDLxjrW4BAREVHMYcAhIiKimMOAQ0RERDGHfXCIiIiiRBIlSGLg95MKZtlYxxocIiIiijkMOERERBRzGHCIiIgo5jDgEBERRYkoiEE//JWbm4v77rsPNWrUQJUqVdCuXTvs27fPp2W/+uormM1mtGvXTjM9JycHBoPB5VFUVOT3/oUKOxkTERFVEhcuXED37t3Ru3dvbNq0CbVr18bPP/+MatWqeV22sLAQI0eOxK233opff/3VZX5KSgqOHTummZaQkBCqXfcbAw4REVElMXfuXNSvXx8rVqxQpjVq1MinZR9++GEMGzYMJpMJH330kct8g8GAjIyMEO1p8NhERUREVEls3LgRnTp1wt13343atWujffv2+Mc//uF1uRUrVuDnn3/GtGnT3Ja5fPkyGjZsiHr16mHQoEE4cOBAKHfdbww4REREFZzVatU8iouLdcv98ssvWLZsGZo1a4bNmzdj3LhxmDhxIlauXOl23T/99BOmTJmC999/H2azfsNPixYtkJOTg40bN2LNmjVISEhA9+7d8dNPP4Xk9QWCTVRERERRIghB3myzdNn69etrpk+bNg3Tp093LS+K6NSpE2bPng0AaN++PY4ePYply5Zh5MiRuvs3bNgwvPjii7j++uvd7kfXrl3RtWtX5Xn37t3RoUMHLFmyBIsXLw7kpQWNAYeIiKiCO3PmDFJSUpTnFotFt1ydOnXQqlUrzbSWLVti/fr1uuUvXbqEb7/9FgcOHMCECRMAOEKSJEkwm83YsmULbrnlFpfljEYjOnfuzBocIiIiClxKSoom4LjTvXt3lyudjh8/joYNG7pd7+HDhzXT3njjDXz++ef45z//icaNG+suJ0kSDh48iDZt2vj4CkKPAYeIiKiSePzxx5GdnY3Zs2djyJAh2LNnD5YvX47ly5crZaZOnYrc3FysXLkSRqMRWVlZmnXUrl0bCQkJmukvvvgiunbtimbNmsFqtWLx4sU4ePAgli5dGrHX5owBh4iIKEpEQQQCGKxPs7wfOnfujA0bNmDq1KmYMWMGGjdujEWLFmH48OFKmby8PJw+fdqv9V68eBEPPfQQ8vPzkZqaivbt22PHjh248cYb/VpPKBkkSYr5W5FarVakpqaisLDQpyo8IiKqvCJxzpC3UX3YOzDGVwl4PWLJVfyxegzPbzp4mTgRERHFHAYcIiIiijnsg0NERBQlUoA3zFQvT/pYg0NEREQxhwGHiIiIYg4DDhEREcUc9sEhIiKKEkEUYQjiXlSSyD447rAGh4iIiGIOAw4RERHFHAYcIiIiijnsg0NERBQloiDCYOQ4OOHAGhwiIiKKOREJOMXFxWjXrh0MBgMOHjyomXf69GkMHjwYSUlJqFmzJiZOnIiSkhJNmcOHD6Nnz55ITExE3bp1MWPGDFSCe4QSERFRgCLSRPX3v/8dmZmZOHTokGa6IAgYOHAgatWqhZ07d+L333/HqFGjIEkSlixZAsBxx9W+ffuid+/e2Lt3L44fP47Ro0cjKSkJTzzxRCR2n4iIiCqYsAecTZs2YcuWLVi/fj02bdqkmbdlyxZ8//33OHPmDDIzMwEACxYswOjRozFr1iykpKTg/fffR1FREXJycmCxWJCVlYXjx49j4cKFmDx5MgwGQ7hfAhERUVgIggCDMYhxcIIYQyfWhbWJ6tdff8WDDz6I9957D1WqVHGZv3v3bmRlZSnhBgD69++P4uJi7Nu3TynTs2dPWCwWTZlz587h5MmTutstLi6G1WrVPIiIiKjyCFvAkSQJo0ePxrhx49CpUyfdMvn5+UhPT9dMS0tLQ3x8PPLz892WkZ/LZZzNmTMHqampyqN+/frBvhwiIiKqQPwOONOnT4fBYPD4+Pbbb7FkyRJYrVZMnTrV4/r0mpgkSdJMdy4jdzB21zw1depUFBYWKo8zZ874+zKJiIioAvO7D86ECRNwzz33eCzTqFEjvPTSS/j66681TUsA0KlTJwwfPhzvvvsuMjIy8M0332jmX7hwATabTamlycjIcKmpKSgoAACXmh2ZxWJx2S4REVF5I4kSIAZ+VbAUxLKxzu+AU7NmTdSsWdNrucWLF+Oll15Snp87dw79+/fHunXr0KVLFwBAt27dMGvWLOTl5aFOnToAHB2PLRYLOnbsqJR55plnUFJSgvj4eKVMZmYmGjVq5O/uExERUSUQtj44DRo0QFZWlvK4/vrrAQBNmzZFvXr1AAD9+vVDq1atMGLECBw4cAD/+c9/8OSTT+LBBx9ESkoKAGDYsGGwWCwYPXo0jhw5gg0bNmD27Nm8goqIiIjciupIxiaTCf/+97+RkJCA7t27Y8iQIbjzzjsxf/58pUxqaiq2bt2Ks2fPolOnThg/fjwmT56MyZMnR3HPiYiIqDyL2L2oGjVqpDv6cIMGDfCvf/3L47Jt2rTBjh07wrVrREREFGN4s00iIqIokQQ7YLQHtzzp4s02iYiIKOYw4BAREVHMYcAhIiKimMOAQ0REFC2CPfiHn3Jzc3HfffehRo0aqFKlCtq1a6fc/9Gd7du3o2PHjkhISECTJk3w5ptvupRZv349WrVqBYvFglatWmHDhg1+71soMeAQERFVEhcuXED37t0RFxeHTZs24fvvv8eCBQtQrVo1t8ucOHECt912G26++WYcOHAAzzzzDCZOnIj169crZXbv3o2hQ4dixIgROHToEEaMGIEhQ4a43K0gkgyS3rXbMcZqtSI1NRWFhYXKAIJERER6InHOkLdh6T8fhrjEgNcj2a6hePOTPu/rlClT8NVXX+HLL7/0eRtPP/00Nm7ciB9++EGZNm7cOBw6dAi7d+8GAAwdOhRWqxWbNm1SygwYMABpaWlYs2aNH68odFiDQ0REVMFZrVbNo7i4WLfcxo0b0alTJ9x9992oXbs22rdvj3/84x8e1717927069dPM61///749ttvYbPZPJbZtWtXEK8qOAw4RERE0SLYAcEWxMPRB6d+/fpITU1VHnPmzNHd3C+//IJly5ahWbNm2Lx5M8aNG4eJEydi5cqVbncxPz/f5ebW6enpsNvtOH/+vMcyzjfLjiQO9EdERFTBnTlzRtNEZbFYdMuJoohOnTph9uzZAID27dvj6NGjWLZsGUaOHOl2/c73fpR7t6in65WJ5j0jWYNDRERUwaWkpGge7gJOnTp10KpVK820li1b4vTp027XnZGR4VITU1BQALPZjBo1angs41yrE0kMOERERJVE9+7dcezYMc2048ePo2HDhm6X6datG7Zu3aqZtmXLFnTq1AlxcXEey2RnZ4doz/3HgENERBQtYjD9b2yO5f3w+OOP4+uvv8bs2bPxv//9D6tXr8by5cvxyCOPKGWmTp2qaa4aN24cTp06hcmTJ+OHH37AO++8g7fffhtPPvmkUuaxxx7Dli1bMHfuXPz444+YO3cutm3bhkmTJgV9iALFgENERFRJdO7cGRs2bMCaNWuQlZWFmTNnYtGiRRg+fLhSJi8vT9Nk1bhxY3z66af44osv0K5dO8ycOROLFy/GX/7yF6VMdnY21q5dixUrVqBt27bIycnBunXr0KVLl4i+PjWOg0NERKQS0XFwbpkJgzkh4PVI9iIUf/48z286WINDREREMYeXiRMREUWLYAcM/t9PSrM86WINDhEREcUcBhwiIiKKOQw4REREFHPYB4eIiChaBBtgMAW3POliDQ4RERHFHAYcIiIiijkMOERERBRzGHCIiIgo5rCTMRERUbTY7QCC6Chs50B/7rAGh4iIiGIOAw4RERHFHAYcIiIiijnsg0NERBQtouB4BLM86WINDhEREcUcBhwiIiKKOQw4REREFHPYB4eIiChaBHuQN9vkODjusAaHiIiIYg4DDhEREcUcBhwiIiKKOeyDQ0REFC2iDRCCqGsQg7iPVYxjDQ4RERHFHAYcIiIiijkMOERERBRzGHCIiIiiRRAcY9kE/PDvXlTTp0+HwWDQPDIyMtyW/+KLL1zKGwwG/Pjjj0qZnJwc3TJFRUUBH5ZQYCdjIiKiSqR169bYtm2b8txk8j7Q4LFjx5CSkqI8r1WrlmZ+SkoKjh07ppmWkJAQ5J4GhwGHiIioEjGbzR5rbfTUrl0b1apVczvfW01QNFSKgCNJEgDAarVGeU+IiKi8k88V8rkjrIQSBLUVoQSA6/nNYrHAYrHoLvLTTz8hMzMTFosFXbp0wezZs9GkSROPm2nfvj2KiorQqlUrPPfcc+jdu7dm/uXLl9GwYUMIgoB27dph5syZaN++fRAvLASkSuDnn3+WAPDBBx988MGHz4+ff/45bOela9euSRkZGSHZz6pVq7pMmzZtmu52P/30U+mf//yn9N1330lbt26VevbsKaWnp0vnz5/XLf/jjz9Ky5cvl/bt2yft2rVL+tvf/iYZDAZp+/btSpndu3dL7733nnTw4EFpx44d0l/+8hcpMTFROn78eDgOnc8MkhSJiBpdFy9eRFpaGk6fPo3U1NRo707UWK1W1K9fH2fOnNG0pVY2PA4OPA5leCwceBwcCgsL0aBBA1y4cMFjs0ywioqKUFJSEvR6JEmCwWDQTPNUg6N25coVNG3aFH//+98xefJkn7Y3ePBgGAwGbNy4UXe+KIro0KEDevTogcWLF/u0znCoFE1URqPjYrHU1NRK/UcrS0lJ4XEAj4OMx6EMj4UDj4ODfO4Il4SEhKh3xE1KSkKbNm3w008/+bxM165dsWrVKrfzjUYjOnfu7Nc6w4GXiRMREVVSxcXF+OGHH1CnTh2flzlw4IDH8pIk4eDBg36tMxwqRQ0OERERAU8++SQGDx6MBg0aoKCgAC+99BKsVitGjRoFAJg6dSpyc3OxcuVKAMCiRYvQqFEjtG7dGiUlJVi1ahXWr1+P9evXK+t88cUX0bVrVzRr1gxWqxWLFy/GwYMHsXTp0qi8RlmlCDgWiwXTpk3zqT0ylvE4OPA4OPA4lOGxcOBxcIjl43D27Fnce++9OH/+PGrVqoWuXbvi66+/RsOGDQEAeXl5OH36tFK+pKQETz75JHJzc5GYmIjWrVvj3//+N2677TalzMWLF/HQQw8hPz8fqampaN++PXbs2IEbb7wx4q9PrVJ0MiYiIqLKhX1wiIiIKOYw4BAREVHMYcAhIiKimMOAQ0RERDEnZgLOyZMnMXbsWDRu3BiJiYlo2rQppk2b5jJK5OnTpzF48GAkJSWhZs2amDhxokuZw4cPo2fPnkhMTETdunUxY8aMyNyTJMzeeOMNNG7cGAkJCejYsSO+/PLLaO9SyMyZMwedO3dGcnIyateujTvvvNPlzraSJGH69OnIzMxEYmIievXqhaNHj2rKFBcX49FHH0XNmjWRlJSE22+/HWfPno3kSwmpOXPmwGAwYNKkScq0ynIccnNzcd9996FGjRqoUqUK2rVrh3379inzK8NxsNvteO6555TvxSZNmmDGjBkQRVEpE6vHYceOHRg8eDAyMzNhMBjw0UcfaeaH6nVfuHABI0aMQGpqKlJTUzFixAhcvHgxzK+OfBKdO0SE3qZNm6TRo0dLmzdvln7++Wfp448/lmrXri098cQTShm73S5lZWVJvXv3lvbv3y9t3bpVyszMlCZMmKCUKSwslNLT06V77rlHOnz4sLR+/XopOTlZmj9/fjReVsisXbtWiouLk/7xj39I33//vfTYY49JSUlJ0qlTp6K9ayHRv39/acWKFdKRI0ekgwcPSgMHDpQaNGggXb58WSnz8ssvS8nJydL69eulw4cPS0OHDpXq1KkjWa1Wpcy4ceOkunXrSlu3bpX2798v9e7dW7rhhhsku90ejZcVlD179kiNGjWS2rZtKz322GPK9MpwHP744w+pYcOG0ujRo6VvvvlGOnHihLRt2zbpf//7n1KmMhyHl156SapRo4b0r3/9Szpx4oT0wQcfSFWrVpUWLVqklInV4/Dpp59Kzz77rLR+/XoJgLRhwwbN/FC97gEDBkhZWVnSrl27pF27dklZWVnSoEGDIvUyyYOYCTh65s2bJzVu3Fh5/umnn0pGo1HKzc1Vpq1Zs0ayWCxSYWGhJEmS9MYbb0ipqalSUVGRUmbOnDlSZmamJIpi5HY+xG688UZp3LhxmmktWrSQpkyZEqU9Cq+CggIJgHJDOFEUpYyMDOnll19WyhQVFUmpqanSm2++KUmSJF28eFGKi4uT1q5dq5TJzc2VjEaj9Nlnn0X2BQTp0qVLUrNmzZSb6ckBp7Ich6efflq66aab3M6vLMdh4MCB0pgxYzTT7rrrLum+++6TJKnyHAfngBOq1/39999LAKSvv/5aKbN7924JgPTjjz+G+VWRNzHTRKWnsLAQ1atXV57v3r0bWVlZyMzMVKb1798fxcXFStX17t270bNnT80AT/3798e5c+dw8uTJiO17KJWUlGDfvn3o16+fZnq/fv2wa9euKO1VeBUWFgKA8v6fOHEC+fn5mmNgsVjQs2dP5Rjs27cPNptNUyYzMxNZWVkV7jg98sgjGDhwIPr06aOZXlmOw8aNG9GpUyfcfffdqF27Ntq3b49//OMfyvzKchxuuukm/Oc//8Hx48cBAIcOHcLOnTuVQdoqy3FwFqrXvXv3bqSmpqJLly5Kma5duyI1NbXCHptYErMjGf/8889YsmQJFixYoEzLz89Henq6plxaWhri4+ORn5+vlGnUqJGmjLxMfn4+GjduHN4dD4Pz589DEASX156enq687lgiSRImT56Mm266CVlZWQCgvE69Y3Dq1CmlTHx8PNLS0lzKVKTjtHbtWuzfvx979+51mVdZjsMvv/yCZcuWYfLkyXjmmWewZ88eTJw4ERaLBSNHjqw0x+Hpp59GYWEhWrRoAZPJBEEQMGvWLNx7770AKs/nwVmoXnd+fj5q167tsv7atWtX2GMTS8p9Dc706dNhMBg8Pr799lvNMufOncOAAQNw991344EHHtDMc76lPOB6q3nnMlJpB2O9ZSsSvddV0V+TngkTJuC7777DmjVrXOYFcgwq0nE6c+YMHnvsMaxatcrjXYpj/TiIoogOHTpg9uzZaN++PR5++GE8+OCDWLZsmaZcrB+HdevWYdWqVVi9ejX279+Pd999F/Pnz8e7776rKRfrx8GdULxuX84pFB3lPuBMmDABP/zwg8eH/CsdcISb3r17o1u3bli+fLlmXRkZGS6p+sKFC7DZbEqS1ytTUFAAwDXtVxQ1a9aEyWTSfV0V9TW58+ijj2Ljxo3473//i3r16inTMzIyAMDjMcjIyEBJSQkuXLjgtkx5t2/fPhQUFKBjx44wm80wm83Yvn07Fi9eDLPZrKmNVIu141CnTh20atVKM61ly5bKPXYqy+fhqaeewpQpU3DPPfegTZs2GDFiBB5//HHMmTMHQOU5Ds5C9bozMjLw66+/uqz/t99+q7DHJpaU+4BTs2ZNtGjRwuND/qWam5uLXr16oUOHDlixYgWMRu3L69atG44cOYK8vDxl2pYtW2CxWNCxY0elzI4dOzSXjm/ZsgWZmZkuTVcVRXx8PDp27IitW7dqpm/duhXZ2dlR2qvQkiQJEyZMwIcffojPP//cpSmxcePGyMjI0ByDkpISbN++XTkGHTt2RFxcnKZMXl4ejhw5UmGO06233orDhw/j4MGDyqNTp04YPnw4Dh48iCZNmlSK49C9e3eXYQKOHz+u3FCwsnwerl696vI9aDKZlMvEK8txcBaq192tWzcUFhZiz549SplvvvkGhYWFFfbYxJTI92sOj9zcXOm6666TbrnlFuns2bNSXl6e8pDJl4nfeuut0v79+6Vt27ZJ9erV01wmfvHiRSk9PV269957pcOHD0sffvihlJKSEjOXib/99tvS999/L02aNElKSkqSTp48Ge1dC4m//e1vUmpqqvTFF19o3vurV68qZV5++WUpNTVV+vDDD6XDhw9L9957r+5lofXq1ZO2bdsm7d+/X7rlllvK/eWw3qivopKkynEc9uzZI5nNZmnWrFnSTz/9JL3//vtSlSpVpFWrVillKsNxGDVqlFS3bl3lMvEPP/xQqlmzpvT3v/9dKROrx+HSpUvSgQMHpAMHDkgApIULF0oHDhxQhsYI1eseMGCA1LZtW2n37t3S7t27pTZt2vAy8XIiZgLOihUrJAC6D7VTp05JAwcOlBITE6Xq1atLEyZM0FwSLkmS9N1330k333yzZLFYpIyMDGn69OkV+hJx2dKlS6WGDRtK8fHxUocOHZRLqGOBu/d+xYoVShlRFKVp06ZJGRkZksVikXr06CEdPnxYs55r165JEyZMkKpXry4lJiZKgwYNkk6fPh3hVxNazgGnshyHTz75RMrKypIsFovUokULafny5Zr5leE4WK1W6bHHHpMaNGggJSQkSE2aNJGeffZZqbi4WCkTq8fhv//9r+53wqhRoyRJCt3r/v3336Xhw4dLycnJUnJysjR8+HDpwoULEXqV5IlBkmJgiF4iIiIilXLfB4eIiIjIXww4REREFHMYcIiIiCjmMOAQERFRzGHAISIiopjDgENEREQxhwGHiIiIYg4DDhEREcUcBhwiIiKKOQw4REREFHMYcIiIiCjmMOAQERFRzPn/eK7LXuxTyWgAAAAASUVORK5CYII=\n",
                        "text/plain": [
                            "<Figure size 640x480 with 2 Axes>"
                        ]
                    },
                    "metadata": {},
                    "output_type": "display_data"
                }
            ],
            "source": [
                "x,y = rectangle(3,3, wt.diameter()*5)\n",
                "wfm(x,y,wd=[270],ws=10, yaw=[20,-10,0], tilt=0).flow_map().plot_wake_map()"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "08aa0f26",
            "metadata": {},
            "source": [
                "#### Gradients of AEP\n",
                "The gradients of the AEP can be computed by the `aep_gradients` method of `WindFarmModel` with respect to most of the input arguments. "
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 13,
            "id": "b6c604b5",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "Gradients of AEP wrt. x [array([-1.14696413e-03, -7.80093407e-05,  1.22497347e-03])]\n",
                        "Gradients of AEP wrt. y [array([ 0.00035313, -0.00070408,  0.00035094])]\n",
                        "Gradients of AEP wrt. ['x', 'y'] [array([-1.14696413e-03, -7.80093407e-05,  1.22497347e-03]), array([ 0.00035313, -0.00070408,  0.00035094])]\n",
                        "Gradients of AEP wrt. h [array([-2.11882021e-04, -4.71201387e-06,  2.16594034e-04])]\n"
                    ]
                }
            ],
            "source": [
                "for wrt_arg in ['x','y',['x','y'],'h']:\n",
                "    daep = wfm.aep_gradients(gradient_method=autograd, wrt_arg=wrt_arg)(x=x,y=y, h=[69,70,71], yaw=[20,-10,1], tilt=0)\n",
                "    print (f\"Gradients of AEP wrt. {wrt_arg}\", daep)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "341ca41e",
            "metadata": {},
            "source": [
                "**AEP gradients with respect to (x,y) or (xy)**\n",
                "\n",
                "When computing gradients with autograd, a significant speed up (40-50%) can be obtained by computing the gradients with respect to both `x` and `y` in one go:\n",
                "\n",
                "```\n",
                "wfm.aep_gradients(gradient_method=autograd, wrt_arg=['x','y'])(x,y)\n",
                "```\n",
                "\n",
                "Instead of first computing with respect to `x` and then with respect to `y`,\n",
                "\n",
                "```\n",
                "wfm.aep_gradients(gradient_method=autograd, wrt_arg='x')(x,y)\n",
                "wfm.aep_gradients(gradient_method=autograd, wrt_arg='y')(x,y)\n",
                "```\n",
                "\n",
                "Functionality to do this automatically under the hood has been implemented in the autograd function.\n",
                "\n",
                "For finite difference and complex step, the speed is similar."
            ]
        },
        {
            "cell_type": "markdown",
            "id": "cc3d8958",
            "metadata": {},
            "source": [
                "    from tqdm.notebook import tqdm\n",
                "    wfm = BastankhahGaussian(site, wt)\n",
                "\n",
                "    def get_aep(wrt_arg_lst, method):\n",
                "        return lambda x,y: [wfm.aep_gradients(gradient_method=method, wrt_arg=wrt_arg)(x,y) for wrt_arg in wrt_arg_lst]\n",
                "\n",
                "    N_lst = np.arange(100,600,100) # number of wt\n",
                "    D = wt.diameter()\n",
                "    method=autograd\n",
                "    res = [(wrt_arg_lst,method, [np.mean(timeit(get_aep(wrt_arg_lst, method=method), min_runs=1)(*rectangle(N,5,D*5))[1]) \n",
                "                                 for N in tqdm(N_lst)])\n",
                "           for wrt_arg_lst in (['x','y'],[['x','y']])]\n",
                "\n",
                "    ax1,ax2 = plt.subplots(1,2, figsize=(12,4))[1]\n",
                "    ax1.plot(N_lst, res[0][2], label=f\"Wrt. (x), (y), {res[0][1].__name__}\")[0].get_color()\n",
                "    ax1.plot(N_lst, res[1][2], label=f\"Wrt. (x, y), {res[1][1].__name__}\")\n",
                "    ax2.plot(N_lst, (np.array(res[0][2]) - res[1][2])/res[0][2]*100)\n",
                "\n",
                "    setup_plot(ax=ax1, title='Time to compute AEP gradients', ylabel='Time [s]', xlabel='Number of wind turbines')\n",
                "    setup_plot(ax=ax2, title=\"Speedup of (xy) compared to (x,y)\", ylabel='Speedup [%]', xlabel='Number of wind turbines', ylim=[0,60])"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "dc244d14",
            "metadata": {},
            "source": [
                "![image2.png](images/Optimization_xy.svg)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "a68caa07",
            "metadata": {},
            "source": [
                "**Gradients of WS, TI, Power and custom functions**\n",
                "\n",
                "The normal `WindFarmModel.__call__` method, which is invoked by `wfm(x,y,...)` returns a xarray Dataset SimulationResult. This step breaks the autograd data flow. We therefore need to specify the argument `return_simulationResult=False`.\n",
                "\n",
                "The relevant output is:\n",
                "\n",
                "    WS_eff_ilk, TI_eff_ilk, power_ilk, ct_ilk, *_ = WindFarmModel(..., return_simulationResult=False)\n",
                "\n",
                "**Below are a two basic examples**"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "739818e1",
            "metadata": {},
            "source": [
                "**1) Mean power wrt (x,y) - 2 x 1D inputs, one output**\n",
                "\n",
                "Compute the gradients of the mean power with respect to both x and y.\n",
                "\n",
                "Note, there is no need to convert it to a one-merged-input function, as the autograd method in PyWake does this under the hood"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 16,
            "id": "563ed183",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "AEP Gradients: [array([-1.90426671e+01,  1.77635684e-15,  1.90426671e+01]), array([ 1.14162970e-13, -4.65754814e-14, -6.75874890e-14])]\n",
                        "(2, 3)\n"
                    ]
                }
            ],
            "source": [
                "def mean_power(x,y):\n",
                "    power_ilk = wfm(x=x, y=y, yaw=0, tilt=0, return_simulationResult=False)[2] # index 2 = power_ilk\n",
                "    return power_ilk.mean()\n",
                "\n",
                "mean_power_gradients_function = autograd(mean_power,vector_interdependence=True, argnum=[0,1])\n",
                "d_aep = mean_power_gradients_function(x, y)\n",
                "\n",
                "print ('AEP Gradients:',d_aep)\n",
                "print (np.shape(d_aep))"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "24a8ca98",
            "metadata": {},
            "source": [
                "**2) Power per wind speed wrt. x - 1D input, 1D output**\n",
                "\n",
                "Compute the gradients of the power per wind speed (i.e. power meaned over wind turbine and direction) with respect to x."
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 19,
            "id": "c43dd8e6",
            "metadata": {},
            "outputs": [
                {
                    "data": {
                        "text/plain": [
                            "(23, 3)"
                        ]
                    },
                    "execution_count": 19,
                    "metadata": {},
                    "output_type": "execute_result"
                }
            ],
            "source": [
                "def ws_power(x):\n",
                "    power_ilk = wfm(x=x, y=y, yaw=0, tilt=0, return_simulationResult=False)[2] # index 2 = power_ilk\n",
                "    return power_ilk.mean((0,1)) # mean power pr wind speed\n",
                "\n",
                "ws_power_gradients_function = autograd(ws_power,vector_interdependence=True)\n",
                "np.shape(ws_power_gradients_function(x))"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "4c8de853",
            "metadata": {},
            "source": [
                "**Manual gradient functions for autograd**\n",
                "\n",
                "Autograd can be supplemented with custom gradient functions, that bypass the automatic differentiation process and returns the gradients directly.\n",
                "This is usefull for functions that cannot be analytically differentiated by autograd, e.g. interpolation functions. Some commonly used functions have been implemented in `py_wake.utils.gradients`, e.g.\n",
                "\n",
                "- trapz (np.trapz)\n",
                "- interp (np.interp)\n",
                "- PchipInterpolator (scipy.PchipInterpolator)\n",
                "- UnivariateSpline (scipy.UnivariateSpline)\n",
                "\n",
                "\n",
                "Specifying the gradient functions and ensuring that they return the gradients in the right dimensions is, however, not trivial. \n",
                "\n",
                "It was expected that the computational time could be reduced by specifying maually-implemented gradient functions of some time-critical functions. An example is shown below, where functions to calculate the gradients of `calc_deficit` of the `BastankhahGaussianDeficit` with respect to all inputs are implemented."
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 20,
            "id": "90122db9",
            "metadata": {},
            "outputs": [],
            "source": [
                "from py_wake.deficit_models.gaussian import BastankhahGaussianDeficit\n",
                "from py_wake.utils.gradients import set_vjp\n",
                "from py_wake.utils.model_utils import method_args\n",
                "import warnings\n",
                "\n",
                "class BastankhahGaussianDeficitGradients(BastankhahGaussianDeficit):\n",
                "    def __init__(self, k=0.0324555, ceps=.2, use_effective_ws=False):\n",
                "        BastankhahGaussianDeficit.__init__(self, k=k, ceps=ceps, use_effective_ws=use_effective_ws)\n",
                "        self._additional_args = method_args(self.calc_deficit)\n",
                "        self.use_effective_ws = use_effective_ws\n",
                "        self.calc_deficit = set_vjp([self.get_ddeficit_dx(i) for i in range(6)])(self.calc_deficit)\n",
                "\n",
                "    @property\n",
                "    def additional_args(self):\n",
                "        return BastankhahGaussianDeficit.additional_args.fget(self) | self._additional_args\n",
                "\n",
                "    def calc_deficit(self, WS_ilk, WS_eff_ilk, D_src_il, dw_ijlk, cw_ijlk, ct_ilk, **kwargs):\n",
                "        return BastankhahGaussianDeficit.calc_deficit(self, D_src_il, dw_ijlk, cw_ijlk, ct_ilk,\n",
                "                                                      WS_ilk=WS_ilk, WS_eff_ilk=WS_eff_ilk, **kwargs)\n",
                "\n",
                "    def get_ddeficit_dx(self, argnum):\n",
                "        import numpy as np  # override autograd.numpy\n",
                "        from numpy import newaxis as na\n",
                "\n",
                "        def ddeficit_dx(ans, WS_ilk, WS_eff_ilk, D_src_il, dw_ijlk, cw_ijlk, ct_ilk, **kwargs):\n",
                "            _, _, _, K = np.max([dw_ijlk.shape, cw_ijlk.shape, WS_ilk[:, na].shape], 0)\n",
                "            eps = 0\n",
                "            WS_ref_ilk = (WS_ilk, WS_eff_ilk)[self.use_effective_ws]\n",
                "            ky_ilk = self.k_ilk(**kwargs)\n",
                "            beta_ilk = 0.5 * (1 + 1 / np.sqrt(1 - ct_ilk))\n",
                "            sigma_ijlk = ky_ilk[:, na] * dw_ijlk * (dw_ijlk > eps) + \\\n",
                "                .2 * D_src_il[:, na, :, na] * np.sqrt(beta_ilk[:, na])\n",
                "            a_ijlk = ct_ilk[:, na] / (8. * (sigma_ijlk / D_src_il[:, na, :, na])**2)\n",
                "            sqrt_ijlk = np.sqrt(np.maximum(0., 1 - a_ijlk))\n",
                "            layout_factor_ijlk = WS_ref_ilk[:, na] * (dw_ijlk > eps) * np.exp(-0.5 * (cw_ijlk / sigma_ijlk)**2)\n",
                "            with warnings.catch_warnings():\n",
                "                warnings.simplefilter(\"ignore\")\n",
                "                if argnum == 0:\n",
                "                    dWS = ans / WS_ref_ilk[:, na]\n",
                "                elif argnum == 1:\n",
                "                    dWS_eff = ans / WS_eff_ilk[:, na]\n",
                "                elif argnum == 2:\n",
                "                    dD_sqrt_pos = (a_ijlk * (1 / D_src_il[:, na, :, na] - 0.2 * np.sqrt(beta_ilk[:, na]) / sigma_ijlk) / sqrt_ijlk +\n",
                "                                   (1 - sqrt_ijlk) * (cw_ijlk**2 / sigma_ijlk**3) * .2 * np.sqrt(beta_ilk[:, na])) * layout_factor_ijlk\n",
                "                    dD_sqrt_neg = (cw_ijlk**2 / sigma_ijlk**3) * .2 * np.sqrt(beta_ilk[:, na]) * layout_factor_ijlk\n",
                "                    dD = np.where(sqrt_ijlk == 0, dD_sqrt_neg, dD_sqrt_pos)\n",
                "                elif argnum == 3:\n",
                "                    ddw_sqrt_pos = (-a_ijlk / sqrt_ijlk + (1 - sqrt_ijlk) * (cw_ijlk / sigma_ijlk)**2) * \\\n",
                "                        ky_ilk[:, na] / sigma_ijlk * layout_factor_ijlk\n",
                "                    ddw_sqrt_neg = (cw_ijlk / sigma_ijlk)**2 * ky_ilk[:, na] / sigma_ijlk * layout_factor_ijlk\n",
                "                    ddw = np.where(sqrt_ijlk == 0, ddw_sqrt_neg, ddw_sqrt_pos)\n",
                "                elif argnum == 4:\n",
                "                    dcw = ans * (- cw_ijlk / (sigma_ijlk**2))\n",
                "                elif argnum == 5:\n",
                "                    dsigmadct_ilk = 0.2 * D_src_il[:, :, na] / (8 * np.sqrt(beta_ilk * (1 - ct_ilk)**3))\n",
                "                    dct_sqrt_pos = (a_ijlk * (1 / (2 * ct_ilk[:, na]) - dsigmadct_ilk[:, na] / sigma_ijlk) / sqrt_ijlk +\n",
                "                                    (1 - sqrt_ijlk) * (cw_ijlk**2 / sigma_ijlk**3) * dsigmadct_ilk[:, na]) * layout_factor_ijlk\n",
                "                    dct_sqrt_neg = (cw_ijlk**2 / sigma_ijlk**3) * dsigmadct_ilk[:, na] * layout_factor_ijlk\n",
                "                    dct = np.where(sqrt_ijlk == 0, dct_sqrt_neg, dct_sqrt_pos)\n",
                "\n",
                "            def dWS_ilk(g):\n",
                "                r = g * dWS[:g.shape[0], :g.shape[1], :g.shape[2], :g.shape[3]]\n",
                "                j = np.r_[np.where(g)[1], 0][0]\n",
                "                ilk = (slice(None), j)\n",
                "                return r[ilk]\n",
                "\n",
                "            def dWS_eff_ilk(g):\n",
                "                r = g * dWS_eff[:g.shape[0], :g.shape[1], :g.shape[2], :g.shape[3]]\n",
                "                j = np.r_[np.where(g)[1], 0][0]\n",
                "                ilk = (slice(None), j)\n",
                "                return r[ilk]\n",
                "\n",
                "            def dD_src_il(g):\n",
                "                r = g * dD[:g.shape[0], :g.shape[1], :g.shape[2], :g.shape[3]]\n",
                "                j = np.r_[np.where(g)[1], 0][0]\n",
                "                k = np.r_[np.where(g)[3], 0][0]\n",
                "                il = (slice(None), j, slice(None), k)\n",
                "                return r[il]\n",
                "\n",
                "            def ddw_ijlk(g):\n",
                "                r = g * ddw[:g.shape[0], :g.shape[1], :g.shape[2], :g.shape[3]]\n",
                "                if dw_ijlk.shape[-1] == 1 and K > 1:\n",
                "                    # If dw_ijlk is independent of ws, i.e. last dimension is 1 while len(ws)>1\n",
                "                    # then we need to sum the gradients wrt. wind speeds\n",
                "                    r = r.sum(3)[:, :, :, na]\n",
                "                return r[:, :, :, 0:dw_ijlk.shape[3]]\n",
                "\n",
                "            def dcw_ijlk(g):\n",
                "                r = g * dcw[:g.shape[0], :g.shape[1], :g.shape[2], :g.shape[3]]\n",
                "                if cw_ijlk.shape[-1] == 1 and K > 1:\n",
                "                    # If cw_ijlk is independent of ws, i.e. last dimension is 1 while len(ws)>1\n",
                "                    # then we need to sum the gradients wrt. wind speeds\n",
                "                    r = r.sum(3)[:, :, :, na]\n",
                "                return r[:, :, :, 0:cw_ijlk.shape[3]]\n",
                "\n",
                "            def dct_ilk(g):\n",
                "                r = g * dct[:g.shape[0], :g.shape[1], :g.shape[2], :g.shape[3]]\n",
                "                j = np.r_[np.where(g)[1], 0][0]\n",
                "                ilk = (slice(None), j)\n",
                "                return r[ilk]\n",
                "\n",
                "            return [dWS_ilk, dWS_eff_ilk, dD_src_il, ddw_ijlk, dcw_ijlk, dct_ilk][argnum]\n",
                "        return ddeficit_dx\n"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "b3e2220c",
            "metadata": {},
            "source": [
                "In this example, however, the model with manual gradient functions performs worse than the original where autograd derives the gradient functions automatically."
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 21,
            "id": "c3c84e8a",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "Time, automatic gradients 0.4170392\n",
                        "Time, manual gradients 0.4839589\n"
                    ]
                }
            ],
            "source": [
                "from py_wake.wind_farm_models import PropagateDownwind\n",
                "from py_wake.examples.data.hornsrev1 import wt16_x, wt16_y\n",
                "\n",
                "wfm_autograd = PropagateDownwind(site, wt, BastankhahGaussianDeficit())\n",
                "wfm_manual = PropagateDownwind(site, wt, BastankhahGaussianDeficitGradients())\n",
                "\n",
                "ws = np.arange(4,26)\n",
                "x,y = wt16_x, wt16_y\n",
                "ref, t_auto = timeit(lambda: wfm_autograd.aep_gradients(gradient_method=autograd, wrt_arg=['x','y'])(x, y, ws=ws))()\n",
                "res, t_manual = timeit(lambda: wfm_manual.aep_gradients(gradient_method=autograd, wrt_arg=['x','y'])(x, y, ws=ws))()\n",
                "np.testing.assert_array_almost_equal(res, ref, 4)\n",
                "\n",
                "print (\"Time, automatic gradients\", np.mean(t_auto))\n",
                "print (\"Time, manual gradients\", np.mean(t_manual))"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "ec141aea",
            "metadata": {},
            "source": [
                "### Comparison - Scalability of AEP gradients\n",
                "\n",
                "As seen in the previous comparison of scalability example, the autograd scales much better with the number of input variables than finite difference and complex step. \n",
                "\n",
                "When considering large wind farms, autograd is convincingly outperforming both finite difference and complex step, but it also requires much more memory.\n",
                "\n",
                "**The following plots are based on simulation performance on the Sophia HPC cluster.**"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 22,
            "id": "12100684",
            "metadata": {},
            "outputs": [
                {
                    "data": {
                        "text/plain": [
                            "'c:\\\\mmpe\\\\programming\\\\python\\\\Topfarm\\\\PyWake\\\\docs\\\\notebooks'"
                        ]
                    },
                    "execution_count": 22,
                    "metadata": {},
                    "output_type": "execute_result"
                },
                {
                    "data": {
                        "image/png": "iVBORw0KGgoAAAANSUhEUgAAA+UAAAFzCAYAAABYY6j9AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/NK7nSAAAACXBIWXMAAA9hAAAPYQGoP6dpAAChgElEQVR4nOzdeVxU9f7H8dcMy7AruAAqLihq7pplaamVkGXbrWyxW1ldr2mbmVlmJXVN08qsbLNbZovZ/rtmZlK5pLa4pJb7viMqKDvMcn5/jIwSLoDAmYH38/HgwcyZM+e8+TIH5jPf7/kei2EYBiIiIiIiIiJS5axmBxARERERERGpqVSUi4iIiIiIiJhERbmIiIiIiIiISVSUi4iIiIiIiJhERbmIiIiIiIiISVSUi4iIiIiIiJhERbmIiIiIiIiISVSUi4iIiIiIiJjE3+wAlc3lcrFv3z7Cw8OxWCxmxxEREcEwDLKysmjQoAFWqz4fP1v6Xy8iIt6mLP/rq31Rvm/fPuLi4syOISIiUsLu3btp1KiR2TF8nv7Xi4iItyrN//pqX5SHh4cD7saIiIg47bp2u5158+aRlJREQEBAVcSrNtR25aN2Kz+1Xfmo3cqvItsuMzOTuLg4z/8oOTtl+V8POg7KS+1Wfmq78lG7lY/arfzM+l9f7YvyomFsERERpSrKQ0JCiIiI0Au4jNR25aN2Kz+1Xfmo3cqvMtpOQ60rRln+14OOg/JSu5Wf2q581G7lo3YrP7P+1+tENhEREak0ycnJWCyWYl8xMTGexw3DIDk5mQYNGhAcHEzv3r1Zu3atiYlFRESqlopyERERqVRt27Zl//79nq8///zT89jEiROZNGkSU6ZMYdmyZcTExJCYmEhWVpaJiUVERKqOinIRERGpVP7+/sTExHi+6tWrB7h7ySdPnszo0aO5/vrradeuHdOnTyc3N5cZM2aYnFpERKRqVPtzykVEfJVhGDgcDpxOZ4Vt02634+/vT35+foVutyYoS9v5+fnh7++vc8aP2bx5Mw0aNMBms9GtWzfGjRtHfHw827dvJzU1laSkJM+6NpuNXr16sXTpUgYPHnzS7RUUFFBQUOC5n5mZCbh/R3a7/aTPMQwDp9OJ0+n0/C6zs7Px99dbodJyOBxV3m4WiwU/Pz/8/Px8+ngqel2e6vUpJ6d2Kx+1W/lVZNuVZRv6TyQi4oUKCwvZv38/ubm5FbpdwzCIiYlh9+7dPv0G1wxlbbuQkBBiY2MJDAysgnTeq1u3bnzwwQe0bNmSAwcOMHbsWLp3787atWtJTU0FIDo6uthzoqOj2blz5ym3OX78eJ555pkSy+fNm0dISEiJ5Varldq1axMcHOz53cXExLBt27az+dFqJDPazTAMcnNzOXr0KC6Xq0r3XdFSUlLMjuCT1G7lo3Yrv4pou7K8h1NRLiLiZVwuF9u3b8fPz48GDRoQGBhYYQW0y+UiOzubsLAwrFadwVQWpW07wzAoLCzk4MGDbN++nYSEhBrd1ldccYXndvv27bnwwgtp3rw506dP54ILLgBKzkxrGMZpX/OjRo1i+PDhnvtFl51JSkoqMfv6icdTvXr1PLPp5uTkEBoaqg+nysAwjCpvN8MwsNvtHDx4kPr169OsWTOfPJ7sdjspKSkkJiZqNuwyULuVj9qt/Cqy7YpGcZWGinIRES9TWFiIy+UiLi7upL1+Z8PlclFYWEhQUJBPvrE1U1naLjg4mICAAHbu3Ol5jriFhobSvn17Nm/ezHXXXQdAamoqsbGxnnXS0tJK9J6fyGazYbPZSiwPCAgo8SYqPz8fwzBo2LCh53hyuVzY7XaCg4N1HJSBme0WGBjIzp07MQzDp4uMk71G5czUbuWjdiu/imi7sjxf/4lERLyUigXfpt/fyRUUFLB+/XpiY2Np1qwZMTExxYYJFhYWsnDhQrp3716h+9Xvw7fp9yci1Zl6ykVERKTSjBgxgquvvprGjRuTlpbG2LFjyczM5M4778RisTBs2DDGjRtHQkICCQkJjBs3jpCQEAYMGGB2dBERkSqholxETu7AWkj9CxISISTK7DQi4qP27NnDrbfeyqFDh6hXrx4XXHABv/76K02aNAFg5MiR5OXlMXToUDIyMujWrRvz5s0jPDzc5OQiIlLTfLzhYwynUeX71VggETm5VTPg63/D96PNTiI+xDAM/v3vfxMVFYXFYmHVqlUl1unduzfDhg2r8mxijpkzZ7Jv3z4KCwvZu3cvX375JW3atPE8brFYSE5OZv/+/eTn57Nw4ULatWtnYmLvoeNJRKTqpOxM4aWVL/FG9htk5GdU6b7VUy4iJRkGbPjWfbvVFadfV+QEc+fO5f3332fBggXEx8dTt25dsyOJ+CwdTyIiVWNP1h7GLBkDwHmB5xEZFFml+1dRLiIlHdoEGdvBLxCaX2p2GvEhW7duJTY2tsIn6RKpiXQ8iYhUPrvLzmOLHiPLnkWHuh3oY+9T5RlUlItISRvnuL836wW2MHOzCOAexppnd571dlwuF3mFTvwLHaWezTg4wK9U1yQeOHAg06dPB9xDkps0acLatWsZMmQIX331FeHh4YwYMeKs8otUBMMwynwcVBQdTyIi3uW1la+x5tAawgPDGddjHKsWrqryDCrKRaSkjd+5v7fqa24O8cizO2nz9Pem7Hvds5cTEnjmfxevvPIKzZs3Z+rUqSxbtgw/Pz8effRR5s+fz9dff01MTAxPPPEEK1asoFOnTpUfXOQU8uxOLpz0qyn71vEkIuI9ft7zM9PWTgPg2e7P0iC0AatYVeU5VJSLSHHZB2H37+7bLXU+uZRerVq1CA8Px8/Pj5iYGLKzs3n33Xf54IMPSExMBGD69Ok0atTI5KQi3k/Hk4hI5TqQc4DRi90TGt/S6hb6NOmD3W43JYuKchEpbvM8wIDYjlCrodlp5JjgAD/WPXv5WW/H5XKRlZlFeER4mYavl8fWrVspLCzkwgsv9CyLioqiVatW5dqeSEUJDvDjl+EXlOk4qMh9l4eOJxGRiuN0ORm1eBQZBRm0jmrNiPPMPR1IRbmIFFd0PnmrK83NIcVYLJZSDXk9E5fLhSPQj5BA/0ovRgyj6q/zKVIaFouF4Co6DiqKjicRkYozdc1UlqUuI9g/mBd6voDNz2ZqHt/4TyQiVcOeD1t/ct/WpdDkLLVo0YKAgAB+/fX4ubsZGRls2rTJxFQivknHk4hIxViWuoy31rwFwFMXPEXTWk3NDYR6ykXkRNsXgT0XIhpCTAez04iPCwsL45577uHRRx+lTp06REdHM3r0aJ/pmRTxJjqeRETOXnp+Oo8vehyX4eLa5tdydfOrzY4EqCgXkRMVDV1v2RdKcckekTN54YUXyM7O5pprriE8PJxHHnmEo0ePmh1LxCfpeBIRKT+X4WL04tGk5aXRrFYznuj2hNmRPFSUi4ibYcCmue7bOp9cymnYsGEMGzbMcz8sLIwPP/yQDz/80LPs0UcfNSGZiO/R8SQiUnE+WPsBi/cuxuZn48VeLxISEGJ2JA+NeRIRt/2rIGs/BIZBs4vNTiMiIiIiUiHWHFzDKytfAWDkeSNpGdnS5ETFqSgXEbeN37m/N78U/M2dgVJEREREpCJkFmYyctFIHIaDpCZJ9G/Z3+xIJagoFxE3XQpNRERERKoRwzBIXprM3uy9NAxrSHL3ZCxeOG+SinIRgSO7IfVPsFghIcnsNCIiIiIiZ+2zjZ+RsjMFf6s/L/Z6kfDAcLMjnZSKchE5PsFbXDcIrWNuFhERERGRs7QxfSMTl00EYFiXYbSr287kRKemolxEThi6foW5OUREREREzlKuPZcRC0dQ6CqkZ6Oe3NHmDrMjnZaKcpGaLj8Ttv/svq3zyUVERETExz3323PsyNxB/ZD6jO0x1ivPIz+RinKRmm7rT+CyQ50WUDfB7DQiIiIiIuU2a+ssZm2dhdViZcLFE4gMijQ70hmpKBep6Youhaah6yIiIiLiw7Yf3c7YX8cCMKTjELrGdDU5UemoKBepyZwO2Py9+7aGrouIiIiIjypwFjBi4QjyHHl0i+nGoPaDzI5Uav5mBxARE+3+DfIyIDgSGp1vdppSsztd/G/1flxOs5OIiIiIiDd4YdkLbMrYRFRQFOMvHo+f1c/sSKWmnnKRmqxo1vWEy8HPdz6jm78hjRFf/MkLa/wwDMPsOPI3LpeLCRMm0KJFC2w2G40bN+a5556jsLCQ+++/n9jYWIKCgmjatCnjx483O66I19KxJCJSOik7U/h046cAPHfRc9QLqWdyorLxnXfhIlLxiq5P7mPnk3+2fDcA7aMMr59Ns8IYBthzz347Lpd7O4V+YC3l57IBIVCGdh41ahTvvPMOL7/8MhdddBH79+9nw4YNvPrqq8yaNYvPPvuMxo0bs3v3bnbv3l3OH0TkLBQdT2U5DipKGY4nHUsiIme2J2sPY5aMAeDudndzUcOLTE5UdqYW5Q6Hg+TkZD7++GNSU1OJjY1l4MCBPPnkk1iP/ZM0DINnnnmGqVOnkpGRQbdu3Xj99ddp27atmdFFfN+hzXB4C/gFQovLzE5TammZ+czfeBCAC+q7TE5They5MK7BWW/GCtQu65Oe2AeBoaVaNSsri1deeYUpU6Zw5513AtC8eXMuuugiHnzwQRISErjooouwWCw0adKkrElEKoY9l9qvn2POvkt5POlYEhE5M7vLzmOLHiPLnkXHeh25v/P9ZkcqF1OHr0+YMIG33nqLKVOmsH79eiZOnMgLL7zAa6+95lln4sSJTJo0iSlTprBs2TJiYmJITEwkKyvLxOQi1UDR0PWmF4Mt3NwsZfDlyr04XQZdGtcmOtjsNPJ369evp6CggMsuK/lBz8CBA1m1ahWtWrXiwQcfZN68eSYkFPENOpZERM7stZWvsebQGsIDw5nYcyIB1gCzI5WLqT3lv/zyC9deey39+vUDoGnTpnzyyScsX74ccPeST548mdGjR3P99dcDMH36dKKjo5kxYwaDBw82LbuIz/PBS6EZhsHnx4au39ilARw4ZHKiKhQQ4u5hO0sul4vMrCwiwsM9I5JKte9SCg4+9SclXbp0Yfv27Xz33Xf88MMP3HTTTfTp04cvvvii1NsXqRABIRy5b33ZjoMK3Hdp6FgSETm9n/f8zLS10wB4tvuzNAg7+xGFZjG1KL/ooot466232LRpEy1btmT16tUsXryYyZMnA7B9+3ZSU1NJSkryPMdms9GrVy+WLl160qK8oKCAgoICz/3MzEwA7HY7drv9tHmKHj/TelKS2q58TGu3nEP47/4NC2CP7wM+8ntbvjODbYdyCAn0I7FVHZYeqJ6vObvdjmEYuFwuXK4Thuj7n/3QAMMwIMCJERCCq7TniRuG+6sUmjdvTnBwMCkpKfzrX/8q8XhYWBj9+/enf//+XH/99Vx55ZUcOnSIqKiosvwYpiiaVLDod3MmLpcLwzCw2+34+RWfAbY6vm59isXiLo4DQ6v+nPJSSkhIIDg4mB9//PGkx1JERAQ333wzN998MzfeeCN9+/YlPT3dJ44lEZGzdSDnAKMXjwbg1ta30qdJH5MTnR1Ti/LHHnuMo0eP0rp1a/z8/HA6nTz33HPceuutAKSmpgIQHR1d7HnR0dHs3LnzpNscP348zzzzTInl8+bNIySkdJ9Op6SklOXHkBOo7cqnqtst7vDPdDFcHAluzMIla4A1Vbr/8pqxxQpYaV/LztJF84Hq+Zrz9/cnJiaG7OxsCgsLK2UflXkK0EMPPcRjjz2Gy+WiW7duHDp0iA0bNpCVlUV0dDTt27fHarXyySefEB0djdVq9XyA6gtK23aFhYXk5eWxaNEiHA5Hscdycytg0j6p1oKCgnjssccYOXIkgYGB9OjRg4MHD7J27VoyMzOJjY2lU6dOWK1WPv/8c2JiYqhdu7bZsUVEKp3T5WTU4lFkFGTQOqo1j3R9xOxIZ83UovzTTz/lo48+YsaMGbRt25ZVq1YxbNgwGjRo4JnUBCgxu7JhnHrG5VGjRjF8+HDP/czMTOLi4khKSiIiIuK0eex2OykpKSQmJhIQ4JvnI5hFbVc+ZrWb35efAxB+7k1c2evKKtvv2cgucDBqxULAycPXdqNDg7Bq+5rLz89n9+7dhIWFERQUVKHbNgyDrKwswsPDK23m+v/85z+Ehoby/PPPs2/fPmJjYxk8eDB16tRhypQpbN68GT8/P8477zy+/fZbnykkytp2+fn5BAcH07NnzxK/R1/6EELM89RTT+Hv78/TTz/tOZbuvfde6taty4QJE4odS3PmzKn6ofgiIiaYumYqy1KXEewfzAs9X8DmZzM70lkztSh/9NFHefzxx7nlllsAaN++PTt37mT8+PHceeedxMTEAHhmZi+SlpZWove8iM1mw2Yr+YsJCAgo9Rv3sqwrxantyqdK282eD1t/AsCvzVX4+cjva96q/eQWOomvF0q35vU8PY/V8TXndDqxWCxYrdYKf5NdNOy6aPuVwWq18uSTT/Lkk0+WeMyX5wIpa9tZrVYsFstJX6PV7TUrlcNqtTJ69GhGjx5d4rFBgwaZkEhExFzLUpfx1pq3AHjqgqdoWqupuYEqiKkfqebm5pZ4Y+Pn5+d549OsWTNiYmKKDU8tLCxk4cKFdO/evUqzilQbOxaDPQfCYyG2k9lpSu2z5XsAuKlrXM25NrmIiIiIAJCen85jix7DZbi4tvm1XN38arMjVRhTe8qvvvpqnnvuORo3bkzbtm35448/mDRpEnfffTfg7o0YNmwY48aNIyEhgYSEBMaNG0dISAgDBgwwM7qI7yq6FFrLvu7JjnzAlrQsVuzMwM9q4frODc2OIyIiIiJVyGW4GL14NAfzDtKsVjOe6PaE2ZEqlKlF+WuvvcZTTz3F0KFDSUtLo0GDBgwePJinn37as87IkSPJy8tj6NChZGRk0K1bN+bNm0d4uO9cV1nEaxjGCZdC841zyQE+P9ZLfkmretSPqNhzrEVERETEu32w9gMW712Mzc/Gi71eJKQMl2v1BaYW5eHh4UyePNlzCbSTsVgsJCcnk5ycXGW5RKqt/asha5/7UkDNepqdplTsThdfrjw+dF1EREREao41B9fwyspXABh53khaRrY0OVHF0zSdIjXJprnu780vhQDf6HGevyGNQ9mF1A2zcUnr+mbHEREREZEqklmYychFI3EYDpKaJNG/ZX+zI1UKFeUiNUnR+eQ+NHT9s+W7AbihS0MC/PQnS0RERKQmMAyD5KXJ7M3eS8OwhiR3T662k/3qHa5ITXF0r3v4OhZoebnZaUolLTOf+RsPAtBfQ9dFREREaozPNn5Gys4U/K3+vNjrRcIDq++cYirKRWqKTccmeIs7H0LrmpullL76Yy9Ol8G5TSJpUT/M7DgiIiIiUgU2pm9k4rKJAAzrMox2dduZnKhyqSgXqSk8s65fYW6OUjIMg8+WuYeu39S1kclpRERERKQq5NpzGbFwBIWuQno26skdbe4wO1KlU1EuUhMUZMH2Re7bPnI++YqdGWw7lENIoB/9OjQwO45ICTt27MBisbBq1Sqzo4j4PB1PIlLkud+eY0fmDuqH1Gdsj7HV9jzyE6koF6kJts4HZyFExUNd37iMxKfHesn7tY8lzGbq1Rulir3//vvUrl3b7Bgi1YKOJxHxJbO2zmLW1llYLVYmXDyByKBIsyNVCRXlIjWBZ+j6leADnzZmFzj49s/9ANx8niZ4k8pjt9vNjiBSbeh4EpGzsf3odsb+OhaAIR2H0DWmq8mJqo6KcpHqzuU8fn3yln3NzVJK367ZR26hk/i6oZzbpGZ8QlqdzJ07l4suuojatWtTp04drrrqKrZu3QrAggULsFgsHDlyxLP+qlWrsFgs7NixgwULFnDXXXdx9OhRLBYLFouF5ORkADIyMrjjjjuIjIwkJCSEK664gs2bNxfb9zvvvENcXBwhISH84x//YNKkScV6CZOTk+nUqRPvvfce8fHx2Gw2DMM4beYiv//+Oz179iQkJISuXbvyxx9/VEr7iZzIm46nl19+mSZNmngeP9vjqXPnzgQFBel4EhHyHfmMWDiCPEce3WK6Maj9ILMjVSkV5SLV3e7fIS8dgmpD4wvMTlMqny3fA7gvg1YTziMqDcMwyLXnVshXniOvTOsbhlGmrDk5OQwfPpxly5bx448/YrVa+cc//oHL5Trjc7t3787kyZOJiIhg//797N+/nxEjRgAwcOBAli9fzqxZs/jll18wDIMrr7zS0zu3ZMkS7r33Xh566CFWrVpFYmIizz33XIl9bNmyhc8++4wvv/zSc/7qmTLn5ORwzTXX0KJFC5YtW0ZycrInl/gewzDKfBxU1JcvH0/jxo0rsY/yHk9XXXUVrVq1YsWKFTqeRIQXl7/IpoxNRAVFMf7i8fhZ/cyOVKV0oqZIdbdxjvt7QhL4BZibpRS2pGWxYmcGflYLN3RpaHYcr5HnyKPbjG6m7Pu3Ab8REhBS6vVvuOGGYvffffdd6tevz7p168743MDAQGrVqoXFYiEmJsazfPPmzcyaNYslS5bQvXt3AD7++GPi4uL4v//7P/r3789rr73GFVdc4Xlz37JlS5YuXcrs2bOL7aOwsJAPP/yQevXqlSpzu3bt+Pjjj3E6nUyZMoWYmBjat2/Pnj17GDJkSKnbRbxHniOPpG+TTNm3Lx9PS5YsqdDj6b333iMkJIS2bdvqeBKpwVJ2pvDpxk8BGHfROOqF1DvDM6of9ZSLVHc+dim0z4/1kl/Sqh71I4JMTiPlsXXrVgYMGEB8fDwRERE0a9YMgF27dpV7m+vXr8ff359u3Y5/MFGnTh1atWrF+vXrAdi4cSPnn39+sef9/T5AkyZNihUQpcm8fv16OnbsSEjI8WLqwgsvLPfPU5ONHz8ei8XCsGHDPMsMwyA5OZkGDRoQHBxM7969Wbt2rXkhvYiOJxGpzvZk7WHMkjEA3N3ubno07GFyInOop1ykOju0BQ5vBmsAtLjM7DRnZHe6+HLlXgBu6qoJ3k4U7B/MbwN+O+vtuFwusrKyCA8Px2ot3eeywf7BZdrH1VdfTVxcHO+88w4NGjTA5XLRrl07CgsLCQsLAyg2hLc0k0OdasivYRieUxxOvH2654WGhpYp8+n2L2WzbNkypk6dSocOHYotnzhxIpMmTeL999+nZcuWjB07lsTERDZu3Eh4eHiF5wj2D2Zev3llOg4qct9loeNJRKoru8vOY4seI8ueRcd6Hbm/8/1mRzKNinKR6mzTsV7yphdBUC1zs5TC/A1pHMouoG6YjUta1zc7jlexWCxlGvJ6Ki6XC4e/g5CAkEopRg4fPsz69et5++23ufjiiwFYvHix5/GiHrX9+/cTGemexO/v1yUODAzE6XQWW9amTRscDge//fabZ7jt4cOH2bRpE+eccw4ArVu35vfffy/2vOXLl5915qL9f/jhh+Tl5REREQHAr7/+esZty3HZ2dncdtttvPPOO4wdO9az3DAMJk+ezOjRo7n++usBmD59OtHR0cyYMYPBgwdXeBaLxUKwf3ClHQcVpSYcT8HB7g8pdDyJ1DyvrXyNNYfWEB4YzsSeEwmwev9plpXFe/8TicjZ87Gh60UTvN3QpSEBfvrz5IsiIyOpU6cOU6dOZcuWLfz0008MHz7c83iLFi2Ii4sjOTmZTZs28e233/LSSy8V20bTpk3Jzs7mxx9/5NChQ+Tm5pKQkMC1117LoEGDWLx4MatXr+af//wnDRs25NprrwXggQceYM6cOUyaNInNmzfz9ttv8913351xssAzZQYYMGAAVquVBx54gHXr1jFnzhxefPHFCmq1muG+++6jX79+9OnTp9jy7du3k5qaSlLS8XO8bTYbvXr1YunSpVUd06t42/E0d+7cCj2e7rnnHh1PIjXUz3t+ZtraaQA82/1ZGoQ1MDmRudRTLlJd5abDrl/ct33gUmhpmfnM35gGuGddF99ktVqZOXMmDz74IO3ataNVq1a8+uqr9O7dG4CAgAA++eQThgwZQseOHTnvvPMYO3Ys/fv392yje/fu3Hvvvdx8880cPnyYMWPGkJyczLRp03jooYe46qqrKCwspGfPnsyZM4eAAPcn6z169OCtt97imWee4cknn+Tyyy/n4YcfZsqUKWeVGSAsLIz//e9/DB48mHPPPZc2bdowYcKEEhNaycnNnDmTlStXsmzZshKPpaamAhAdHV1seXR0NDt37jzp9goKCigoKPDcz8zMBNxDt/8+fNtut2MYBi6XyzP7d9Hw6aLl3mzGjBkMGzbM89qcPHkyl156KS6XCz8/Pz7++GPuu+8+z/H07LPPcvPNN3t+3gsuuIDBgwd7jqenn36aMWPG8O677zJs2DDP8XTxxRcze/Zs/Pz8cLlcXHjhhbzxxhv85z//4cknnyQpKYmHHnqI119/3dNuRe349zY8XWaXy0VISAj/+9//GDp0KJ07d6ZNmzaMHz+e/v37F/s9nahof3a7HT8/35uVueh1qWu5l43arXy8vd3SctN4YvETANzc8mZ6NejlNVkrsu3Ksg2LUc1P7MnMzKRWrVocPXrUM+TwVOx2O3PmzOHKK6/0vMmT0lHblU+lttvqmfD1YIhuB0OWVOy2K8FbC7fy/HcbOLdJJF8O6X7G9avzay4/P5/t27fTrFkzgoIqdrI7l8tFZmYmERERXj1st6IMGjSIDRs28PPPP5/1tsradqf7PZblf5Ov2717N127dmXevHl07NgRgN69e9OpUycmT57M0qVL6dGjB/v27SM2NtbzvEGDBrF7927mzp1bYpvJyck888wzJZbPmDGj2ORhAP7+/sTExBAXF0dgYGAF/3Q1y0MPPcSmTZv47rvvqnzfhYWF7N69m9TUVBwOR5XvX0QqhstwMS1nGtsd24n1i+XfYf8mwFK93scVyc3NZcCAAaX6X6+ecpHqquhSaD4wdN0wDD5bthuAm7o2MjmN+LIXX3yRxMREQkND+e6775g+fTpvvPGG2bFqtBUrVpCWlsa5557rWeZ0Olm0aBFTpkxh48aNgLvH/MSiPC0trUTveZFRo0YVGxKdmZlJXFwcSUlJJd745Ofns3v3bsLCwjwfjhiG4Znw8EzDsWuyl156iT59+hAaGsrcuXP55JNPePHFF01pt/z8fIKDg+nZs2eFf1hZFex2OykpKSQmJla7D5Irk9qtfLy53V5d9Srb120n2D+YN/q+QZOIJmZHKqYi265oFFdpqCgXqY4cBbDlJ/dtHyjKV+zMYNuhHEIC/ejXoWafUyRn5/fff2fixIlkZWURHx/Pq6++yr/+9S+zY9Vol112GX/++WexZXfddRetW7fmscceIz4+npiYGFJSUujcuTPg7hVduHAhEyZMOOk2bTYbNputxPKAgIASb6KcTicWiwWr1eoZ4VA0PLpouZzcsmXLeOGFFzzH0+TJkxkwYIAp7Wa1WrFYLCf9HfsSX89vFrVb+Xhbu32z9RveX/c+AMkXJtOiTgtzA51GRbRdWZ6volykOtqxGAqzICwGYjubneaMPlvu7iXv1z6WMJv+LEn5ffbZZ2ZHkL8JDw+nXbt2xZaFhoZSp04dz/Jhw4Yxbtw4EhISSEhIYNy4cYSEhDBgwAAzIssxfz+eik7hEBEpqzUH15C8NBmAf7X/F1fGX2luIC+jd78i1VHRrOstLwcv7wXKLnAwe81+AG46TxO8idREI0eOJC8vj6FDh5KRkUG3bt2YN29epVyjXEREqtaBnAMMmz+MQlchveN680DnB8yO5HVUlItUN4ZxwqXQvP9TyDlr9pNb6CS+bihdm0SaHUdEqsCCBQuK3bdYLCQnJ5OcnGxKHhERqRx5jjwemv8QB/MO0qJ2C56/+HmsFu/uMDKDWkSkukn9EzL3gH8wxPcyO80ZfXps6Hr/rnGacOlvqvnFMao9/f68i34fvk2/PxHfYxgGY5aMYe3htdS21ea1S18jNCDU7FheSUW5SHVT1Eve/FIICDY3yxlsSctmxc4M/KwWbujS0Ow4XqNoYpDc3FyTk8jZKPr9edMkOzWRjqfqQceTiO955893+G7Hd/hb/JnUexKNwnWFnVPR8HWR6mZT0dB17591/fNjveSXtKpH/Qjfu8RNZfHz86N27dqkpaUBEBISUmGjCFwuF4WFheTn52vW6TIqbdsZhkFubi5paWnUrl0bPz+/Kkwpf3ey48kwDB0H5WDG3w8dTyK+6cedP/LaH68B8MQFT3BezHkmJ/JuKspFqpPMfbDvD8DinuTNi9mdLr5cuReAm7pqgre/i4mJAfAUEhXFMAzy8vIIDg7W6QJlVNa2q127tuf3KOb6+/Gk46B8zGw3HU8ivmNj+kZGLR4FwK2tb6V/y/4mJ/J+KspFqpNNc93fG3WFsPrmZjmD+RvSOJRdQN2wQC5p7d1ZzWCxWIiNjaV+/frY7fYK267dbmfRokX07NlTw0DLqCxtFxAQoB49L/L340nHQfmY1W46nkR8x+G8wzz404PkOfLoFtuNkeeNNDuST1BRLlKdbPSdoeufLd8DwPVdGhHgp+Gjp+Ln51ehb0b9/PxwOBwEBQWpGCkjtZ3vKzqe9LssH7WbiJyO3Wln+ILh7MvZR+PwxrzU6yX8rSo3S0PvhEWqi4Js2LbQfdvLL4WWlpXP/I3uYaQ3ddWkHyIiIiK+zDAMxv42lpVpKwkLCOO1y16jlq2W2bF8hopykepi23xwFkBkU6jX2uw0p/XVyr04XQZdGtemRf1ws+OIiIiIyFn4eP3HfLX5K6wWKxN7TiS+VrzZkXyKinKR6mLjsfPJW10JXjxxkWEYfHZs1vWbz9MEbyIiIiK+bOnepbyw/AUAhp87nIsbXWxyIt+jolykOnA5j0/y1rKvuVnOYMXODLYdzCEk0I9+HRqYHUdEREREymnH0R2MWDQCl+Hi2ubXckebO8yO5JNUlItUB3uWQ+4hsNWCJt3NTnNaRb3k/drHEmbT5B8iIiIivuhowVEe+OkBsgqz6FSvE09f+LQuM1lOKspFqoONc9zfExLBz3tnxM0ucDB7zX4AbtLQdRERERGf5HA5GLloJDsydxATGsPLl7xMoF+g2bF8lopykerARy6FNmfNfnILncTXDaVrk0iz44iIiIhIOby0/CWW7ltKsH8wr17yKnWD65odyaepKBfxdYe3wqGNYPWHFn3MTnNaRUPX+3eN0/AmERERER/09eav+Wj9RwCM7TGWc+qcY3Ii36eiXMTXFU3w1qQHBNc2NcrpbEnLZvnODPysFm7o0tDsOCIiIiJSRisPrOTZX58FYGjHoSQ1TTI5UfWgWZZEfJ2PDF3/fIW7l/ySVvWoHxFkchoR+btZs2aV+TmJiYkEBwdXQhoREfE2+7L38fCCh3G4HCQ2SWRwx8FmR6o2VJSL+LLcdNi51H3biy+FZne6+HLFXsA9dF1EvM91111XpvUtFgubN28mPj6+cgKJiIjXyLXn8sBPD5Cen845UecwtsdYrBYNuq4oakkRX7blBzCcUL8NRDUzO80pLdh4kEPZBdQNC+TS1vXNjiMip5CamorL5SrVV0hIiNlxRUSkCrgMF08sfoJNGZuoE1SHVy99lZAA/Q+oSCrKRXxZ0aXQvHzo+qfL3EPXr+/SiAA//dkR8UZ33nlnmYai//Of/yQiIqISE4mIiDd4Y9Ub/LjrRwKsAUy+ZDIxoTFmR6p2NHxdxFc5CmHzD+7bra40N8tppGXlM39jGgA3dW1kchoROZVp06aVaf0333yzkpKIiIi3mLt9Lm+veRuAMReOoVP9TuYGqqbUZSXiq3YugcIsCK0PDbqYneaUvl65F6fLoEvj2rSoH252HBEREREphbWH1/LkkicBGNh2INe2uNbkRNWXinIRX1U063rLy8HqnYeyYRh8euza5DefpwneRHzB/Pnzeemll1iyZAkAb7/9No0bN6ZevXoMGjSIvLw8kxOKiEhlO5h7kAd/epACZwEXN7yYYV2GmR2pWtPwdRFfZBgnXArNe4eur9yVwbaDOQQH+NGvQwOz44jIGbzzzjsMGTKEpk2bMnr0aMaMGcNzzz3H7bffjtVq5aOPPqJOnTo8//zzZkcVEZFKUuAsYNj8YaTlphFfK54JPSfgZ/UzO1a15p3dayJyegfWwtFd4B8E8b3NTnNKRRO89esQS5hNnwGKeLtXXnmFl19+mS1btvB///d/PP3007z++uu8+eabvP766/z3v//liy++MDumiIhUEsMwSF6azJpDa4gIjOC1S18jPFCnH1Y2FeUivqiolzz+Egj0zktS5BQ4mL1mP6Ch6yK+Ytu2bVxzzTUA9O3bF4vFwvnnn+95vFu3buzevduseCIiUsmmrZ3G7G2z8bP48VLvl2gc0djsSDWCinIRX+QDl0L7ds1+cgudxNcNpWuTSLPjiEgp5OfnF7ssms1mw2azFbvvcDjMiCYiIpVs4e6FTF4xGYDHzn+MC2IvMDdQDaLxpCK+JisV9q103255ublZTuOzYxO89e8ah8ViMTmNiJSGxWIhKyuLoKAgDMPAYrGQnZ1NZmYmgOe7iIhUL1sytvDYz49hYNC/ZX9uaXWL2ZFqFBXlIr5m01z394bnQniMuVlOYUtaNst3ZuBntXBDl4ZmxxGRUjIMg5YtWxa737lz52L39SGbiEj1ciT/CA/89AA59hy6RndlVLdR+ltfxVSUi/gaz6zr3jt0/fMV7l7yS1rVo35EkMlpRKS05s+fb3YEERGpQnaXneELh7Mnew8NwxoyqfckAqwBZseqcVSUi/iSwhzYtsB920svhWZ3uvhyxV7APXRdRHxHr169zI4gIiJVaMLvE1iWuowQ/xCmXDqFyCDNA2QG0yd627t3L//85z+pU6cOISEhdOrUiRUrVngeNwyD5ORkGjRoQHBwML1792bt2rUmJhYx0bYF4MiH2o2hfhuz05zUgo0HOZRdQN2wQC5tXd/sOCJyFtauXcuaNWs8X/r/KyJSfczcMJNPN36KBQsTek6gRWQLsyPVWKYW5RkZGfTo0YOAgAC+++471q1bx0svvUTt2rU960ycOJFJkyYxZcoUli1bRkxMDImJiWRlZZkXXMQsnlnXrwQvPdenaIK367s0IsDP9M/9RKQMfv75Z8477zzP/QsuuIDOnTvTqVMnOnXqRIcOHfjhhx9MTCgiIhXht/2/8fzvzwPwYJcH6R3X29xANZypw9cnTJhAXFwc06ZN8yxr2rSp57ZhGEyePJnRo0dz/fXXAzB9+nSio6OZMWMGgwcPrurIIuZxuWDT9+7bLfuam+UU0rLy+WlDGgA3dW1kchoRKas33niD22+/vdiy+fPn06RJEwzD4NVXX+XNN9+kT58+JiUUEZGztTtzN48sfASn4aRffD/uaXeP2ZFqPFOL8lmzZnH55ZfTv39/Fi5cSMOGDRk6dCiDBg0CYPv27aSmppKUlOR5js1mo1evXixduvSkRXlBQQEFBQWe+0WXb7Hb7djt9tPmKXr8TOtJSWq78ilLu1n2Lsc/5yCGLRxHw/PBC9v6i+W7cLoMOsfVoklkUKW+HvSaKx+1W/lVZNt5a/svW7aMhx56qNiyRo0a0aRJEwBuv/12+vXrZ0Y0ERGpANmF2dz/0/0cLThK+7rteab7M5pp3QuYWpRv27aNN998k+HDh/PEE0/w+++/8+CDD2Kz2bjjjjtITU0FIDo6utjzoqOj2blz50m3OX78eJ555pkSy+fNm0dISEipcqWkpJTxJ5EiarvyKU27nbPvc1oCe4PbsOJ77xs+ahjw/io/wEKrgHTmzJlTJfvVa6581G7lVxFtl5ubWwFJKt7evXuJjY313J8+fToxMccvvRgVFcXhw4fNiCYiImfJ6XIyctFIth3dRv3g+rxyySvY/GxmxxJMLspdLhddu3Zl3LhxAHTu3Jm1a9fy5ptvcscdd3jW+/unN6e7TuqoUaMYPny4535mZiZxcXEkJSURERFx2jx2u52UlBQSExMJCNClAMpCbVc+ZWk3/6nu4ySm111c2c77Zl5fuesIab/+TnCAlccGXEqYrXL/vOg1Vz5qt/KryLYrGsXlbcLDw9m+fbunZ7zo1LEi27dvP+P/UhER8U6vrHyFn/f+jM3PxquXvkq9kHpmR5JjTC3KY2NjadOm+AzS55xzDl9++SWA59P51NTUYp/cp6Wlleg9L2Kz2bDZSn7iExAQUOo3UWVZV4pT25XPGdstfRsc3AAWP/xb9wUvbOOv/tgPQL8ODYgMC66y/eo1Vz5qt/KriLbz1rbv1q0bH3zwAb179z7p4++//z7dunWr2lAiInLWZm2dxbS17nm8xvYYS9u6bU1OJCcydWrkHj16sHHjxmLLNm3a5PmEvlmzZsTExBQbKlhYWMjChQvp3r17lWYVMdXGue7vTbpDsPddPzKnwMHsNfsAuPk8XZtcxFcNHz6c6dOn8+ijj5KWluZZnpaWxiOPPMJHH31UbDSaiIh4v9UHV5O8NBmAQe0H0beZd04YXJOZ2lP+8MMP0717d8aNG8dNN93E77//ztSpU5k6dSrgHrY+bNgwxo0bR0JCAgkJCYwbN46QkBAGDBhgZnSRqrXpO/f3VleYm+MUvv1zPzmFTuLrhtK1ifd9aCAipXPJJZfw2muv8fDDDzNp0iQiIiKwWCwcPXoUf39/Jk+ezKWXXmp2TBERKaXUnFQe+ukh7C47l8Zdyv2d7zc7kpyEqUX5eeedx9dff82oUaN49tlnadasGZMnT+a2227zrDNy5Ejy8vIYOnQoGRkZdOvWjXnz5hEeHm5icpEqlJcBO5a4b3tpUf7ZMve1yft3jdMMniI+bujQoVx99dV88cUXbN68GYCEhARuvPFG4uI0EkZExFfkOfJ48KcHOZx/mJaRLRl/8XisFlMHSsspmFqUA1x11VVcddVVp3zcYrGQnJxMcnJy1YUS8SZbfgTDCfVaQ1S82WlK2Howm+U7M/CzWrihS0Oz44hIBYiLi+Phhx82O4aIiJSTYRgk/5rM+vT1RNoiefXSVwkJKN2VqKTq6aMSEW+38dilxby1l3y5u5f8klb1qB8RZHIaESmvWbNmlen66XPmzCEvL68SE4mISHktKFhAyq4U/K3+vHzJyzQMU8eJN1NRLuLNHIWw+dg1yVt532XQ7E4XX67YC7iHrouI7/rHP/7BkSNHSr3+Lbfcwv79+ysvkIiIlMsPu37gx/wfAXiy25OcG32uyYnkTEwfvi4ip7FrKRQchZC60ND7/qAu2HiQQ9kF1A0L5NLW9c2OIyJnwTAMBg4ceNLLip5Mfn5+JScSEZGy+mXfL4xeOhqAW1veyg0tbzA5kZSGinIRb1Z0KbSWfcHqZ26Wkygaun59l0YE+GngjYgvu/POO8u0/m233UZEREQlpRERkbJafXA1D813z7TeNqAtw7voEpa+QkW5iLcyDK8+nzwtK5+fNrivY3xT10YmpxGRszVt2jSzI4iISDltytjEkB+GkOfI44KYC+ib1xc/L+zQkZNT15aIt0pbD0d2gp8Nml9idpoSvl65F6fLoEvj2rSor0sUioiIiJhhV+YuBqcMJqswi471OvJSz5fwt6jv1ZeU6rf16quvlnnDd911l64lLnI2inrJ43tDYKipUf7OMAzP0PWbNMGbiJzGm2++yZtvvsmOHTsAaNu2LU8//TRXXOEeAWQYBs888wxTp04lIyODbt268frrr9O2bVsTU4uI+IYDOQf4d8q/OZR3iJaRLXn9stcJtgabHUvKqFRF+bBhw2jUqBF+fqUbArF7926uuuoqFeUiZ2Pjd+7vXjh0feWuDLYezCE4wI+rOjYwO46IeLFGjRrx/PPP06JFCwCmT5/Otddeyx9//EHbtm2ZOHEikyZN4v3336dly5aMHTuWxMRENm7cqPcRIiKncST/CINTBrM3ey+NwxvzduLb1LLVKtPlLcU7lHpcw/Lly6lfv3SzK+ufqMhZyjoAe5e7b7fsa26Wk/hs2R4A+nWIJcym4VEicmpXX311sfvPPfccb775Jr/++itt2rRh8uTJjB49muuvvx5wF+3R0dHMmDGDwYMHmxFZRMTr5dhzGPLDELYe3Ur9kPq8k/QOdYPrmh1LyqlU76bHjBlDWFhYqTf6xBNPEBUVVe5QIjXe5u/d3xt0hohYc7P8TU6Bg9lr9gFw83kaui5S3eXn5xMUFFQh23I6nXz++efk5ORw4YUXsn37dlJTU0lKSvKsY7PZ6NWrF0uXLj1lUV5QUEBBQYHnfmZmJgB2u71UPURF66g3qWzUbuWntisftdvJ5TvyeXDBg/x1+C9q22rzxiVvUM9Wr0R7qd3KriLbrizbKHVRXhajRo0q0/oi8jeeoetXmpvjJL79cz85hU6a1Q2la5NIs+OISCVwuVw899xzvPXWWxw4cIBNmzYRHx/PU089RdOmTbnnnnvKtL0///yTCy+8kPz8fMLCwvj6669p06YNS5cuBSA6OrrY+tHR0ezcufOU2xs/fjzPPPNMieXz5s0jJCSk1LlSUlJKva4cp3YrP7Vd+ajdjnMaTj7J+YQNjg3YsHFrwK1sWLKBDWwosa7arfwqou1yc3NLva7GnYp4m8Jc2DrffdsLzyf//NgEb/27NsJisZicRkQqw9ixY5k+fToTJ05k0KBBnuXt27fn5ZdfLnNR3qpVK1atWsWRI0f48ssvufPOO1m4cKHn8b//LTEM47R/X0aNGsXw4cevv5uZmUlcXBxJSUmluna63W4nJSWFxMREAgICyvSz1GRqt/JT25WP2q04l+Hi6V+eZsPRDdj8bEzpPYVzo88tsZ7arfwqsu2KRnGVRpmL8gMHDjBixAh+/PFH0tLSMAyj2ONOp7OsmxSRE21fCI48qBUH0e3MTlPM1oPZLNuRgZ/Vwo1ddG1ykerqgw8+YOrUqVx22WXce++9nuUdOnRgw4aSvTFnEhgY6JnorWvXrixbtoxXXnmFxx57DIDU1FRiY4+fqpOWllai9/xENpsNm81WYnlAQECZ3kSVdX1xU7uVn9qufNRu7g8rx/02jjk75uBv8eelXi9xQaMLTvsctVv5VUTbleX5ZS7KBw4cyK5du3jqqaeIjY1VT5lIRSu6FFqrK8DLjq/Pl7sneOvdsh71IyrmHFMR8T579+71FNEncrlcFXKenWEYFBQU0KxZM2JiYkhJSaFz584AFBYWsnDhQiZMmHDW+xERqS6mrJrCzI0zsWBh7EVj6RXXy+xIUoHKXJQvXryYn3/+mU6dOlVCHJEazuWCjXPdt71s1nWH08WXK91F+U2a4E2kWmvbti0///wzTZo0Kbb8888/9xTPpfXEE09wxRVXEBcXR1ZWFjNnzmTBggXMnTsXi8XCsGHDGDduHAkJCSQkJDBu3DhCQkIYMGBARf5IIiI+a/ra6UxdMxWA0d1G0y++n8mJpKKVuSiPi4srMWRdRCrIvj8gJw0Cw6HpRWanKWbBxoMczCqgblggl7Yu3eURRcQ3jRkzhttvv529e/ficrn46quv2LhxIx988AGzZ88u07YOHDjA7bffzv79+6lVqxYdOnRg7ty5JCYmAjBy5Ejy8vIYOnQoGRkZdOvWjXnz5unyqiIiwNebv+bF5S8C8GDnB7m59c0mJ5LKUOaifPLkyTz++OO8/fbbNG3atBIiidRgRUPXW1wG/iXPlzTTp8cmeLu+SyMC/KwmpxGRynT11Vfz6aefMm7cOCwWC08//TRdunThm2++8RTTpfXuu++e9nGLxUJycjLJyclnkVhEpPqZt2Meyb8kAzCw7UD+1f5f5gaSSlPmovzmm28mNzeX5s2bExISUuIE9vT09AoLJ1LjeOml0NKy8vlpQxoAN3XVBG8iNcHll1/O5ZdfbnYMEZEaaenepTz282O4DBc3JNzA8HOHay6vaqxcPeUiUgkydkDaWrD4QULZeqIq29cr9+J0GXRpXJsW9TWkVERERKSyrEpbxbAFw3C4HCQ1SeKpC55SQV7Nlbkov/POOysjh4gUTfDW+AIIiTI3ywkMw+CzY0PXb+qqCd5EaoLIyMiTvgG0WCwEBQXRokULBg4cyF133WVCOhGR6mtj+kaG/jiUPEcePRr24PmLn8fP6md2LKlkpSrKMzMziYiI8Nw+naL1RKSMTrwUmhdZuesIWw/mEBzgR78OsWd+goj4vKeffprnnnuOK664gvPPPx/DMFi2bBlz587lvvvuY/v27QwZMgSHw8GgQYPMjisiUi3szNzJv1P+TVZhFp3rd+bl3i8T4KfrjNcEpSrKIyMj2b9/P/Xr16d27don/fTcMAwsFgtOp7PCQ4pUe/mZsHOJ+7aXnU/+2TJ3L3m/DrGEB+kfg0hNsHjxYsaOHcu9995bbPnbb7/NvHnz+PLLL+nQoQOvvvqqinIRkQqQmpPKoHmDSM9Pp3VUa6ZcNoVg/2CzY0kVKVVR/tNPPxEV5R5OO3/+/EoNJFITWbb9CC4H1G0JdZqbHccjp8DB7DX7AA1dF6lJvv/+eyZMmFBi+WWXXcYjjzwCwJVXXsnjjz9e1dFERKqd9Px0/p3yb/bn7KdJRBPe7PMmEYEafVyTlKoo79Wr10lvi0jFsG46dj65lw1d//bP/eQUOmlWN5TzmkaaHUdEqkhUVBTffPMNDz/8cLHl33zzjedD+pycHF1LXETkLGUXZjPkhyFsP7qd6JBo3kl8h7rBdc2OJVWszBO9AeTn57NmzRrS0tJwuVzFHrvmmmsqJJhITWExHFi2/uC+42VD1z8/NsFb/66NNOunSA3y1FNPMWTIEObPn8/555+PxWLh999/Z86cObz11lsApKSk6IN6EZGzkO/I5/6f7mfd4XVE2iKZmjSV2DDN31MTlbkonzt3LnfccQeHDh0q8ZjOKRcpuzrZm7DkH4WQOtDoPLPjeGw9mM2yHRn4WS3c2EXXJhepSQYNGkSbNm2YMmUKX331FYZh0Lp1axYuXEj37t0BPMPYRUSk7OwuO48sfIQVB1YQFhDGW4lvEV8r3uxYYpIyF+X3338//fv35+mnnyY6OroyMonUKDFH/3DfSLgcvOiSFx//uguA3i3rUT8iyOQ0IlLVevToQY8ePcyOISJS7bgMF08ufpJFexZh87Px2qWv0aZOG7NjiYnKXJSnpaUxfPhwFeQiFcEwiC4qyr3ofPIDmfl8/NtOAO7o3tTcMCJiqry8POx2e7FluvypiEj5GIbBuN/GMWf7HPwt/kzqPYmuMV3NjiUms5b1CTfeeCMLFiyohCgiNdChTYQVpmH4BULzS81O4/HG/C0UOFx0bRJJzwRNNiJS0+Tm5nL//fdTv359wsLCiIyMLPYlIiLl89ofr/Hpxk+xYGHcxePo2ain2ZHEC5S5p3zKlCn079+fn3/+mfbt2xMQUPy6xQ8++GCFhROp7qyb3bOuG017YrGFmZzGbU9GLjN+dw9dfySplSZ4E6mBHn30UebPn88bb7zBHXfcweuvv87evXt5++23ef75582OJyLik97/633e+fMdAJ684EmuaOY9oyTFXGUuymfMmMH3339PcHAwCxYsKPaG3WKxqCgXKQPLhm8AMBIuNznJcVN+2oLdadC9eR0ubF7H7DgiYoJvvvmGDz74gN69e3P33Xdz8cUX06JFC5o0acLHH3/MbbfdZnZEERGf8sWmL3hpxUsADOsyjJta3WRyIvEmZS7Kn3zySZ599lkef/xxrNYyj34XkSIH1mLdvwoXfrha9cMbpnjbcSiHz1fsAeCRpJYmpxERs6Snp9OsWTPAff54eno6ABdddBFDhgwxM5qIiM+Zu2Muz/7yLAB3t7ube9rfY3Ii8TZlrqoLCwu5+eabVZCLnK2VHwKQWqszhNU3OYzbqz9uxukyuKRVPc5tEmV2HBExSXx8PDt27ACgTZs2fPbZZ4C7B7127drmBRMR8TGL9y5m1M+jMDDo37I/w7oMMzuSeKEyV9Z33nknn376aWVkEak57PmwZiYAO+v0MjmM25a0LL5etReA4YmtTE4jIma66667WL16NQCjRo3ijTfewGaz8fDDD/Poo4+anE5ExDesPLCSh+c/jMPloG/TvozuNlpz9chJlXn4utPpZOLEiXz//fd06NChxERvkyZNqrBwItXWhtmQl4ER3oC0iPZmpwHg5R82Yxhwedto2jeqZXYcETHRww8/7Ll9ySWXsGHDBpYvX07z5s3p2LGjiclERHzDhvQN3P/j/eQ787mo4UWMu2gcflZvOFlRvFGZi/I///yTzp07A/DXX38Ve0yf/IiU0h/uoeuujrdCjvmngqzbl8m3a/ZjscDDiTqXXESKa9y4MRERERq6LiJSCjuO7mBwymCy7Fl0qd+FSb0nEeAXcOYnSo1V5qJ8/vz5lZFDpObI2AHbFgAWXB1vg6V/neEJle/lHzYBcFWHBrSOiTA5jYiYbcKECTRt2pSbb74ZgJtuuokvv/ySmJgY5syZo95yEZFTSM1JZVDKINLz0zkn6hymXDaFYP9gs2OJlzO/i06kpvnjI/f3+F5Qu7G5WYDVu4+Qsu4AVgsM65NgdhwR8QJvv/02cXFxAKSkpJCSksJ3333HFVdcoXPKRURO4XDeYQbNG0RqTipNI5ryZp83CQ8MNzuW+IBSFeXXX389mZmZpd7obbfdRlpaWrlDiVRbLif88bH7dpc7zM1yzEsp7l7yf3RuRPN6YSanERFvsH//fk9RPnv2bG666SaSkpIYOXIky5YtMzmdiIj3ySrMYsgPQ9iRuYOY0BimJk6lTnAds2OJjyhVUf6///2PgwcPkpmZecavo0eP8s0335CdnV3Z2UV8z5YfIWsfBEdC66vMTsOyHeks2nQQf6uFhy5TL7mIuEVGRrJ7924A5s6dS58+fQAwDAOn02lmNBERr5PnyOP+H+9nffp6ooKieCfxHWLDYs2OJT6kVOeUG4ZBy5aa/EnkrK2c7v7e4Rbwt4HdbloUwzB48fuNAPTvGkfjOiGmZRER73L99dczYMAAEhISOHz4MFdccQUAq1atokWLFianExHxHnannUcWPMLKtJWEBYTxVp+3aFqrqdmxxMeUqigvz+RuDRs2LPNzRKq17DTYNNd9u8vt5mYBlm49zG/b0wn0s/LApXqTLSLHvfzyyzRt2pTdu3czceJEwsLcp7bs37+foUOHmpxORMQ7OF1Onlj8BD/v/ZkgvyBev+x1zqlzjtmxxAeVqijv1atXZecQqf5WfwIuBzTsCtFtTY1iGAYvzXP3kg/o1pgGtTUrqIgcFxAQwIgRI0osHzZsWNWHERHxQoZhMPa3sczdMRd/qz8vX/IyXaK7mB1LfFSZL4kmIuVgGLDyA/dtL+glX7DxICt3HSEowMrQS5qbHUdEvMwHH3xw2sfvuMM7JqoUETGDYRhMWjGJLzZ9gQUL4y8ez0UNLzI7lvgwFeUiVWHXr3B4CwSEQrsbTI1iGAYvpbh7ye+8sCn1w4NMzSMi3uehhx4qdt9ut5Obm0tgYCAhISEqykWkxnK6nDz323N8vulzAJ6+8Gn6Nu1rcirxdSrKRapCUS95u3+AzdzrVX6/9gB/7c0kNNCPwb3USy4iJWVkZJRYtnnzZoYMGaLrlItIjWV32hm1eBTf7/geCxaeuvApbmx5o9mxpBoo1SXRROQs5B+FtV+7b3c2t3fJ5TJ4+dh1ye++qBlRoYGm5hER35GQkMDzzz9fohddRKQmyLXn8sBPD/D9ju/xt/ozsddE+rfsb3YsqSbKVZQ7HA5++OEH3n77bbKysgDYt2+frk0ucjJ/fQmOPKjbCuLONzXK7D/3s/FAFhFB/vzr4nhTs4iI7/Hz82Pfvn1mxxARqVJHC47y75R/s2TfEoL9g5ly6RQNWZcKVebh6zt37qRv377s2rWLgoICEhMTCQ8PZ+LEieTn5/PWW29VRk4R3+WZ4O0OsFhMi+Fwuph8rJd80MXx1AoOMC2LiHi3WbNmFbtvGAb79+9nypQp9OjRw6RUIiJV72DuQQb/MJjNGZuJCIzg9ctep1P9TmbHkmqmzEX5Qw89RNeuXVm9ejV16tTxLP/HP/7Bv/71rwoNJ+Lz9q+BfX+ANQA63mJqlK//2Mu2QzlEhgRw10XNTM0iIt7tuuuuK3bfYrFQr149Lr30Ul566SVzQomIVLHdWbv597x/syd7D/WC6/F24tskRCaYHUuqoTIX5YsXL2bJkiUEBhY/F7VJkybs3bu3woKJVAt/fOj+3vpKCK1rWoxCh4tXf9oMwJDezQmzaY5HETk1l8tldgQREVNtytjEvSn3cjDvII3CGjE1aSpx4XFmx5JqqszvzF0uF06ns8TyPXv2EB5u7qzSIl7FngdrPnXf7mLuBG+fr9jN7vQ86oXbuP2CpqZmEREREfFmq9JWMfTHoWQVZpEQmcDbfd6mXkg9s2NJNVbmid4SExOZPHmy577FYiE7O5sxY8Zw5ZVXljvI+PHjsVgsDBs2zLPMMAySk5Np0KABwcHB9O7dm7Vr15Z7HyJVav1s98zrteIg/hLTYuTbnUz5aQsA9/VuTnCgn2lZRERERLzZ0r1L+XfKv8kqzKJjvY5Mu3yaCnKpdGUuyl9++WUWLlxImzZtyM/PZ8CAATRt2pS9e/cyYcKEcoVYtmwZU6dOpUOHDsWWT5w4kUmTJjFlyhSWLVtGTEwMiYmJnhnfRbzayunu751uA6t5hfAnv+9i/9F8YmsFccv5jU3LISIiIuLNvt/xPff9dB95jjx6NOjB1MSp1LLVMjuW1ABlLsobNGjAqlWrGDFiBIMHD6Zz5848//zz/PHHH9SvX7/MAbKzs7ntttt45513iIyM9Cw3DIPJkyczevRorr/+etq1a8f06dPJzc1lxowZZd6PSJVK3wY7fgYs0Pk202LkFTp5ff5WAB64NIGgAPWSi4iIiPzd55s+59GFj+JwOejbtC+vXfoaIQEhZseSGqJcsz0FBwdz9913c/fdd591gPvuu49+/frRp08fxo4d61m+fft2UlNTSUpK8iyz2Wz06tWLpUuXMnjw4JNur6CggIKCAs/9zMxMAOx2O3a7/bRZih4/03pSktquOOvyD/ADXPGX4AyNhVO0S2W327Ql2zmUXUBcZDDXdYyuVr8fvebKR+1WfhXZdmp/ERHvYBgG7/71Lq+sfAWA/i37M7rbaPxMHOUoNU+5ivK9e/eyZMkS0tLSSszQ+uCDD5Z6OzNnzmTlypUsW7asxGOpqakAREdHF1seHR3Nzp07T7nN8ePH88wzz5RYPm/ePEJCSvdpV0pKSqnWk5LUdmAxnCT9NQ0/YIWrDfvmzDnjcyqj3fId8PoffoCFnlHZpHw/t8L34Q30misftVv5VUTb5ebmVkCSytO0aVPuvvtuBg4cSOPGOu1FRKonwzCYtGIS7699H4BB7QfxQOcHsFgs5gaTGqfMRfm0adO49957CQwMpE6dOsVetBaLpdRF+e7du3nooYeYN28eQUFBp1zv7weFYRinPVBGjRrF8OHDPfczMzOJi4sjKSmJiIiI02ay2+2kpKSQmJhIQEBAqX4OcVPbHWfZ/D3+q45ghNSh082j6ORvO+W6ldluU+ZvJcexlfi6ITx5e3f8/cp8topX02uufNRu5VeRbVc0istbPfLII7z//vs8++yzXHLJJdxzzz384x//wGY79d8zERFf4nA5ePaXZ/l6y9cAjOg6gjvb3mlyKqmpylyUP/300zz99NOMGjUKq7X8b/JXrFhBWloa5557rmeZ0+lk0aJFTJkyhY0bNwLuHvPY2FjPOmlpaSV6z09ks9lO+qYhICCg1G+iyrKuFKe2A1a75zywdLyVgOCwUj2lotvtaK6d95a6R5QMS2xFcFD1fSOt11z5qN3KryLaztvb/oEHHuCBBx5g9erVvPfeezz44IMMHTqUAQMGcPfdd9OlSxezI4qIlFuhs5DHFj3GD7t+wGqxknxhMv9I+IfZsaQGK3NVnZubyy233HJWBTnAZZddxp9//smqVas8X127duW2225j1apVxMfHExMTU2yYYGFhIQsXLqR79+5ntW+RSpOVCpuODRPvfLtpMd75eRtZ+Q5aRYdzVfvYMz9BROQkOnbsyCuvvMLevXsZM2YM//3vfznvvPPo2LEj7733HoZhmB1RRKRMcuw5DP1xKD/s+oEAawCTek1SQS6mK3NP+T333MPnn3/O448/flY7Dg8Pp127dsWWhYaGUqdOHc/yYcOGMW7cOBISEkhISGDcuHGEhIQwYMCAs9q3SKVZ/QkYTmh0PtRvbUqEw9kFTFuyHYDhSS2xWnVelIiUj91u5+uvv2batGmkpKRwwQUXcM8997Bv3z5Gjx7NDz/8oCuiiIjPOJJ/hKE/DuXPQ38S4h/CK5e+wgWxF5gdS6TsRfn48eO56qqrmDt3Lu3bty8xBG/SpEkVFm7kyJHk5eUxdOhQMjIy6NatG/PmzSM8PLzC9iFSYQwDVn7gvt3lDtNivL1oGzmFTto3rEVSm1Of6iEiciorV65k2rRpfPLJJ/j5+XH77bfz8ssv07r18Q8bk5KS6Nmzp4kpRURK70DOAQanDGbr0a3UttXmzT5v0q5uuzM/UaQKlLkoHzduHN9//z2tWrUCKDHR29lYsGBBsfsWi4Xk5GSSk5PParsiVWLnEvf1yQPDoK05w6DSMvOZvnQH4O4l1+yhIlIe5513HomJibz55ptcd911Jz0Hvk2bNtxyyy0mpBMRKZudmTv597x/sy9nH/VD6jM1cSrNazc3O5aIR5mL8kmTJvHee+8xcODASogj4sNWfuj+3u56sJVugreK9saCrRQ4XHRpXJveLeuZkkFEfJvT6eTdd9/lmmuuISoq6pTrhYaGMm3atDNub/z48Xz11Vds2LCB4OBgunfvzoQJEzwf7oP7yirPPPMMU6dO9YyMe/3112nbtm2F/EwiUnNtSN/A4JTBpOen0ySiCVMTp9IgrIHZsUSKKfNsbTabjR49elRGFhHflXcE1v2f+3YXcy6nsfdIHjN+2wXAiKRW6iUXkXLx8/Pj3nvv5ejRoxWyvYULF3Lffffx66+/kpKSgsPhICkpiZycHM86EydOZNKkSUyZMoVly5YRExNDYmIiWVlZFZJBRGqmlQdWcvfcu0nPT6d1VGve7/u+CnLxSmUuyh966CFee+21ysgi4rv+/Bwc+VC/DTQ898zrV4IpP22m0Oniwvg6dG9R15QMIlI9tG/fnm3btlXItubOncvAgQNp27YtHTt2ZNq0aezatYsVK1YA7l7yyZMnM3r0aK6//nratWvH9OnTyc3N1SRyIlJui/YsYnDKYLLsWXSp34X3Ln+PusF6fyTeqczD13///Xd++uknZs+eTdu2bUucZ/bVV19VWDgRn/HHsaHrnW8HE3qodx7O4fPlewB4JKllle9fRKqX5557jhEjRvCf//yHc889l9DQ0GKPR0RElHvbRT3wRUPjt2/fTmpqKklJSZ51bDYbvXr1YunSpQwePLjENgoKCigoKPDcz8zMBNyzxdvt9jNmKFqnNOvKcWq38lPblU952+27Hd8x5pcxOAwHFzW4iAkXTSDIElRj2l+vt/KryLYryzbKXJTXrl2b66+/vqxPE6m+9q2C/avBLxA63GxKhFd+3IzDZdCrZT26Nj31OaAiIqXRt29fAK655ppip8IYhoHFYsHpdJZru4ZhMHz4cC666CLP5U9TU1MBiI4ufrWI6Ohodu7cedLtjB8/nmeeeabE8nnz5hESElLqPCkpKaVeV45Tu5Wf2q58ytJuvxb8yrd532Jg0CGgA4k5icyfN78S03kvvd7KryLaLjc3t9TrlrkoL82kLiI1SlEveeurILROle9+S1o2//fHXgCGJ6qXXETO3vz5lfMG9v7772fNmjUsXry4xGN/nwej6AOAkxk1ahTDhw/33M/MzCQuLo6kpKRS9eLb7XZSUlJITEw86czycnJqt/JT25VPWdrNMAz++9d/mf3nbABubnkzj577KFZLmc/W9Xl6vZVfRbZd0Siu0ihzUS4iJ7DnwZrP3be73G5KhMk/bMJlQGKbaDrG1TYlg4hUL7169arwbT7wwAPMmjWLRYsW0ahRI8/ymJgYwN1jHhsb61melpZWove8iM1mw2azlVgeEBBQpjdRZV1f3NRu5ae2K58ztZvLcPHCshf4aP1HAAzpOIQhHYfU+Elv9Xorv4pou7I8v1RFeZcuXfjxxx+JjIykc+fOp32Br1y5stQ7F/F562ZBwVGo1Ria9a7y3a/fn8nsNfsB9ZKLSMU6cuQI7777LuvXr8disdCmTRvuvvtuatWqVabtGIbBAw88wNdff82CBQto1qxZscebNWtGTEwMKSkpdO7cGYDCwkIWLlzIhAkTKuznEZHqyeFyMGbpGGZtnQXA4+c/zm3n3GZyKpGyKVVRfu2113o+kb7uuusqM4+Ib1n5gft7l9vBWvXDo15O2QRAvw6xnBNb/omXREROtHz5ci6//HKCg4M5//zzMQyDSZMm8dxzzzFv3jy6dOlS6m3dd999zJgxg//973+Eh4d7ziGvVasWwcHBWCwWhg0bxrhx40hISCAhIYFx48YREhLCgAEDKutHFJFqoMBZwIiFI1iwewF+Fj/+0+M/XN38arNjiZRZqYryMWPGcPfdd/PKK68wZsyYys4k4hsOb4WdiwELdKr6N45r9hxh3roDWC3wcJ+EKt+/iFRfDz/8MNdccw3vvPMO/v7utwoOh4N//etfDBs2jEWLFpV6W2+++SYAvXv3LrZ82rRpDBw4EICRI0eSl5fH0KFDycjIoFu3bsybN4/w8PAK+XlEpPrJLszmwfkPsix1GYHWQF7q/RK943qbHUukXEp9Tvn06dN5/vnn9Q9SpEjRBG8t+kCtRqdftxK8NM/dS35dp4a0qK/jUkQqzvLly4sV5AD+/v6MHDmSrl27lmlbhmGccR2LxUJycjLJyclljSoiNVB6fjpDfhjCusPrCA0I5bVLX+O8mPPMjiVSbqUeb1uaf6oiNYbTDqtmuG93uaPKd798RzoLNx3Ez2rhIfWSi0gFi4iIYNeuXSWW7969Wx/Oi4ipUnNSufO7O1l3eB1RQVG8d/l7KsjF55XpJNiaPoOhiMfmeZB9AELqQsu+Vb77ol7ym7o2okmd0Crfv4hUbzfffDP33HMPn376Kbt372bPnj3MnDmTf/3rX9x6661mxxORGmr70e3c/t3t7MjcQUxoDO/3fZ82ddqYHUvkrJXpkmgtW7Y8Y2Genp5+VoFEfMLKY0PXO90K/oFVuuulWw7xy7bDBPpZuf9S9ZKLSMV78cUXsVgs3HHHHTgcDsB9aZchQ4bw/PPPm5xORGqidYfXcW/KvWQUZNCsVjOmJk4lJjTG7FgiFaJMRfkzzzxT5kuhiFQ7mftg8/fu252rdui6YRi8dGzG9VvPj6Nh7eAq3b+I1AyBgYG88sorjB8/nq1bt2IYBi1atCAkJMTsaCJSA604sIJhi4aRY8+hTZ02vNnnTaKCosyOJVJhylSU33LLLdSvX7+ysoj4hlUzwHBB4wuhXtVeG3zBpoOs2JmBzd/KfZe0qNJ9i0jNExISQvv27c2OISI12Hr7ep6d/yyFrkLOjzmfVy55hbDAMLNjiVSoUhflOp9cBHC54I+P3Lc7316luzYMg0nHziW/48Im1I8IqtL9i0jNkZ+fz2uvvcb8+fNJS0vD5XIVe3zlypUmJRORmmT2ttl8kvMJLlxcEncJL/R6AZufzexYIhWu1EW5Zl8XwX1d8oztEBgOba+r0l3PW3eAP/ceJSTQj3t7Na/SfYtIzXL33XeTkpLCjTfeyPnnn68P5kWkSjlcDl5Z+Qrvr30fgKvjr+bZHs/iby3TIF8Rn1HqV/bfPyUXqZFWfuD+3v5GCKy6Wc9druO95Hf1aEqdMH1KLCKV59tvv2XOnDn06NHD7CgiUsMczjvMyEUj+T31dwB62noyptsYFeRSrenVLVJaeRmwbpb7dpeqHbr+7Z/72Xggi/Agf/59sXrJRaRyNWzYUNcjF5Eqt+bgGoYvGM6B3AOE+IfwzAXPUPBXAVZLma7iLOJz9AoXKa01n4OzAKLbQYMuVbZbh9PFyz+4e8kHXRxPrZCAKtu3iNRML730Eo899hg7d+40O4qI1ACGYfDZxs8YOHcgB3IP0DSiKZ/0+4TLGl9mdjSRKqGecpHSMIzjQ9e73AFVeH7l/1btY9vBHGqHBHBXj6ZVtl8Rqbm6du1Kfn4+8fHxhISEEBBQ/MPA9PR0k5KJSHWT78jnud+e4/+2/B8AfRr34T89/kNYYBh2u93ccCJVREW5SGnsXwUH/gQ/G7TvX2W7tTtdTP7R3Ut+b6/mhAepl1xEKt+tt97K3r17GTduHNHR0ZroTUQqxd7svTw8/2HWp6/HarHyYOcHubvd3fqbIzWOinKR0ijqJT/nagiJqrLdfr58D7vT86gbFsgdFzapsv2KSM22dOlSfvnlFzp27Gh2FBGpppbuXcrIn0dytOAokbZIJvaayAWxF5gdS8QUKspFzqQwF/78wn27yx1Vttt8u5PXftoMwNDeLQgJ1OEqIlWjdevW5OXlmR1DRKohl+Hi3T/f5bU/XsPAoG2dtrzc+2Viw2LNjiZiGk30JnIm6/4HBZlQuwk0vbjKdjvz913sP5pPTEQQA7o1rrL9iog8//zzPPLIIyxYsIDDhw+TmZlZ7EtEpDyyCrMYNn8Yr/7xKgYGNyTcwPQrpqsglxpPXW8iZ+KZ4O12sFbN51h5hU6mzN8KwP2XtiAowK9K9isiAtC3b18ALrus+MzHhmFgsVhwOp1mxBIRH7YlYwsPL3iYHZk7CLAG8ES3J7ix5Y1mxxLxCirKRU7n0GbYtRQsVuh0W5Xt9sNfd3Aou4BGkcHc1DWuyvYrIgIwf/58syOISDUyd8dcnl7yNHmOPGJCY5jUaxLt67U3O5aI11BRLnI6f3zo/p6QBBENqmSX2QUO3lzg7iV/8LIEAv11lomIVK1evXqZHUFEqgGHy8HLK17mg3XuUYfdYroxsddEooKqbtJcEV+gd/sip+K0w6oZ7tudb6+y3b6/ZDsZuXaa1Q3l+s4Nq2y/IiIn+vnnn/nnP/9J9+7d2bt3LwAffvghixcvNjmZiPiCQ3mHGDRvkKcgv6vdXbyV+JYKcpGTUFEuciqb5kLOQQitDy0vr5JdHs218/aibQAM65OAv58OURGpel9++SWXX345wcHBrFy5koKCAgCysrIYN26cyelExNutPriam2ffzPIDywnxD2FS70kMP3c4/lYN0hU5Gb3jFzmVogneOg0Av4Aq2eV/F28jK99By+gwru5QNcPlRUT+buzYsbz11lu88847BAQc//vXvXt3Vq5caWIyEfFmhmHw6YZPGTh3IGm5aTSr1YxP+n1CYpNEs6OJeDV9XCVyMkf3wpYf3LeraOh6ek4h7y3eDsDwxJZYrZYq2a+IyN9t3LiRnj17llgeERHBkSNHqj6QiHi9fEc+//n1P8zaOguAxCaJ/KfHfwgNCDU5mYj3U1EucjKrZoDhgiY9oG6LKtnl2wu3klPopG2DCC5vG1Ml+xQROZnY2Fi2bNlC06ZNiy1fvHgx8fHx5oQSEa+1J2sPwxcMZ336eqwWKw91eYi72t6FxaIOBpHSUFEu8ncuF/xRdG3yO6pklwezCpj+yw4AHklqqX9iImKqwYMH89BDD/Hee+9hsVjYt28fv/zyCyNGjODpp582O56IeJEle5fw2M+PcbTgKJG2SCb2msgFsReYHUvEp6goF/m7HYvgyC6wRcA511TJLt9atJ18u4vOjWtzSav6VbJPEZFTGTlyJEePHuWSSy4hPz+fnj17YrPZGDFiBPfff7/Z8UTEC7gMF//9879M+WMKBgbt6rRjUu9JxIbFmh1NxOeoKBf5u6IJ3tr3h8CQSt9dRgF8sno3AI8ktlIvuYh4heeee47Ro0ezbt06XC4Xbdq0ISwszOxYIuIFsgqzeGLxEyzYvQCAGxJuYFS3Udj8bKbmEvFVKspFTpSbDuu/cd+uoqHr8/ZasTsNujWLokeLOlWyTxGR0ggJCaFr165mxxARL7I5YzMPL3iYnZk7CbAGMLrbaG5oeYPZsUR8mopykROt+QychRDTHhp0qvTd7UrP5dc0d8/4I0nqJRcRc919992lWu+9996r5CQi4o3mbp/L00ufJs+RR0xoDC/3fpl2dduZHUvE56koFyliGLByuvt2lzurYHcGL87bjMuwcFGLOpzfLKrS9ykicjrvv/8+TZo0oXPnzhiGYXYcEfESdpedl1e8zIfrPgSgW2w3JvacSFSQ3ruIVAQV5SJF9q6EtHXgHwTtb6z03b27eDvfrT2ABYOHL6uay66JiJzOvffey8yZM9m2bRt33303//znP4mK0ptukZrsUN4hHl34KMsPLAfg7nZ380DnB/C3qowQqShWswOIeI2iy6C1uRaCIyt1Vws2pjFuznoArmvqokOjWpW6PxGR0njjjTfYv38/jz32GN988w1xcXHcdNNNfP/99+o5F6mBVh9czc3f3MzyA8sJ8Q/h5d4v8/C5D6sgF6lgKspFAAqy4c8v3Lc7316pu9p6MJsHPvkDlwE3dmlIrxi90RUR72Gz2bj11ltJSUlh3bp1tG3blqFDh9KkSROys7PNjiciVcAwDD7d8CkD5w4kLS+NZrWa8clVn9CnSR+zo4lUSyrKRQDW/R8UZkNUPDS9qNJ2czTXzqDpy8nKd3Buk0iSrz4Hze0mIt7KYrFgsVgwDAOXy2V2HBGpAvmOfJ5c8iRjfxuLw+UgsUkin/T7hPha8WZHE6m2VJSLAKx0T1xC59uprCrZ4XTxwMw/2HYohwa1gnjrn+di89chKCLepaCggE8++YTExERatWrFn3/+yZQpU9i1a5euUy5Sze3J2sMd393BrK2zsFqsDD93OC/1eonQgFCzo4lUazohROTgRtj9K1j8oNOAStvN899tYNGmgwQFWJl6R1fqhduw2+2Vtj8RkbIaOnQoM2fOpHHjxtx1113MnDmTOnXqmB1LRKrAkr1LGLloJJmFmUTaInmh1wt0i+1mdiyRGkFFucjKYxO8tbwcwmMqZRefL9/NfxdvB+Cl/p1o11ATu4mI93nrrbdo3LgxzZo1Y+HChSxcuPCk63311VdVnExEKovLcPHOmnd4fdXrGBi0q9OOSb0nERsWa3Y0kRpDRbnUbI5CWD3TfbvLHZWyixU70xn99V8APHhZAv066J+ciHinO+64A4smuhCpMdLz0xmzZAwL9iwA4IaEGxjVbRQ2P5u5wURqGBXlUrNt+g5yD0FYDLRIrPDN7zuSx+APV1LodHF522iGXZZQ4fsQEako77//vtkRRKQKGIbB7G2zmbhsIkcKjhBoDWT0BaO5PuF6s6OJ1EgqyqVmKxq63mkA+FXs4ZBX6OTfHy7nUHYBrWPCmXRTJ6xW9UCJiIiIefZl7+PZX55lyb4lALSMbMl/evyHNnXamJxMpOZSUS4119E9sOVH9+3O/6zQTRuGwYgvVvPX3kyiQgN5546uhNp0uImIiIg5nC4nn2z4hFf/eJU8Rx6B1kCGdBrCnW3vJMAaYHY8kRpNVYLUXH98DBjQ9GKo07xCN/36/C18u2Y//lYLb97WhbiokArdvoiIiEhpbc7YTPLSZNYcWgNAl/pdSO6eTLNazUxOJiJg8nXKx48fz3nnnUd4eDj169fnuuuuY+PGjcXWMQyD5ORkGjRoQHBwML1792bt2rUmJZZqw+WEP45dm7yCJ3ibtzaVF+dtAuDZa9vRLV6XExIREZGqV+gs5PVVr3PT7JtYc2gNYQFhPHXBU0zrO00FuYgXMbUoX7hwIffddx+//vorKSkpOBwOkpKSyMnJ8awzceJEJk2axJQpU1i2bBkxMTEkJiaSlZVlYnLxedsWwNHdEFQLzrm6wja7ITWTYZ+uAuCOC5swoFvjCtu2iIiISGmtSltF/2/689bqt3C4HPSO683/Xft/3NTqJqwWU0sAEfkbU4evz507t9j9adOmUb9+fVasWEHPnj0xDIPJkyczevRorr/ePRvk9OnTiY6OZsaMGQwePNiM2FIdFPWSt78JAoIrZJPpOYX8a/pycguddG9eh6eu0oQpIiIiUrVy7Dm8svIVZm6YiYFBVFAUT3R7gqQmSbrkoYiX8qpzyo8ePQpAVFQUANu3byc1NZWkpCTPOjabjV69erF06dKTFuUFBQUUFBR47mdmZgJgt9ux2+2n3X/R42daT0ryqbbLPYz/+tlYAHuHAVABme1OF/d+uII9GXnERQYz+ab24HJidzlP/zxfajcvo7YrH7Vb+VVk26n9RaQyLNqziP/8+h9Sc1IBuK7FdYzoOoJatlomJxOR0/GaotwwDIYPH85FF11Eu3btAEhNdf9BiY6OLrZudHQ0O3fuPOl2xo8fzzPPPFNi+bx58wgJKd1kWykpKWWJLifwhbaLT5tLe5edI8FNWbhyN7D7rLf52TYrvx+wYvMzuK1xFr8s+KFMz/eFdvNWarvyUbuVX0W0XW5ubgUkERFxS89P5/nfn+e77d8B0DCsIWMuHMOFDS40OZmIlIbXFOX3338/a9asYfHixSUe+/tQG8MwTjn8ZtSoUQwfPtxzPzMzk7i4OJKSkoiIiDhtBrvdTkpKComJiQQE6NIQZeEzbWcY+L8zDoDwXvdx5blXnvUmP/59N0t+WY/FAq/c0pnLWtcv9XN9pt28kNqufNRu5VeRbVc0iqsmWLRoES+88AIrVqxg//79fP3111x33XWexw3D4JlnnmHq1KlkZGTQrVs3Xn/9ddq2bWteaBEfYRgGs7fNZuKyiRwpOILVYuX2c25naKehhAToyi8ivsIrivIHHniAWbNmsWjRIho1auRZHhMTA7h7zGNjYz3L09LSSvSeF7HZbNhsthLLAwICSv0mqizrSnFe33a7l8HBDeAfjF+nm/E7y6xLtx5i7LcbAHj08lb0bd+wXNvx+nbzYmq78lG7lV9FtF1NavucnBw6duzIXXfdxQ033FDi8aIJXd9//31atmzJ2LFjSUxMZOPGjYSHh5uQWMQ37Mvex7O/PMuSfUsAaBnZkme7P0vbuvpAS8TXmFqUG4bBAw88wNdff82CBQto1qz4pRmaNWtGTEwMKSkpdO7cGYDCwkIWLlzIhAkTzIgsvm7ldPf3tte5Z14/C7sO53LfxytxuAyu7dSAIb0q9lrnIiLVwRVXXMEVV1xx0sc0oatI2TldTj7Z8Amv/vEqeY48Aq2BDOk0hDvb3kmAteZ84CdSnZhalN93333MmDGD//3vf4SHh3vOIa9VqxbBwcFYLBaGDRvGuHHjSEhIICEhgXHjxhESEsKAAQPMjC6+qCAL/vrKffssr02eXeBg0AfLyci106FRLSbc0EEzmoqIlFF5JnSFs5vUtWi9E79L6ajdyq+i2m7LkS08+9uz/HX4LwA61+vMU92eomlEU3CC3Vm9fjd6zZWP2q38zJrU1dSi/M033wSgd+/exZZPmzaNgQMHAjBy5Ejy8vIYOnSo51yzefPmaUiblN3ar8GeA3VaQOPyT3zichkMm7mKjQeyqBduY+rtXQkK8KvAoCIiNUN5JnSFipnUFTThYXmp3cqvvG3nMBwszF/IooJFOHFiw8blwZfTtbAr6xavYx3rKjipd9FrrnzUbuVX1ZO6mj58/UwsFgvJyckkJydXfiCp3lZ+4P7e+XY4i17tSSmb+GH9AQL9rUy9/VxiagVVUEARkZqpLBO6wtlN6gqa8LC81G7ldzZtt/rgap797Vm2F2wHoFfDXow6bxT1Q0o/sayv0muufNRu5WfWpK5eMdGbSKVLWw97loHVHzreWu7NzFq9jynztwDw/PXt6dw4sqISiojUOOWZ0BUqZlLX8qwvbmq38itL2+XYc3hl5SvM3DATA4OooCie6PYESU2Satwpc3rNlY/arfyqelJX61ntScRXrPzQ/b1lXwg/9Ru90/lzz1Ee/Xw1AIN7xnN9l0ZneIaIiJzOiRO6Fima0LV79+4mJhMx16I9i7juf9fxyYZPMDC4rsV1zLpuFpc3vbzGFeQiNYF6yqX6cxTA6k/ct8s5wVtaVj6DPlhOgcPFJa3qMbJv6woMKCJSfWVnZ7NlyxbP/e3bt7Nq1SqioqJo3LixJnQVOUF6fjrP//48323/DoCGYQ0Zc+EYLmxQ/rlwRMT7qSiX6m/jHMhLh/AG0PyyMj893+5k8IcrSM3Mp3m9UF65tTN+Vn1KLSJSGsuXL+eSSy7x3C86F/zOO+/k/fff14SuIrjnUZi9bTYTl03kSMERrBYrt59zO0M7DSUkoPSTF4qIb1JRLtWbYcDy99y3Ow0Av7K95A3DYPTXf/HHriNEBPnz3zvPIyJI5+aIiJRW7969TzuxqyZ0lZpuX/Y+nv3lWZbsWwJAy8iWPNv9WdrWbWtyMhGpKirKpfpyFMKsB2D7IrBYofM/y7yJdxdv58uVe/CzWnj9ti40qxtaCUFFRESkpnG6nHyy4RNe/eNV8hx5BFoDGdJpCHe2vZMAqzoARGoSFeVSPeVlwKe3w46fweIHV0+GqGZl2sSCjWmMm7MegCf7ncPFCfUqIaiIiIjUNJszNpO8NJk1h9YA0KV+F5K7J9OsVtneq4hI9aCiXKqfjB3wcX84tAkCw+Gm96FFnzJtYuvBbB745A9cBtzcNY6B3ZtWRlIRERGpQQqdhUxdO5X//vlfHC4HYQFhPHzuw9zY8kasFl0USaSmUlEu1cueFfDJzZBzECIawoDPIKZdmTZxNNfOoOnLycp30LVJJM9e11aXHxEREZGzssuxi1u/u5XtmdsB6B3Xmye7PUl0aPku1Soi1YeKcqk+1n8DXw4CRx7EtHcX5BENyrQJh9PFAzP/YNuhHBrUCuKt28/F5u9XSYFFRESkujtacJTXVr7GZ9mfYWAQFRTFE92eIKlJkj70FxFARblUB4YBv74B348GDEhIghvfA1vZL6cz/rsNLNp0kOAAP965syt1w2wVn1dERESqvaMFR/lo/Ud8tO4jsu3ZAFwTfw0jzx9JLVstk9OJiDdRUS6+zeWEuY/D71Pd97veDVe8UOZLnwF8tnw37y52Dyl76aaOtG2gf5giIiJSNpmFmXy0zl2MZ9mzAGhRqwUXOS7iwQseJCBAM6uLSHEqysV3FWTDl/fAprnu+4n/ge4PQDmGgq3Ymc6TX/8FwEOXJXBl+9iKTCoiIiLV3EmL8dotGNppKD1jezL3u7kmJxQRb6WiXHxTVirMuAn2rwb/IPjH29D2unJtat+RPAZ/uJJCp4u+bWN46LKEis0qIiIi1VZmYSYfr/uYD9d9WKwYH9JxCH2a9MFqsWK3201OKSLeTEW5+J4Da+HjmyBzD4TUhVtnQtx55dpUXqGTf3+4nEPZBbSOCeelmzpitWrSFRERETm9rMIsPlr/kbsYLzxejN/b8V4SmyTqEmciUmoqysW3bP0JPrsTCjKhTgLc9jlENSvXpgzDYMQXq/lrbyZ1QgP5751dCbXpkBAREZFTUzEuIhVNFYj4jpUfwOyHweWAJj3g5o8gJKrcm3t9/ha+XbMff6uFN/95Lo0iQyowrIiIiFQnWYVZfLz+Yz5Y94GnGG9eqzn3drqXpCZJKsZFpNxUlIv3Mwz4aSz8/KL7fvub4Nop4F/+y5V9vzaVF+dtAuA/17Xj/GblL+5FRESk+souzOaj9R8VK8bja8UzpOMQkpqqGBeRs6eiXLybowD+byj89YX7fs+RcMkT5ZphvciG1Ewe/nQVAAO7N+XW8xtXQFARERGpTrILsz0945mFmcDxYjyxSSJ+Vj+TE4pIdaGiXLxXbjrMvA12LQWrP1z9CnT+51ltMj2nkH9NX05uoZMeLerwZL9zKiisiIiIVAfZhdnM2DCD6WunFyvG7+3oHqauYlxEKpqKcvFOh7fCx/0hfSvYIuDmDyG+91lt0u50MeSjFezJyKNJnRBeH9AFfz8NORMREZGTF+PNajVzD1NXMS4ilUhFuXifXb/BzFsh9zDUinPPsF7/7Hu0k2et5bft6YTZ/PnvHV2pHRJYAWFFRETEl+XYc5ixfgbT103naMFRwF2M39vhXi5vermKcRGpdCrKxbus/Rq+GgzOAmjQGW79FMKjz3qzH/66k49/24XFAq/c0omE6PAKCCsiIiK+KseewycbPuH9te97ivGmEU25t+O99G3aV8W4iFQZFeXiHQwDlrwCP4xx3291JdzwXwgMPetN/7L1MM/MWgvAyMtbc9k5Z1/ki4iIiG9SMS4i3kZFuZjP6YA5I2DFNPf9bvfC5ePgLP8pZuXbeWPBVt5dvB2Hy+C6Tg24t1d8BQQWERERX1NUjE9fO50jBUcAdzE+uONgrmh6hYpxETGNinIxV0EWfD4QtvwAWKDveLhgyFlt0uF0MXPZbl5O2cThnEIAereqx/M3dMByFpdSExEREd9zsmK8SUQTBncYzBXNrsDfqrfDImIu/RUS8xzdCzNuhgN/gn8w3PgutO5X7s0ZhsGCjQcZN2c9m9OyAYivG8oTV57DZefUV0EuIiJSg+Tacz3D1FWMi4g3018jMcf+NTDjJsjaD6H1YcBMaHhuuTe3fn8m4+as5+fNhwCIDAlgWJ+WDOjWmABd9kxERKTGyLXnMnPjTN7/630yCjIAFeMi4t30V0mq3uYU95D1wmyo1xoGfAaRTcq1qbTMfF6at4nPV+zGZUCgn5W7ejRl6CUtqBUcULG5RURExGudrBhvHN6YwR0Hc2WzK1WMnyjvCOz+HXb9Art+hboJcM2rZqcSqbH010mq1vL34NsRYDihWU+46UMIrl3mzeQVOnnn5228tXAruYVOAPp1iOXxvq2Jiwqp4NAiIiLirbYd3cbsrbP5YtMXKsZP5eje4wX4rl/gwFrAOP545h7ToomIinKpKi4X/JjsvuwZQKfb4KrJ4B9Yxs0YfPXHXl78fiOpmfkAdG5cmyf7ncO5TaIqNrOIiIh4pUN5h/hu+3fM3jabdYfXeZbHhccxuMNg+sX3q7nFuGHAwY3HivBjX0d2lVwvKh4ad4fGF0DjC6s+p4h41NC/VlKl7Hnw9b2w7v/c9y8ZDT0fhTJOvLZ06yGe+3Y9a/dlAtAoMpjH+rbmqg6xmsRNRESkmsu15/Ljrh/5dtu3/LL/F1yGCwA/ix89Gvbg6vir6dOkT80rxh2FsH817Fp6rCf8V8hLL76OxQox7YsX4eHR5uQVkRJq2F8tqXI5h+CTW2HP72ANgGtfh443l2kTWw9mM37OBn5YfwCAcJs/91/agju7NyUoQNcUFRERqa4cLge/7v+V2dtm89Oun8hz5Hke61C3A/3i+9G3WV+igmrQaLn8TPf7qqICfM9yOKFdAPdVbRp1dRffTS6ERueBLdycvCJyRirKpfIc2gwf3wgZOyCoNtzyMTS9qNRPT88p5NUfN/PRrztxuAz8rBZu69aYhy5LoE6YrdJii4iIiHkMw2Dt4bXM3jab77Z/R3r+8V7fxuGNuSr+Kq6Mv5ImEeWbJNbnZKUePx9851I48BccGyXgERx1vABvfCHEdCjzKYIiYh4V5VI5diyBmQMg/wjUbgK3fQH1WpbqqQUOJ9OX7uC1n7aQle8AoM859Xn8inNoUT+sEkOLiIiIWXZn7ebbbd/y7bZv2ZG5w7M80hZJ32Z9uSr+KtrXbV+9T1kzDDi8xV2E7zx2PnjG9pLr1W5SvAiv27LMpwWKiPdQUS4Vb83n8L+h4CyEhl3h1pkQVu+MTzMMgzl/pvL83PXsTncPw2oTG8GT/c6he4u6lZ1aREREqtiR/CN8v+N7Zm+bzaqDqzzLbX42Lo27lKuaX8WFDS4kwFpNL3PqtEPqmuO94Lt+hdxDf1vJAtHtjhXgx84Hj2hgStzKlF3gYMehHLaf8LXtYDaph/248kqz04lULhXlUnEMA+viSbBwnPv+OdfA9VMhIPiMT125K4Pnvl3Pip3uS5nUD7fx6OWtuL5LI/ys+uRXRMxT4CzgUN4h9mfu55Dz72+WRaSs8h35LNyzkNnbZrN4z2IchntUnAUL3WK7cVX8VVzW+DLCAqvh6LjCbNi9+ngv+J7lYM8pvo6f7dj54Be4J2aLOw+CapmTt4IVOJzsOpzLtkM5ngK86HZaVsEpnmUhK99BVEA1/WBGBBXlUlGcdjrtehe/9EXu+90fgD7PgtV62qftTs9lwtwNzF6zH4DgAD8G94rn3z3jCQnUy1NEKodhGGQWZnIw9yCH8g9xMPcgh/MOczDvIIfyDnEo75DndlZhlud53W3duYM7TEwu4pucLifLDyzn223fkrIzhWx7tuexc6LOoV98P65odgX1Q+qbmLKCOe1waBOk/oV17wp6bpyH/6pdYDiLrxdU+1gBfqwIb9AJ/H137hyH08XeI3nFeryLvvYeycMwTv3cOqGBNKsbStO6oTSrG0rjyCB2r1tBcMDp30+K+DpVPXL29v2B3/dP0iR9MYbFiuWKiXD+oNM+JTPfzuvztzBtyQ4KHS4sFrixSyNGXN6K6IigKgouItWN3WnncP5hd1F9rOA+lHu8yD6x8La77KXebqA1kDrBdQh0aOIkkbLYlLGJ2Vtn8+32b0nLTfMsjw2NpV98P/o160eLyBYmJqwgeUfcE7Cl/gWpf7qHpB/c4D6VD/ADIovWrRV3fBh64wuhXuszdmJ4G8MwOJBZwLZD2ew4lMv2Q9mewntXei5256kr7zCbP82OFd1N64YSf8LtWsHFe8PtdjtzdoK/n2+1j0hZqSiX8nG5YEsKLH0NdvyMFXBYbXDjNPzb9Dvl0+xOF5/8vovJP2wmPcf9j6pHizo8ceU5tG1QPYZmiUjFMgyDHHtO8V7sUxTcGQUZZdp2RGAE9YLrUTe4LnVD6lI3qC71Qo7dD65LveB61AmuQ0RgBA6Hgzlz5lTSTylSfaTmpDJn+xxmb5vN5ozNnuXhAeEkNU3iqvir6BLdBavFBwstw3BfVeZAUfF97PvRXSdfPzAcYtrhrN+WPw760/Hqewmo26xKI5+NjJxCth0rtk8cbr7zcA65hc5TPi/Q30rTOiHHiu8wmtUNOfY9lLphgdV7sj6RclBRLmVjz4c1n8Ivr8Ohje5lVn9cbf7BQue59ExIOunTDMPgpw1pjJuznq0H3edONa8Xyuh+53BJq/r64yxSAxiGQYGzgGx7Njn2HPf3wpzjt+05ZBZmFi+8j93Od+aXej/+Fn/qBNcpVlTXC6lH3SB34e0pwoPrEuinnm+RipBVmMUPO39g9rbZLEtdhoG7pzTAGkDPRj25Kv4qLm50MTY/HxqWbc+DtPUnFOB/woG1UJB58vVrNYaY9hDTzv09up17lnSrFZfdzt45c+hYq1HV/gyl8PcJ1nYcK7y3H8rhaN6pRxT5WS3ERQZ7hprHnzDsvEGtYKyaE0ik1FSUS+nkpsOyd+H3tyHnoHtZYDh0HQjd7sUZEk32KXqQ1u47ynPfrmfp1sMARIUG8nCfBG45vzEBGo4k4vWcLie5jlx38VyYXbyotucUK7D//li2PZtce67n8aIJncojLCDMU0yf+PX3gruWrZZv9sCJ+Bi7087ivYuZvW02C3YvoNBV6Hns3Ohz6Rffj6QmSdSy+cBIuOy0EwrvY0X4oc0lz/8G8At0DzmP6XBCAd4WgiNLrmsywzDIyLWzJyOXvRl57D2Sx55j34vun67wBoitFeQZbn7iV6PIEAL99bdWpCKoKJfTyz4IS191F+RFs4NGNIQLhkCXO47PBmov+Qf9QGY+L36/kS9W7sEwINDPyt0XNWPoJc2JCNIMmiJVwTAM8hx5ZBRkkJGfwcHsg6wqXEXO5hzynHnFi+pTFNd5jrwKzWTBQmhAKCEBIYQFhBEWEEZoQChhgWElCu+igrtOcB1CAkIqNIeIlJ1hGKw+uJq5u+Yyd8dcjhYc9TwWXyueq5tfzZXNrqRBmJdessvldF8HvKgALyrCsw+cfP2QOu4e75j2x4vwui3BzzvexzhdBmlZ+acsuPdm5JFnP/Uw8yJ1QgM9vdwnfjWtE0pwoF8V/CQiNZuKcjm5rFT3+eLL3oWiN+Qx7aH7g9D2H6f9Z5Rb6ODthduYumib5x/B1R0bMPLyVsRF6U21yNlwupwcLTzKkfwjpOenc6TA/T0jP8Nz+0jBETLyMzy3C5wnuczMsrLv29/qT3hAuKeADg0I9Xz9vbg+3WPB/sHqyRbxIYXOQv5I+4Ofd//MrKxZZKQcn7uhbnBdrmx2JVfFX0XrqNbedTpaQZZ7uPmJBXja+uPva4qxQJ3mx4edFxXg4bFg4s9U4HCy/0i+p8De4ym4c9l7JI/9R/JxuE4znfkx9cJtNKwdTMPIYBod+97whO/h6iwRMZWKcikucx8seQVWvA+OY+dwNugCvR+HhKTT/mNyGfDFyr28/MMWz7UmuzSuzZNXtaFLY+8b0iXiDfId+cUK66Ie7ZPdPpJ/hCMFRzznapaFzc9GZFAktQNrU5hVSNPYpoQHhh8vnANPKJxPLK79QwkNdC/T+dciNYNhGGw7uo2l+5aydN9SlqcuLzavQ4h/CH2a9KFffD+6xXTDz2pyT6qjAI7sdl9+7MBf7pnPU/+CjO0nXz8gxD3c/MQCPLoNBIZWbW7c53N7iuxiRbf7+8HsgtNeQgzc53bH1go6SdEdQsPIYGJrBREUoN5uEW+molzcMna4e8ZXfuC5fAeNzoNej0OLy05bjGcXOFiy+SAvrvFj769rAYiLCubxvudwZfsY7/rUXKSSuAwXufZcz3Dwo4VHT1lcn3i7vEPDIwIjiAyKJNIWSe2g2kQFRRFpi3QvO7b8xNvB/sFYLBb35WXmzOHKi68kIEA9IyLilpqTyrLUZfye+jtL9y0tdvkygHrB9bgg5gJCDoTw4FUPEhEcUbUB8zIgfbv7/UrG9hNu74Cje+BUH1aGN/jb5GvtIaoZVMEHCfl2JwezCkjLKmBfRg7z91lY8e0G9mcWlPp8bgCbv9XTo93ohB7uRpEhNKwdTHREEH6aVE3Ep6kor8kKsmH9N7DqY9jx8/HljS+EXo9BfO8SxXi+3cm6/Zn8uecoq/ccYc2eo2w9mH3sU1wL4UH+PHBpC+7s3hSbvz6VFe9md9k9hXTRhGRFRXWxL0eOe5Zwh/t+0cRlJ66f68gtdw5/q//JC+pTFNm1bLUIsKqgFpHyMQyDPdl7WJ66nBUHVrD8wHL2Zu8tto7Nz8a50efSvUF3ujfoTovaLTyXBQz2D674UC6ne7ResYL7hNv5R07//IAQiIo/1vN9QgEeWqdCYxqGQWaeg7SsfNKyCo4V3fmkZRZwMLuAtEz3/YNZBWTm/31iSz/YWfLSaRFB/jQ8VmA3+tuw8oaRwdQJ1SXERKo7FeU1jcsFu5bCqhmw9v+OT96GxV2EX/wINL0ILBYMw2D34VyW70xn+c4MVu06wqYDWSc9dym2VhAtg3OZOPAiomtX/fAvqTkcLgfZhdmk56az37GfFWkrKDQKz1xYn/BVNJP4Sc+1Pkv+Fn9CAkKICIwgKiiK2kG1ibRFFrtdVFxH2dzLwgLC9IZLRCqN3WlnU8Ym1hxaw+qDq1meupwDucUnNvOz+HFO1Dl0jenKhQ0upEv9LgT5B1VskMLc473bfy++j+w6PlLvVMKiIbIpRDZz93afeDu03lmd++1wujiUXegpqNOyCo4V2vnHCm13AX4wu4BCh6vU2w30s1Iv3Ea98EAsuRmce048jeuE6nxuESlGRXlNYBhwcIO7CF89w/2Pr0hUPHQcAB1vxhHeiHX7M1m+ZIe7EN+R4Tk3/ER1wwLp0Kg27RvWomNcLdo3rE3tICtz5swhKlTnnMqpGYZBvjOf7MJssgqzyCzMJNvuvn3iV7Y9m8zCTPftY+tm2d2PlRju/cPZ5wq0BhIWGEaIf0ixCcpO9lU0Y3hoQCgh/iGe865DAtzPtfnZVGCLiGkMw2Bfzj7+PPgnqw+u5s9Df7L+8PpilysD9widdnXacW70uXSN6Urn+p0JDTjLD9UNA3IOnbq3Ozv19M+3BkDtxu5iO6rZ34rvpuU65zunwFGsR7t4wV1AWqZ7WXpu4RnP3T5RRJA/9SOCqBdmo36EjfrhNuqF26gfHlTsdkSwf/FThy5vqVOHRKQEFeXVVUEWbFsAm1Ngy4+Quef4Y7YIaPsPjI63ssXWloWbD7Hoq1SW71hHbmHxy2YE+Flo17AWXZtE0qVxJB3iatOgVlCJosN+kkuiSfXjMlyeIjq70F04ZxdmewrmkxXWnqL6WGHtcJX/OtUnCvILwt/lT1RY1PHZvo9NShbqf5IC+m+3iyY0CwkI0VBwEfFJTpeTnZk72ZC+gQ0ZG9iUvon16etJz08vsW5EYATt67anfb32nBt9Lh3rdSzXMHSL4YD0bZC1p+S53Rk7oDD79Buw1YKopu6C+8TiO7Ip1Gp02nO9XS6DrAIHR3PtHMkr5EiunSN5do7mum8fzinkYHYBB08YQp5TeObLgRXxs1qoGxboKaj/XnDXO6Hg1sRpIlKRVJRXFy4XHFx/rAj/AXb9AicWP/5B0PRiclvfwEJrNxZsy2bRjIPsP/pzsc1EBPlzbpNIujaNomuTSDrG1dY/Hh/kdDkpcBaQ68glz5FHviOfPEdeidsnfhVbx5nvfq49jyz78d7qHHtOuWb+/jurxUpYQBjhgeHHvwLCCQsMIyIwgrDAMMIDwos9HhYYRkSA+7GwwDBw4u51uFITlolI9WYYBofyDrHt6Da2Hd3GxvSNbEzfyOYjm096Go6/xZ9WUa1oX7c9Hep1oH3d9jSJaHLmUTwF2e7rdWfth8z9kLn32O19kLUf/8x9XJW5H+uq0w3ftkBEw2MFd9OSxXdwJE4DsvLtnqL6SG4hR3bYOZK769h9O0eLlufZjxXh7vuluPpXCcEBfiV6s+t5bh+/HxUaqAnTRMQUKsp9kT0f0tadcN3NY5f+8Jwf7uao3YyD0RezLrQbv7jasGJfHqu/PILLWO9Zx+Zv5fxmUfRqWY+LEurSsn44Vv1DqlQOl4NCZyF2l52c/BzSnelsObIFO/ZyFc35zpIFd2WcK30im5+tWDFdVDSfeN9TSAdGlCjAQ/xDznqIt92p0RkiUr3YnXb25exjx9EdngJ829FtbD+ynSx71kmfE+wfTMvIlrSOau353iqqFTY/m/sD+/wjkJ0GOxZDThpkH4ScgyVv5xwC++knrLQc+zL8g7BENsVVuykF4Y3JDo37//buPiqqOv8D+PveO48MDz6APCwqroaVGB6hTcwEy3R7Mrc9m7Wd0mOdXTctXF1aa9uD+qvAnta2o627W+runhPtOaXbgxpsAVpuZSimYlQ+pQkiCoIiMMx8fn/AXBlmQOaKDuL7xbln7v3eL3e+9zMzfPjce2cGtdZ4nLDEoFKJxskm9dwZ7KNO1HznxKmGs6g9uxO1DU7UNToDulTcZ5/NGvqFmBFhN6NfiBn97JbW2xBLu0K7regOtyHUyn93iah3uyz+Sq1cuRIvvPACKioqMGrUKCxfvhw33XRTsId1cblaWo9Q1x5qfQ94zaHWy8SO7QGOlwPiezmWU7XiO/sYbMEYrDs9CnsrIwH97VsVer+rBoViYmIUJiZG4YZhA66IM+GeM8dOtxPNrmY0uZrQ7G6G0+VsnXc1o9nd3Hrbcb7DcvvtdOzX8T78zbv8PHbYcHH2W4ECm8kGu8muTzbNBru53bxnndkOu9auX9vveZ2tbiuu+X3VRHQx9PV873K7cLLxJCrOVOBI/REcOX3E6/ZYwzG4xf9ZaFVREe+IwzBHLBJDYjDSMhAjtVAMdgm0xlrg5Engh3ygIe9cwd1Q7X3VXDe0aHY0WAeh3hKFWlMUarSBOK4MxDHph6Oufth10oRqUxxqj7tQf7jjtmvapu5xWDT0C/EU1K3FdUSIGf3s/pYt6B9iRrjdfEX830JEV5ZeX5S/9dZbmD9/PlauXIkbb7wRq1atwm233YaysjIMGTIk2MMLnMvZejT6zHGvyV1/DC11VXDXHoZ66jDMZ45C8Ve8talFGHa5hqJMhmKPOwFlMhQHJBauhnOJSlWAoQMdGB7lwPCoUFwVHYbxwwcirl/PfZWJiMAlrQVvozSiprEG0ixwup3nJpf3fLO72e+8v/6eM8od5736td16imx/2/FbCPcCqqJCEw2h1tb3NutFsrlDwdxhal9oe+ZDTCE+7TbN9/3/RES90eWa793iRl1THWqbanGq+RRONZ3CibMncPzscVQ1VKGqoQrHzxxD1dkqnGg8CVcnRbeHDSqGKFYMEw3DnC4kNDVi+NnTSGiogc190NAY65VQ1CAC1YhAlTscx9zhqHaHoxoRqJYInJBwHG+bPwsbcOY8G2zwvhorzGbyOmPtOYPdP8TSNm85V2iHmBFhb223mFRD+0NE1Nf0+qL85ZdfxsMPP4xHHnkEALB8+XJ8+OGHeO2115CTk3NJx5K38XmcOl0JcbdAcTshblfrEWi3s7VNXFDczYCrEaqrCZq7Caq7Caq7GZo0Q3M3wyxNEAVwQ4EAEABuAKIAAqV1XgVc4SFwioYaOHAKIahtu62WMBxHBM7AAkUBNFXgsNYhxLoHiZa9CLNrCLOqcNhU2C0qADdc4sJxcaPylAvFJa3L+uR2wS1utEgL3O7WdS3SApe7dX2Lu0Xv51lu39Yi3kfJn3nnmUv6mBihKiqsmhVm1QyLZvGat6iW1tu2qbN+Vs0Ki2aBWTX7ne+4Ha/ldvPiEr4vmogIvSff//fzN7HnyNbWtwS5m9AkTWh0N6PJ3YRGcaIJTpwVJ05LM+qVFpyBCxLAsU9VBJEuFwY7WxDf0jY5z90OdLvR1eYaxYxahKJGQlErYahBKGolFDUIRY2EoRahqJZwVEtbwY0IODv5d09RgFCLCQ6rCQ6rhkSrCSEWE8JsJoTaTAizmhBmMyPUZkKo1QS7SUH57lJMnpiGyDA7+oVYEG4zwaSxuCYiuhC9uihvbm5GSUkJFi1a5NU+ZcoUbN261e/vNDU1oanp3BHcuro6AK2fDn6+Twj3rO+s35tH/on9nV2168lHGgC/tZWlbQrtcgz+NbVN5z5N1dpubWPbdNIF4HTbFEQmxQSTatILVbNq9r+sti1rZr1dnzq0WTQLTKqpdV5ttx3N5L3c4X7ab8dTVJvU3vG0F5ec9zlHnWPsjGHcjOvJ2DH+3gLN9xeS6z392t+2t3HXP5BvPuLT7sXz5up2HG43+rnciHC70N/lxiCXC1EtLgxytU0tLjhaNNhcZjSJDadhx2nYcUZsOAMbysSObbDjDGyoEwdOiQOn4ECDFoYmLRyN5jA0m8KhWuywmTXYzSrsFg12s9a2rMFu0RBrVvFji4YQiwkhZg0hlnOTve3WYWktwu1mLaCrqZxOJ0w/CJJiHPqBZHG74HT3zqvRehP+7TWGcTOGcTMuWLm+d1QnnaiurobL5UJ0dLRXe3R0NCor/X/XZU5ODpYsWeLTnp+fj5CQkG7db0FBgd/2SGcENPdpSFsF3nrbmplFv1UhigqB1jopKkQ5Nw/FDCgmaKoKDYCmKNBUBRoUaAqgKSoUz4+ioOOPClVf55nX26BAVc616esV1aevp81fP/1HUaFB81rvWfaab7esQYOqdHHEXAC42qYL5Gr7acLF/VCzS6Gz5xydH2NnDONmXE/ErqGh6w/UutIEmu97ItcD/h9LW3N/JDsrYXFrsIgKs2itk1uDSUwwixkmMcMsNljEDpPYoUkoRLHBqVjgUi1oUSxo0ayoUa2oMtvgUq0Q1QJNU9tyPWBRAZMKmFWBSQVMCmBWgQEqEK22zpuU1rPZ53gO0nfCk18bvZvq26aewr8fxjF2xjBuxjBuxl3qXN+ri3KPjkdxRaTTI7tPPvkkFixYoC/X1dVh8ODBmDJlCsLDw7u8H6fTiYKCAtx6661+LyW+HbcbGP2V4XyxI/8YN+MYO2MYN+N6MnaeM7vkrbv5/kJyPdD1Y8lc3zn+/TCOsTOGcTOGcTMuWLm+VxflkZGR0DTN5yh5VVWVz9F0D6vVCqvV6tNuNpu7HdhA+pI3xs4Yxs04xs4Yxs24nogdY+8t0HzfE7neSH9qxbgZx9gZw7gZw7gZd6lzfa/+ZA6LxYKUlBSfywcKCgowfvz4II2KiIiIehLzPRERXcl69ZlyAFiwYAEefPBBpKamIi0tDX/961/x/fffY86cOcEeGhEREfUQ5nsiIrpS9fqifMaMGThx4gSWLl2KiooKJCUlYcOGDRg6dGiwh0ZEREQ9hPmeiIiuVL2+KAeARx99FI8++miwh0FEREQXEfM9ERFdiXr1e8qJiIiIiIiI+jIW5URERERERERBwqKciIiIiIiIKEhYlBMREREREREFCYtyIiIiIiIioiBhUU5EREREREQUJJfFV6JdCBEBANTV1Z23r9PpRENDA+rq6mA2my/20PoUxs4Yxs04xs4Yxs24noydJyd5chRdmEByPcDXgVGMm3GMnTGMmzGMm3HByvV9viivr68HAAwePDjIIyEiIvJWX1+PiIiIYA/jssdcT0REvVV3cr0iffwwvdvtxtGjRxEWFgZFUbrsW1dXh8GDB+Pw4cMIDw+/RCPsGxg7Yxg34xg7Yxg343oydiKC+vp6xMXFQVX5TrILFUiuB/g6MIpxM46xM4ZxM4ZxMy5Yub7PnylXVRXx8fEB/U54eDifwAYxdsYwbsYxdsYwbsb1VOx4hrznGMn1AF8HRjFuxjF2xjBuxjBuxl3qXM/D80RERERERERBwqKciIiIiIiIKEhYlLdjtVqRnZ0Nq9Ua7KFcdhg7Yxg34xg7Yxg34xi7voOPpTGMm3GMnTGMmzGMm3HBil2f/6A3IiIiIiIiot6KZ8qJiIiIiIiIgoRFOREREREREVGQsCgnIiIiIiIiChIW5URERERERERBwqK8nZUrV2LYsGGw2WxISUnBli1bgj2koNq8eTPuuusuxMXFQVEUrF+/3mu9iGDx4sWIi4uD3W5HRkYG9uzZ49WnqakJjz32GCIjI+FwODBt2jQcOXLkEu7FpZeTk4Prr78eYWFhGDRoEKZPn47y8nKvPoydr9deew3XXXcdwsPDER4ejrS0NGzcuFFfz5h1T05ODhRFwfz58/U2xs6/xYsXQ1EUrykmJkZfz7j1Tcz13pjrjWGuN475vmcw33ffZZHvhUREJC8vT8xms/ztb3+TsrIyyczMFIfDIYcOHQr20IJmw4YN8oc//EHefvttASDr1q3zWp+bmythYWHy9ttvy65du2TGjBkSGxsrdXV1ep85c+bIj370IykoKJDt27fLpEmTJDk5WVpaWi7x3lw6U6dOldWrV8vu3bultLRU7rjjDhkyZIicPn1a78PY+Xr33Xflgw8+kPLycikvL5ennnpKzGaz7N69W0QYs+744osvJCEhQa677jrJzMzU2xk7/7Kzs2XUqFFSUVGhT1VVVfp6xq3vYa73xVxvDHO9ccz3F475PjCXQ75nUd7mJz/5icyZM8er7eqrr5ZFixYFaUS9S8dE7Xa7JSYmRnJzc/W2xsZGiYiIkL/85S8iIlJbWytms1ny8vL0Pj/88IOoqiqbNm26ZGMPtqqqKgEgxcXFIsLYBaJ///7y97//nTHrhvr6ernqqqukoKBA0tPT9STN2HUuOztbkpOT/a5j3Pom5vquMdcbx1x/YZjvu4/5PnCXQ77n5esAmpubUVJSgilTpni1T5kyBVu3bg3SqHq3AwcOoLKy0itmVqsV6enpesxKSkrgdDq9+sTFxSEpKemKiuupU6cAAAMGDADA2HWHy+VCXl4ezpw5g7S0NMasG+bOnYs77rgDkydP9mpn7Lr27bffIi4uDsOGDcN9992H/fv3A2Dc+iLm+sDxddB9zPXGMN8HjvnemN6e7009spXLXHV1NVwuF6Kjo73ao6OjUVlZGaRR9W6euPiL2aFDh/Q+FosF/fv39+lzpcRVRLBgwQJMmDABSUlJABi7ruzatQtpaWlobGxEaGgo1q1bh2uvvVb/g8eY+ZeXl4ft27dj27ZtPuv4fOvcDTfcgH/84x9ITEzEsWPH8Mwzz2D8+PHYs2cP49YHMdcHjq+D7mGuDxzzvTHM98ZcDvmeRXk7iqJ4LYuITxt5MxKzKymu8+bNw1dffYVPPvnEZx1j52vkyJEoLS1FbW0t3n77bcycORPFxcX6esbM1+HDh5GZmYn8/HzYbLZO+zF2vm677TZ9fvTo0UhLS8Pw4cOxdu1ajBs3DgDj1hcx1weOr4OuMdcHjvk+cMz3xl0O+Z6XrwOIjIyEpmk+Rzqqqqp8jppQK88nFnYVs5iYGDQ3N6OmpqbTPn3ZY489hnfffReFhYWIj4/X2xm7zlksFowYMQKpqanIyclBcnIyXnnlFcasCyUlJaiqqkJKSgpMJhNMJhOKi4vx5z//GSaTSd93xu78HA4HRo8ejW+//ZbPuT6IuT5wfB2cH3O9Mcz3gWO+7zm9Md+zKEfrH4aUlBQUFBR4tRcUFGD8+PFBGlXvNmzYMMTExHjFrLm5GcXFxXrMUlJSYDabvfpUVFRg9+7dfTquIoJ58+bhnXfewccff4xhw4Z5rWfsuk9E0NTUxJh14ZZbbsGuXbtQWlqqT6mpqXjggQdQWlqKH//4x4xdNzU1NWHv3r2IjY3lc64PYq4PHF8HnWOu71nM9+fHfN9zemW+75GPi+sDPF+T8vrrr0tZWZnMnz9fHA6HHDx4MNhDC5r6+nrZsWOH7NixQwDIyy+/LDt27NC/OiY3N1ciIiLknXfekV27dsn999/v9+sD4uPj5b///a9s375dbr755j7/tQu/+c1vJCIiQoqKiry+eqGhoUHvw9j5evLJJ2Xz5s1y4MAB+eqrr+Spp54SVVUlPz9fRBizQLT/NFYRxq4zCxculKKiItm/f7989tlncuedd0pYWJj+d59x63uY630x1xvDXG8c833PYb7vnssh37Mob2fFihUydOhQsVgsMnbsWP1rLa5UhYWFAsBnmjlzpoi0foVAdna2xMTEiNVqlYkTJ8quXbu8tnH27FmZN2+eDBgwQOx2u9x5553y/fffB2FvLh1/MQMgq1ev1vswdr5mz56tv/6ioqLklltu0RO0CGMWiI5JmrHzz/M9pGazWeLi4uSee+6RPXv26OsZt76Jud4bc70xzPXGMd/3HOb77rkc8r0iItIz59yJiIiIiIiIKBB8TzkRERERERFRkLAoJyIiIiIiIgoSFuVEREREREREQcKinIiIiIiIiChIWJQTERERERERBQmLciIiIiIiIqIgYVFOREREREREFCQsyokukoMHD0JRFJSWlgZ7KLqvv/4a48aNg81mw5gxYy54e2vWrEG/fv0ueDsZGRmYP3/+BW+nuxYvXnze/Z81axamT59+ScZDRESXJ+b67mOuJ+oci3Lqs2bNmgVFUZCbm+vVvn79eiiKEqRRBVd2djYcDgfKy8vx0UcfXfD2ZsyYgW+++aYHRta17iTWnvbKK69gzZo1l/Q+iYgoMMz1vpjru4+5nnoLFuXUp9lsNixbtgw1NTXBHkqPaW5uNvy7+/btw4QJEzB06FAMHDjwgsdit9sxaNCgC97OpSIiaGlp6VbfiIiIHjkzQEREFxdzvTfmeuZ6uvywKKc+bfLkyYiJiUFOTk6nffwdmV2+fDkSEhL0Zc/lTc899xyio6PRr18/LFmyBC0tLcjKysKAAQMQHx+PN954w2f7X3/9NcaPHw+bzYZRo0ahqKjIa31ZWRluv/12hIaGIjo6Gg8++CCqq6v19RkZGZg3bx4WLFiAyMhI3HrrrX73w+12Y+nSpYiPj4fVasWYMWOwadMmfb2iKCgpKcHSpUuhKAoWL17ss4333nsP/fr1g9vtBgCUlpZCURRkZWXpfX7961/j/vvvB+B7SZsnlv/85z+RkJCAiIgI3Hfffaivr9f7nDlzBg899BBCQ0MRGxuLl156ye/+eKxZswZLlizBzp07oSgKFEXBmjVr/F4yWFtbC0VR9BgXFRVBURR8+OGHSE1NhdVqxZYtW/T+q1atwuDBgxESEoJf/OIXqK2t1dd1vKQtIyMDjz/+OJ544gkMGDAAMTExPjE8deoUfvWrX2HQoEEIDw/HzTffjJ07d+rrd+7ciUmTJiEsLAzh4eFISUnBl19+2eX+ExFR15jrmeuZ6+lyx6Kc+jRN0/Dcc8/h1VdfxZEjRy5oWx9//DGOHj2KzZs34+WXX8bixYtx5513on///vj8888xZ84czJkzB4cPH/b6vaysLCxcuBA7duzA+PHjMW3aNJw4cQIAUFFRgfT0dIwZMwZffvklNm3ahGPHjuHee+/12sbatWthMpnw6aefYtWqVX7H98orr+Cll17Ciy++iK+++gpTp07FtGnT8O233+r3NWrUKCxcuBAVFRX43e9+57ONiRMnor6+Hjt27AAAFBcXIzIyEsXFxXqfoqIipKendxqnffv2Yf369Xj//ffx/vvvo7i42OuywqysLBQWFmLdunXIz89HUVERSkpKOt3ejBkzsHDhQowaNQoVFRWoqKjAjBkzOu3vzxNPPIGcnBzs3bsX1113HQDgu+++w7///W+899572LRpE0pLSzF37twut7N27Vo4HA58/vnneP7557F06VIUFBQAaD0yf8cdd6CyshIbNmxASUkJxo4di1tuuQUnT54EADzwwAOIj4/Htm3bUFJSgkWLFsFsNge0L0RE5I25nrkeYK6ny5wQ9VEzZ86Uu+++W0RExo0bJ7NnzxYRkXXr1kn7p352drYkJyd7/e6f/vQnGTp0qNe2hg4dKi6XS28bOXKk3HTTTfpyS0uLOBwOefPNN0VE5MCBAwJAcnNz9T5Op1Pi4+Nl2bJlIiLyxz/+UaZMmeJ134cPHxYAUl5eLiIi6enpMmbMmPPub1xcnDz77LNebddff708+uij+nJycrJkZ2d3uZ2xY8fKiy++KCIi06dPl2effVYsFovU1dVJRUWFAJC9e/eKiMjq1aslIiJC/93s7GwJCQmRuro6vS0rK0tuuOEGERGpr68Xi8UieXl5+voTJ06I3W6XzMzMTsfk7zHyxHfHjh16W01NjQCQwsJCEREpLCwUALJ+/Xqf7WmaJocPH9bbNm7cKKqqSkVFhYh4P39EWh+HCRMmeG3n+uuvl9///vciIvLRRx9JeHi4NDY2evUZPny4rFq1SkREwsLCZM2aNZ3uJxERBYa5nrmeuZ76Ap4ppyvCsmXLsHbtWpSVlRnexqhRo6Cq514y0dHRGD16tL6saRoGDhyIqqoqr99LS0vT500mE1JTU7F3714AQElJCQoLCxEaGqpPV199NYDWo9AeqampXY6trq4OR48exY033ujVfuONN+r31V0ZGRkoKiqCiGDLli24++67kZSUhE8++QSFhYWIjo7Wx+hPQkICwsLC9OXY2Fg9Jvv27UNzc7NXTAYMGICRI0cGNMZA+YvfkCFDEB8fry+npaXB7XajvLy80+14jrx7tN+3kpISnD59GgMHDvR6PA8cOKA/lgsWLMAjjzyCyZMnIzc31+sxJiKiC8Nc333M9cz11LuYgj0Aokth4sSJmDp1Kp566inMmjXLa52qqhARrzan0+mzjY6XHimK4rfN8x6trng+EdbtduOuu+7CsmXLfPrExsbq8w6H47zbbL9dDxEJ+NNnMzIy8Prrr2Pnzp1QVRXXXnst0tPTUVxcjJqami4vZwP8x8kTk45xvhCef5rab9Pf4wZ0L36eOHUVr672ze12IzY21ud9hAD09+ItXrwYv/zlL/HBBx9g48aNyM7ORl5eHn72s5+dd3xERNQ15vruY65nrqfehWfK6YqRm5uL9957D1u3bvVqj4qKQmVlpdcf/J78vtHPPvtMn29paUFJSYl+9Hns2LHYs2cPEhISMGLECK+pu8kZAMLDwxEXF4dPPvnEq33r1q245pprAhqv571my5cvR3p6OhRFQXp6OoqKis77HrPzGTFiBMxms1dMampqzvtVKxaLBS6Xy6stKioKQOv75zwCedy+//57HD16VF/+3//+B1VVkZiY2O1ttDd27FhUVlbCZDL5PJaRkZF6v8TERPz2t79Ffn4+7rnnHqxevdrQ/RERkS/m+u5hrmeup96FRTldMUaPHo0HHngAr776qld7RkYGjh8/jueffx779u3DihUrsHHjxh673xUrVmDdunX4+uuvMXfuXNTU1GD27NkAgLlz5+LkyZO4//778cUXX2D//v3Iz8/H7NmzfRLT+WRlZWHZsmV46623UF5ejkWLFqG0tBSZmZkBbSciIgJjxozBv/71L2RkZABoTd7bt2/HN998o7cZERoaiocffhhZWVn46KOPsHv3bsyaNcvrUkF/EhIScODAAZSWlqK6uhpNTU2w2+0YN24ccnNzUVZWhs2bN+Ppp5/u9lhsNhtmzpyJnTt3YsuWLXj88cdx7733IiYmxtC+TZ48GWlpaZg+fTo+/PBDHDx4EFu3bsXTTz+NL7/8EmfPnsW8efNQVFSEQ4cO4dNPP8W2bdsC/keKiIg6x1zfPcz1zPXUu7AopyvK//3f//lcVnXNNddg5cqVWLFiBZKTk/HFF1/4/bRSo3Jzc7Fs2TIkJydjy5Yt+M9//qMfTY2Li8Onn34Kl8uFqVOnIikpCZmZmYiIiDhv8uro8ccfx8KFC7Fw4UKMHj0amzZtwrvvvourrroq4DFPmjQJLpdLT8r9+/fHtddei6ioqAtOLC+88AImTpyIadOmYfLkyZgwYQJSUlK6/J2f//zn+OlPf4pJkyYhKioKb775JgDgjTfegNPpRGpqKjIzM/HMM890exwjRozAPffcg9tvvx1TpkxBUlISVq5caXi/FEXBhg0bMHHiRMyePRuJiYm47777cPDgQURHR0PTNJw4cQIPPfQQEhMTce+99+K2227DkiVLDN8nERH5Yq7vHub6wDHX08WiSE++8YOIiIiIiIiIuo1nyomIiIiIiIiChEU5ERERERERUZCwKCciIiIiIiIKEhblREREREREREHCopyIiIiIiIgoSFiUExEREREREQUJi3IiIiIiIiKiIGFRTkRERERERBQkLMqJiIiIiIiIgoRFOREREREREVGQsCgnIiIiIiIiChIW5URERERERERB8v+SboA2oWbXqwAAAABJRU5ErkJggg==\n",
                        "text/plain": [
                            "<Figure size 1200x400 with 2 Axes>"
                        ]
                    },
                    "metadata": {},
                    "output_type": "display_data"
                }
            ],
            "source": [
                "data = {\n",
                "    \"fd\":((10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 150,200, 250, 300),\n",
                "          [0.89, 3.06, 7.13, 14.77, 24.46, 41.06, 64.46, 105.98, 140.76, 171.53, 590.46, 1501.62, 2957.65, 4904.31],\n",
                "          [14.1, 31.9, 58.8, 92.2, 135.3, 184.2, 240.6, 303.1, 373.6, 450.7, 946.5, 1620.8, 2470.1, 3500.5]),   \n",
                "\"cs\":((10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 150, 200, 250),\n",
                "      [1.18, 4.9, 12.44, 25.58, 44.56, 72.82, 115.46, 171.42, 245.15, 312.9, 960.64, 2883.04, 5345.27],\n",
                "      [22.3, 55.7, 107.6, 171.0, 244.1, 338.7, 442.7, 566.9, 690.9, 839.0, 1787.4, 3088.9, 4742.4]),\n",
                "\"autograd\":((10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 150, 200, 250, 300, 350, 400, 450, 500),\n",
                "            [0.32, 0.78, 1.52, 2.49, 3.75, 5.33, 7.14, 9.12, 11.43, 14.02, 32.35, 53.73, 84.94, 130.53, 169.34, 229.62, 270.19, 342.01],\n",
                "            [26.7, 92.9, 196.4, 340.0, 525.9, 749.6, 1011.1, 1312.2, 1656.0, 2039.7, 4555.0, 8066.8, 12569.9, 18072.6, 24568.2, 32069.6, 40558.9, 50036.6]),\n",
                "       }\n",
                "ax1,ax2 = plt.subplots(1,2, figsize=(12,4))[1]\n",
                "for k,(n,t,m) in data.items():\n",
                "    ax1.plot(n,np.array(t)/60, label=k)\n",
                "    ax2.plot(n,np.array(m)/1024, label=k)\n",
                "setup_plot(ax1, xlabel='Number of wind turbines', ylabel='Time [min]')\n",
                "setup_plot(ax2, xlabel='Number of wind turbines', ylabel='Memory usage [GB]')\n",
                "plt.savefig('test.png', dpi=600)\n",
                "import os\n",
                "os.getcwd()"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "d087399e",
            "metadata": {},
            "source": [
                "## Chunkify and Parallelization\n",
                "\n",
                "PyWake makes it easy to chunkify the run wind farm simulations see also section [Run Wind Farm Simulation](https://topfarm.pages.windenergy.dtu.dk/PyWake/notebooks/RunWindFarmSimulation.html).\n",
                "\n",
                "This construct is also available and usefull when computing gradients to reduce the memory usage and/or speed up the computation by parallel execution.\n",
                "\n",
                "The arguments, `wd_chunks`, `ws_chunks` and `n_cpu` are available in the `WindFarmModel.aep(...)`, `WindFarmModel(...)` and `WindFarmModel.aep_gradients(...)` methods.\n"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 23,
            "id": "da77d44a",
            "metadata": {},
            "outputs": [],
            "source": [
                "from py_wake import np\n",
                "import matplotlib.pyplot as plt\n",
                "\n",
                "from py_wake.deficit_models.noj import NOJ\n",
                "from py_wake.examples.data.hornsrev1 import Hornsrev1Site, HornsrevV80, wt_x, wt_y, wt16_x, wt16_y\n",
                "from py_wake.utils.profiling import timeit\n",
                "import multiprocessing\n",
                "from py_wake.utils.gradients import autograd, fd\n",
                "from py_wake.utils.plotting import setup_plot"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 24,
            "id": "e20ff75b",
            "metadata": {},
            "outputs": [],
            "source": [
                "site = Hornsrev1Site()\n",
                "wt = HornsrevV80()\n",
                "wfm = NOJ(site, wt)\n",
                "x,y = wt16_x,wt16_y"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "d52b3a61",
            "metadata": {},
            "source": [
                "### AEP\n",
                "\n",
                "Computing AEP in parallel chunks.\n",
                "\n",
                "Setting `n_cpu=None`, splits the problem into `N` wind direction chunks which is computed in parallel on `N` CPUs, where `N` is the number of CPUs on the machine. Alternatively, a number can be specified."
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 25,
            "id": "1f8af440",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "Total AEP: 143.151568 GWh\n"
                    ]
                }
            ],
            "source": [
                "print('Total AEP: %f GWh'%wfm.aep(x, y, n_cpu=None))"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "1679a383",
            "metadata": {},
            "source": [
                "### WS, TI, Power and custom functions\n",
                "\n",
                "Computing mean power in parallel chunks"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 27,
            "id": "52e571fa",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "Mean Power: 1.434559 MW\n"
                    ]
                }
            ],
            "source": [
                "def mean_power(x,y):\n",
                "    power_ilk = wfm(x=x, y=y, n_cpu=None, return_simulationResult=False)[2] # index 2 = power_ilk\n",
                "    return power_ilk.mean()\n",
                "\n",
                "print('Mean Power: %f MW'%(mean_power(x,y)/1e6))"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "6d97c071",
            "metadata": {},
            "source": [
                "### AEP gradients\n",
                "\n",
                "In the previous section, [Gradients of AEP](#Gradients-of-AEP), the `aep_gradients` method was used like this:"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "e8794831",
            "metadata": {},
            "source": [
                "```python\n",
                "gradient_function = wfm.aep_gradients(fd, wrt_arg='xy')\n",
                "daep = gradient_function(x=x,y=y)\n",
                "```"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "efe73a0a",
            "metadata": {},
            "source": [
                "When dealing with chunkification and/or parallelization, the `aep_gradients` must be used in a slightly different way:"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 29,
            "id": "5c5c8367",
            "metadata": {},
            "outputs": [],
            "source": [
                "daep = wfm.aep_gradients(autograd, wrt_arg=['x','y'], n_cpu=None, x=x, y=y)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "14d7dc9c",
            "metadata": {},
            "source": [
                "Note, in this case, the arguments normally passed to `wfm.aep` (here `x` and `y`) are passed directly to the `wfm.aep_gradients` method as keyword arguments and the method returns the gradients results instead of a function."
            ]
        },
        {
            "cell_type": "markdown",
            "id": "f29410f7",
            "metadata": {},
            "source": [
                "**The plot below shows the time it takes to compute the gradients of AEP with respect to x and y plotted as a function of number of wind turbines and CPUs**"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "23fb8d0f",
            "metadata": {},
            "source": [
                "    from py_wake.utils import layouts \n",
                "    from py_wake.utils.profiling import timeit\n",
                "    from tqdm.notebook import tqdm\n",
                "\n",
                "    n_lst = np.arange(100,600,100)\n",
                "\n",
                "    def run(n, n_cpu):\n",
                "        x,y = layouts.rectangle(n,20,5*wt.diameter())\n",
                "        return (n, n_cpu, np.mean(timeit(wfm.aep_gradients)(autograd, ['x','y'], n_cpu=n_cpu, x=x,y=y)[1]))\n",
                "\n",
                "    res = {f'{n_cpu} CPUs': np.array([run(n, n_cpu=n_cpu) for n in tqdm(n_lst)]) for n_cpu in [1, 4, 16, 32]}\n",
                "\n",
                "    ax1,ax2 = plt.subplots(1,2, figsize=(12,4))[1]\n",
                "    for k,v in res.items():\n",
                "        n,n_cpu,t = v.T\n",
                "        ax1.plot(n, t, label=k)\n",
                "        ax2.plot(n, res['1 CPUs'][:,2]/n_cpu/t*100, label=k)\n",
                "    setup_plot(ax=ax1,xlabel='No. wind turbines',ylabel='Time [s]')\n",
                "    setup_plot(ax=ax2,xlabel='No. wind turbines',ylabel='CPU utilization [%]')\n",
                "    plt.savefig('images/Optimization_time_cpuwt.svg')"
            ]
        },
        {
            "attachments": {
                "Optimization_time_cpuwt.svg": {
                    "image/svg+xml": [
                        "PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0idXRmLTgiIHN0YW5kYWxvbmU9Im5vIj8+CjwhRE9DVFlQRSBzdmcgUFVCTElDICItLy9XM0MvL0RURCBTVkcgMS4xLy9FTiIKICAiaHR0cDovL3d3dy53My5vcmcvR3JhcGhpY3MvU1ZHLzEuMS9EVEQvc3ZnMTEuZHRkIj4KPHN2ZyB4bWxuczp4bGluaz0iaHR0cDovL3d3dy53My5vcmcvMTk5OS94bGluayIgd2lkdGg9Ijg2NHB0IiBoZWlnaHQ9IjI4OHB0IiB2aWV3Qm94PSIwIDAgODY0IDI4OCIgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB2ZXJzaW9uPSIxLjEiPgogPG1ldGFkYXRhPgogIDxyZGY6UkRGIHhtbG5zOmRjPSJodHRwOi8vcHVybC5vcmcvZGMvZWxlbWVudHMvMS4xLyIgeG1sbnM6Y2M9Imh0dHA6Ly9jcmVhdGl2ZWNvbW1vbnMub3JnL25zIyIgeG1sbnM6cmRmPSJodHRwOi8vd3d3LnczLm9yZy8xOTk5LzAyLzIyLXJkZi1zeW50YXgtbnMjIj4KICAgPGNjOldvcms+CiAgICA8ZGM6dHlwZSByZGY6cmVzb3VyY2U9Imh0dHA6Ly9wdXJsLm9yZy9kYy9kY21pdHlwZS9TdGlsbEltYWdlIi8+CiAgICA8ZGM6ZGF0ZT4yMDIyLTA1LTA2VDExOjQ5OjI1LjMxMzUwOTwvZGM6ZGF0ZT4KICAgIDxkYzpmb3JtYXQ+aW1hZ2Uvc3ZnK3htbDwvZGM6Zm9ybWF0PgogICAgPGRjOmNyZWF0b3I+CiAgICAgPGNjOkFnZW50PgogICAgICA8ZGM6dGl0bGU+TWF0cGxvdGxpYiB2My41LjEsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvPC9kYzp0aXRsZT4KICAgICA8L2NjOkFnZW50PgogICAgPC9kYzpjcmVhdG9yPgogICA8L2NjOldvcms+CiAgPC9yZGY6UkRGPgogPC9tZXRhZGF0YT4KIDxkZWZzPgogIDxzdHlsZSB0eXBlPSJ0ZXh0L2NzcyI+KntzdHJva2UtbGluZWpvaW46IHJvdW5kOyBzdHJva2UtbGluZWNhcDogYnV0dH08L3N0eWxlPgogPC9kZWZzPgogPGcgaWQ9ImZpZ3VyZV8xIj4KICA8ZyBpZD0icGF0Y2hfMSI+CiAgIDxwYXRoIGQ9Ik0gMCAyODggCkwgODY0IDI4OCAKTCA4NjQgMCAKTCAwIDAgCkwgMCAyODggCnoKIiBzdHlsZT0iZmlsbDogbm9uZSIvPgogIDwvZz4KICA8ZyBpZD0iYXhlc18xIj4KICAgPGcgaWQ9InBhdGNoXzIiPgogICAgPHBhdGggZD0iTSAxMDggMjUyIApMIDQxMi4zNjM2MzYgMjUyIApMIDQxMi4zNjM2MzYgMzQuNTYgCkwgMTA4IDM0LjU2IAp6CiIgc3R5bGU9ImZpbGw6ICNmZmZmZmYiLz4KICAgPC9nPgogICA8ZyBpZD0ibWF0cGxvdGxpYi5heGlzXzEiPgogICAgPGcgaWQ9Inh0aWNrXzEiPgogICAgIDxnIGlkPSJsaW5lMmRfMSI+CiAgICAgIDxwYXRoIGQ9Ik0gMTIxLjgzNDcxMSAyNTIgCkwgMTIxLjgzNDcxMSAzNC41NiAKIiBjbGlwLXBhdGg9InVybCgjcDA2M2M4ZjVlYjgpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzIiPgogICAgICA8ZGVmcz4KICAgICAgIDxwYXRoIGlkPSJtNTgzYjZlNWY1OSIgZD0iTSAwIDAgCkwgMCAzLjUgCiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9kZWZzPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI201ODNiNmU1ZjU5IiB4PSIxMjEuODM0NzExIiB5PSIyNTIiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMSI+CiAgICAgIDwhLS0gMTAwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSgxMTIuMjkwOTYxIDI2Ni41OTg0Mzcpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDxkZWZzPgogICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTMxIiBkPSJNIDc5NCA1MzEgCkwgMTgyNSA1MzEgCkwgMTgyNSA0MDkxIApMIDcwMyAzODY2IApMIDcwMyA0NDQxIApMIDE4MTkgNDY2NiAKTCAyNDUwIDQ2NjYgCkwgMjQ1MCA1MzEgCkwgMzQ4MSA1MzEgCkwgMzQ4MSAwIApMIDc5NCAwIApMIDc5NCA1MzEgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTMwIiBkPSJNIDIwMzQgNDI1MCAKUSAxNTQ3IDQyNTAgMTMwMSAzNzcwIApRIDEwNTYgMzI5MSAxMDU2IDIzMjggClEgMTA1NiAxMzY5IDEzMDEgODg5IApRIDE1NDcgNDA5IDIwMzQgNDA5IApRIDI1MjUgNDA5IDI3NzAgODg5IApRIDMwMTYgMTM2OSAzMDE2IDIzMjggClEgMzAxNiAzMjkxIDI3NzAgMzc3MCAKUSAyNTI1IDQyNTAgMjAzNCA0MjUwIAp6Ck0gMjAzNCA0NzUwIApRIDI4MTkgNDc1MCAzMjMzIDQxMjkgClEgMzY0NyAzNTA5IDM2NDcgMjMyOCAKUSAzNjQ3IDExNTAgMzIzMyA1MjkgClEgMjgxOSAtOTEgMjAzNCAtOTEgClEgMTI1MCAtOTEgODM2IDUyOSAKUSA0MjIgMTE1MCA0MjIgMjMyOCAKUSA0MjIgMzUwOSA4MzYgNDEyOSAKUSAxMjUwIDQ3NTAgMjAzNCA0NzUwIAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDwvZGVmcz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzEiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9Inh0aWNrXzIiPgogICAgIDxnIGlkPSJsaW5lMmRfMyI+CiAgICAgIDxwYXRoIGQ9Ik0gMTU2LjQyMTQ4OCAyNTIgCkwgMTU2LjQyMTQ4OCAzNC41NiAKIiBjbGlwLXBhdGg9InVybCgjcDA2M2M4ZjVlYjgpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzQiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI201ODNiNmU1ZjU5IiB4PSIxNTYuNDIxNDg4IiB5PSIyNTIiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMiI+CiAgICAgIDwhLS0gMTUwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSgxNDYuODc3NzM4IDI2Ni41OTg0Mzcpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDxkZWZzPgogICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTM1IiBkPSJNIDY5MSA0NjY2IApMIDMxNjkgNDY2NiAKTCAzMTY5IDQxMzQgCkwgMTI2OSA0MTM0IApMIDEyNjkgMjk5MSAKUSAxNDA2IDMwMzggMTU0MyAzMDYxIApRIDE2ODEgMzA4NCAxODE5IDMwODQgClEgMjYwMCAzMDg0IDMwNTYgMjY1NiAKUSAzNTEzIDIyMjggMzUxMyAxNDk3IApRIDM1MTMgNzQ0IDMwNDQgMzI2IApRIDI1NzUgLTkxIDE3MjIgLTkxIApRIDE0MjggLTkxIDExMjMgLTQxIApRIDgxOSA5IDQ5NCAxMDkgCkwgNDk0IDc0NCAKUSA3NzUgNTkxIDEwNzUgNTE2IApRIDEzNzUgNDQxIDE3MDkgNDQxIApRIDIyNTAgNDQxIDI1NjUgNzI1IApRIDI4ODEgMTAwOSAyODgxIDE0OTcgClEgMjg4MSAxOTg0IDI1NjUgMjI2OCAKUSAyMjUwIDI1NTMgMTcwOSAyNTUzIApRIDE0NTYgMjU1MyAxMjA0IDI0OTcgClEgOTUzIDI0NDEgNjkxIDIzMjIgCkwgNjkxIDQ2NjYgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgPC9kZWZzPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMSIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zNSIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSIxMjcuMjQ2MDk0Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieHRpY2tfMyI+CiAgICAgPGcgaWQ9ImxpbmUyZF81Ij4KICAgICAgPHBhdGggZD0iTSAxOTEuMDA4MjY0IDI1MiAKTCAxOTEuMDA4MjY0IDM0LjU2IAoiIGNsaXAtcGF0aD0idXJsKCNwMDYzYzhmNWViOCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfNiI+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTU4M2I2ZTVmNTkiIHg9IjE5MS4wMDgyNjQiIHk9IjI1MiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8zIj4KICAgICAgPCEtLSAyMDAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDE4MS40NjQ1MTQgMjY2LjU5ODQzNylzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPGRlZnM+CiAgICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtMzIiIGQ9Ik0gMTIyOCA1MzEgCkwgMzQzMSA1MzEgCkwgMzQzMSAwIApMIDQ2OSAwIApMIDQ2OSA1MzEgClEgODI4IDkwMyAxNDQ4IDE1MjkgClEgMjA2OSAyMTU2IDIyMjggMjMzOCAKUSAyNTMxIDI2NzggMjY1MSAyOTE0IApRIDI3NzIgMzE1MCAyNzcyIDMzNzggClEgMjc3MiAzNzUwIDI1MTEgMzk4NCAKUSAyMjUwIDQyMTkgMTgzMSA0MjE5IApRIDE1MzQgNDIxOSAxMjA0IDQxMTYgClEgODc1IDQwMTMgNTAwIDM4MDMgCkwgNTAwIDQ0NDEgClEgODgxIDQ1OTQgMTIxMiA0NjcyIApRIDE1NDQgNDc1MCAxODE5IDQ3NTAgClEgMjU0NCA0NzUwIDI5NzUgNDM4NyAKUSAzNDA2IDQwMjUgMzQwNiAzNDE5IApRIDM0MDYgMzEzMSAzMjk4IDI4NzMgClEgMzE5MSAyNjE2IDI5MDYgMjI2NiAKUSAyODI4IDIxNzUgMjQwOSAxNzQyIApRIDE5OTEgMTMwOSAxMjI4IDUzMSAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8L2RlZnM+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMyIi8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ4dGlja180Ij4KICAgICA8ZyBpZD0ibGluZTJkXzciPgogICAgICA8cGF0aCBkPSJNIDIyNS41OTUwNDEgMjUyIApMIDIyNS41OTUwNDEgMzQuNTYgCiIgY2xpcC1wYXRoPSJ1cmwoI3AwNjNjOGY1ZWI4KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2IwYjBiMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgICA8L2c+CiAgICAgPGcgaWQ9ImxpbmUyZF84Ij4KICAgICAgPGc+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNtNTgzYjZlNWY1OSIgeD0iMjI1LjU5NTA0MSIgeT0iMjUyIiBzdHlsZT0ic3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuOCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgIDxnIGlkPSJ0ZXh0XzQiPgogICAgICA8IS0tIDI1MCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoMjE2LjA1MTI5MSAyNjYuNTk4NDM3KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMyIi8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM1IiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ4dGlja181Ij4KICAgICA8ZyBpZD0ibGluZTJkXzkiPgogICAgICA8cGF0aCBkPSJNIDI2MC4xODE4MTggMjUyIApMIDI2MC4xODE4MTggMzQuNTYgCiIgY2xpcC1wYXRoPSJ1cmwoI3AwNjNjOGY1ZWI4KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2IwYjBiMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgICA8L2c+CiAgICAgPGcgaWQ9ImxpbmUyZF8xMCI+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTU4M2I2ZTVmNTkiIHg9IjI2MC4xODE4MTgiIHk9IjI1MiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF81Ij4KICAgICAgPCEtLSAzMDAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDI1MC42MzgwNjggMjY2LjU5ODQzNylzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPGRlZnM+CiAgICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtMzMiIGQ9Ik0gMjU5NyAyNTE2IApRIDMwNTAgMjQxOSAzMzA0IDIxMTIgClEgMzU1OSAxODA2IDM1NTkgMTM1NiAKUSAzNTU5IDY2NiAzMDg0IDI4NyAKUSAyNjA5IC05MSAxNzM0IC05MSAKUSAxNDQxIC05MSAxMTMwIC0zMyAKUSA4MTkgMjUgNDg4IDE0MSAKTCA0ODggNzUwIApRIDc1MCA1OTcgMTA2MiA1MTkgClEgMTM3NSA0NDEgMTcxNiA0NDEgClEgMjMwOSA0NDEgMjYyMCA2NzUgClEgMjkzMSA5MDkgMjkzMSAxMzU2IApRIDI5MzEgMTc2OSAyNjQyIDIwMDEgClEgMjM1MyAyMjM0IDE4MzggMjIzNCAKTCAxMjk0IDIyMzQgCkwgMTI5NCAyNzUzIApMIDE4NjMgMjc1MyAKUSAyMzI4IDI3NTMgMjU3NSAyOTM5IApRIDI4MjIgMzEyNSAyODIyIDM0NzUgClEgMjgyMiAzODM0IDI1NjcgNDAyNiAKUSAyMzEzIDQyMTkgMTgzOCA0MjE5IApRIDE1NzggNDIxOSAxMjgxIDQxNjIgClEgOTg0IDQxMDYgNjI4IDM5ODggCkwgNjI4IDQ1NTAgClEgOTg4IDQ2NTAgMTMwMiA0NzAwIApRIDE2MTYgNDc1MCAxODk0IDQ3NTAgClEgMjYxMyA0NzUwIDMwMzEgNDQyMyAKUSAzNDUwIDQwOTcgMzQ1MCAzNTQxIApRIDM0NTAgMzE1MyAzMjI4IDI4ODYgClEgMzAwNiAyNjE5IDI1OTcgMjUxNiAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8L2RlZnM+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMzIi8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ4dGlja182Ij4KICAgICA8ZyBpZD0ibGluZTJkXzExIj4KICAgICAgPHBhdGggZD0iTSAyOTQuNzY4NTk1IDI1MiAKTCAyOTQuNzY4NTk1IDM0LjU2IAoiIGNsaXAtcGF0aD0idXJsKCNwMDYzYzhmNWViOCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfMTIiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI201ODNiNmU1ZjU5IiB4PSIyOTQuNzY4NTk1IiB5PSIyNTIiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfNiI+CiAgICAgIDwhLS0gMzUwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSgyODUuMjI0ODQ1IDI2Ni41OTg0Mzcpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzMiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzUiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9Inh0aWNrXzciPgogICAgIDxnIGlkPSJsaW5lMmRfMTMiPgogICAgICA8cGF0aCBkPSJNIDMyOS4zNTUzNzIgMjUyIApMIDMyOS4zNTUzNzIgMzQuNTYgCiIgY2xpcC1wYXRoPSJ1cmwoI3AwNjNjOGY1ZWI4KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2IwYjBiMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgICA8L2c+CiAgICAgPGcgaWQ9ImxpbmUyZF8xNCI+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTU4M2I2ZTVmNTkiIHg9IjMyOS4zNTUzNzIiIHk9IjI1MiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF83Ij4KICAgICAgPCEtLSA0MDAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDMxOS44MTE2MjIgMjY2LjU5ODQzNylzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPGRlZnM+CiAgICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtMzQiIGQ9Ik0gMjQxOSA0MTE2IApMIDgyNSAxNjI1IApMIDI0MTkgMTYyNSAKTCAyNDE5IDQxMTYgCnoKTSAyMjUzIDQ2NjYgCkwgMzA0NyA0NjY2IApMIDMwNDcgMTYyNSAKTCAzNzEzIDE2MjUgCkwgMzcxMyAxMTAwIApMIDMwNDcgMTEwMCAKTCAzMDQ3IDAgCkwgMjQxOSAwIApMIDI0MTkgMTEwMCAKTCAzMTMgMTEwMCAKTCAzMTMgMTcwOSAKTCAyMjUzIDQ2NjYgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgPC9kZWZzPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zNCIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSIxMjcuMjQ2MDk0Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieHRpY2tfOCI+CiAgICAgPGcgaWQ9ImxpbmUyZF8xNSI+CiAgICAgIDxwYXRoIGQ9Ik0gMzYzLjk0MjE0OSAyNTIgCkwgMzYzLjk0MjE0OSAzNC41NiAKIiBjbGlwLXBhdGg9InVybCgjcDA2M2M4ZjVlYjgpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzE2Ij4KICAgICAgPGc+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNtNTgzYjZlNWY1OSIgeD0iMzYzLjk0MjE0OSIgeT0iMjUyIiBzdHlsZT0ic3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuOCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgIDxnIGlkPSJ0ZXh0XzgiPgogICAgICA8IS0tIDQ1MCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoMzU0LjM5ODM5OSAyNjYuNTk4NDM3KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM0Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM1IiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ4dGlja185Ij4KICAgICA8ZyBpZD0ibGluZTJkXzE3Ij4KICAgICAgPHBhdGggZD0iTSAzOTguNTI4OTI2IDI1MiAKTCAzOTguNTI4OTI2IDM0LjU2IAoiIGNsaXAtcGF0aD0idXJsKCNwMDYzYzhmNWViOCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfMTgiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI201ODNiNmU1ZjU5IiB4PSIzOTguNTI4OTI2IiB5PSIyNTIiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfOSI+CiAgICAgIDwhLS0gNTAwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSgzODguOTg1MTc2IDI2Ni41OTg0Mzcpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzUiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9InRleHRfMTAiPgogICAgIDwhLS0gTm8uIHdpbmQgdHVyYmluZXMgLS0+CiAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoMjE2LjI4MzM4MSAyODAuMjc2NTYzKXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgIDxkZWZzPgogICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtNGUiIGQ9Ik0gNjI4IDQ2NjYgCkwgMTQ3OCA0NjY2IApMIDM1NDcgNzYzIApMIDM1NDcgNDY2NiAKTCA0MTU5IDQ2NjYgCkwgNDE1OSAwIApMIDMzMDkgMCAKTCAxMjQxIDM5MDMgCkwgMTI0MSAwIApMIDYyOCAwIApMIDYyOCA0NjY2IAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTZmIiBkPSJNIDE5NTkgMzA5NyAKUSAxNDk3IDMwOTcgMTIyOCAyNzM2IApRIDk1OSAyMzc1IDk1OSAxNzQ3IApRIDk1OSAxMTE5IDEyMjYgNzU4IApRIDE0OTQgMzk3IDE5NTkgMzk3IApRIDI0MTkgMzk3IDI2ODcgNzU5IApRIDI5NTYgMTEyMiAyOTU2IDE3NDcgClEgMjk1NiAyMzY5IDI2ODcgMjczMyAKUSAyNDE5IDMwOTcgMTk1OSAzMDk3IAp6Ck0gMTk1OSAzNTg0IApRIDI3MDkgMzU4NCAzMTM3IDMwOTYgClEgMzU2NiAyNjA5IDM1NjYgMTc0NyAKUSAzNTY2IDg4OCAzMTM3IDM5OCAKUSAyNzA5IC05MSAxOTU5IC05MSAKUSAxMjA2IC05MSA3NzkgMzk4IApRIDM1MyA4ODggMzUzIDE3NDcgClEgMzUzIDI2MDkgNzc5IDMwOTYgClEgMTIwNiAzNTg0IDE5NTkgMzU4NCAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8cGF0aCBpZD0iRGVqYVZ1U2Fucy0yZSIgZD0iTSA2ODQgNzk0IApMIDEzNDQgNzk0IApMIDEzNDQgMCAKTCA2ODQgMCAKTCA2ODQgNzk0IAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTIwIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtNzciIGQ9Ik0gMjY5IDM1MDAgCkwgODQ0IDM1MDAgCkwgMTU2MyA3NjkgCkwgMjI3OCAzNTAwIApMIDI5NTYgMzUwMCAKTCAzNjc1IDc2OSAKTCA0MzkxIDM1MDAgCkwgNDk2NiAzNTAwIApMIDQwNTAgMCAKTCAzMzcyIDAgCkwgMjYxOSAyODY5IApMIDE4NjMgMCAKTCAxMTg0IDAgCkwgMjY5IDM1MDAgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtNjkiIGQ9Ik0gNjAzIDM1MDAgCkwgMTE3OCAzNTAwIApMIDExNzggMCAKTCA2MDMgMCAKTCA2MDMgMzUwMCAKegpNIDYwMyA0ODYzIApMIDExNzggNDg2MyAKTCAxMTc4IDQxMzQgCkwgNjAzIDQxMzQgCkwgNjAzIDQ4NjMgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtNmUiIGQ9Ik0gMzUxMyAyMTEzIApMIDM1MTMgMCAKTCAyOTM4IDAgCkwgMjkzOCAyMDk0IApRIDI5MzggMjU5MSAyNzQ0IDI4MzcgClEgMjU1MCAzMDg0IDIxNjMgMzA4NCAKUSAxNjk3IDMwODQgMTQyOCAyNzg3IApRIDExNTkgMjQ5MSAxMTU5IDE5NzggCkwgMTE1OSAwIApMIDU4MSAwIApMIDU4MSAzNTAwIApMIDExNTkgMzUwMCAKTCAxMTU5IDI5NTYgClEgMTM2NiAzMjcyIDE2NDUgMzQyOCAKUSAxOTI1IDM1ODQgMjI5MSAzNTg0IApRIDI4OTQgMzU4NCAzMjAzIDMyMTEgClEgMzUxMyAyODM4IDM1MTMgMjExMyAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8cGF0aCBpZD0iRGVqYVZ1U2Fucy02NCIgZD0iTSAyOTA2IDI5NjkgCkwgMjkwNiA0ODYzIApMIDM0ODEgNDg2MyAKTCAzNDgxIDAgCkwgMjkwNiAwIApMIDI5MDYgNTI1IApRIDI3MjUgMjEzIDI0NDggNjEgClEgMjE3MiAtOTEgMTc4NCAtOTEgClEgMTE1MCAtOTEgNzUxIDQxNSAKUSAzNTMgOTIyIDM1MyAxNzQ3IApRIDM1MyAyNTcyIDc1MSAzMDc4IApRIDExNTAgMzU4NCAxNzg0IDM1ODQgClEgMjE3MiAzNTg0IDI0NDggMzQzMiAKUSAyNzI1IDMyODEgMjkwNiAyOTY5IAp6Ck0gOTQ3IDE3NDcgClEgOTQ3IDExMTMgMTIwOCA3NTIgClEgMTQ2OSAzOTEgMTkyNSAzOTEgClEgMjM4MSAzOTEgMjY0MyA3NTIgClEgMjkwNiAxMTEzIDI5MDYgMTc0NyAKUSAyOTA2IDIzODEgMjY0MyAyNzQyIApRIDIzODEgMzEwMyAxOTI1IDMxMDMgClEgMTQ2OSAzMTAzIDEyMDggMjc0MiAKUSA5NDcgMjM4MSA5NDcgMTc0NyAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8cGF0aCBpZD0iRGVqYVZ1U2Fucy03NCIgZD0iTSAxMTcyIDQ0OTQgCkwgMTE3MiAzNTAwIApMIDIzNTYgMzUwMCAKTCAyMzU2IDMwNTMgCkwgMTE3MiAzMDUzIApMIDExNzIgMTE1MyAKUSAxMTcyIDcyNSAxMjg5IDYwMyAKUSAxNDA2IDQ4MSAxNzY2IDQ4MSAKTCAyMzU2IDQ4MSAKTCAyMzU2IDAgCkwgMTc2NiAwIApRIDExMDAgMCA4NDcgMjQ4IApRIDU5NCA0OTcgNTk0IDExNTMgCkwgNTk0IDMwNTMgCkwgMTcyIDMwNTMgCkwgMTcyIDM1MDAgCkwgNTk0IDM1MDAgCkwgNTk0IDQ0OTQgCkwgMTE3MiA0NDk0IAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTc1IiBkPSJNIDU0NCAxMzgxIApMIDU0NCAzNTAwIApMIDExMTkgMzUwMCAKTCAxMTE5IDE0MDMgClEgMTExOSA5MDYgMTMxMiA2NTcgClEgMTUwNiA0MDkgMTg5NCA0MDkgClEgMjM1OSA0MDkgMjYyOSA3MDYgClEgMjkwMCAxMDAzIDI5MDAgMTUxNiAKTCAyOTAwIDM1MDAgCkwgMzQ3NSAzNTAwIApMIDM0NzUgMCAKTCAyOTAwIDAgCkwgMjkwMCA1MzggClEgMjY5MSAyMTkgMjQxNCA2NCAKUSAyMTM4IC05MSAxNzcyIC05MSAKUSAxMTY5IC05MSA4NTYgMjg0IApRIDU0NCA2NTkgNTQ0IDEzODEgCnoKTSAxOTkxIDM1ODQgCkwgMTk5MSAzNTg0IAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTcyIiBkPSJNIDI2MzEgMjk2MyAKUSAyNTM0IDMwMTkgMjQyMCAzMDQ1IApRIDIzMDYgMzA3MiAyMTY5IDMwNzIgClEgMTY4MSAzMDcyIDE0MjAgMjc1NSAKUSAxMTU5IDI0MzggMTE1OSAxODQ0IApMIDExNTkgMCAKTCA1ODEgMCAKTCA1ODEgMzUwMCAKTCAxMTU5IDM1MDAgCkwgMTE1OSAyOTU2IApRIDEzNDEgMzI3NSAxNjMxIDM0MjkgClEgMTkyMiAzNTg0IDIzMzggMzU4NCAKUSAyMzk3IDM1ODQgMjQ2OSAzNTc2IApRIDI1NDEgMzU2OSAyNjI4IDM1NTMgCkwgMjYzMSAyOTYzIAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTYyIiBkPSJNIDMxMTYgMTc0NyAKUSAzMTE2IDIzODEgMjg1NSAyNzQyIApRIDI1OTQgMzEwMyAyMTM4IDMxMDMgClEgMTY4MSAzMTAzIDE0MjAgMjc0MiAKUSAxMTU5IDIzODEgMTE1OSAxNzQ3IApRIDExNTkgMTExMyAxNDIwIDc1MiAKUSAxNjgxIDM5MSAyMTM4IDM5MSAKUSAyNTk0IDM5MSAyODU1IDc1MiAKUSAzMTE2IDExMTMgMzExNiAxNzQ3IAp6Ck0gMTE1OSAyOTY5IApRIDEzNDEgMzI4MSAxNjE3IDM0MzIgClEgMTg5NCAzNTg0IDIyNzggMzU4NCAKUSAyOTE2IDM1ODQgMzMxNCAzMDc4IApRIDM3MTMgMjU3MiAzNzEzIDE3NDcgClEgMzcxMyA5MjIgMzMxNCA0MTUgClEgMjkxNiAtOTEgMjI3OCAtOTEgClEgMTg5NCAtOTEgMTYxNyA2MSAKUSAxMzQxIDIxMyAxMTU5IDUyNSAKTCAxMTU5IDAgCkwgNTgxIDAgCkwgNTgxIDQ4NjMgCkwgMTE1OSA0ODYzIApMIDExNTkgMjk2OSAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8cGF0aCBpZD0iRGVqYVZ1U2Fucy02NSIgZD0iTSAzNTk3IDE4OTQgCkwgMzU5NyAxNjEzIApMIDk1MyAxNjEzIApRIDk5MSAxMDE5IDEzMTEgNzA4IApRIDE2MzEgMzk3IDIyMDMgMzk3IApRIDI1MzQgMzk3IDI4NDUgNDc4IApRIDMxNTYgNTU5IDM0NjMgNzIyIApMIDM0NjMgMTc4IApRIDMxNTMgNDcgMjgyOCAtMjIgClEgMjUwMyAtOTEgMjE2OSAtOTEgClEgMTMzMSAtOTEgODQyIDM5NiAKUSAzNTMgODg0IDM1MyAxNzE2IApRIDM1MyAyNTc1IDgxNyAzMDc5IApRIDEyODEgMzU4NCAyMDY5IDM1ODQgClEgMjc3NSAzNTg0IDMxODYgMzEyOSAKUSAzNTk3IDI2NzUgMzU5NyAxODk0IAp6Ck0gMzAyMiAyMDYzIApRIDMwMTYgMjUzNCAyNzU4IDI4MTUgClEgMjUwMCAzMDk3IDIwNzUgMzA5NyAKUSAxNTk0IDMwOTcgMTMwNSAyODI1IApRIDEwMTYgMjU1MyA5NzIgMjA1OSAKTCAzMDIyIDIwNjMgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtNzMiIGQ9Ik0gMjgzNCAzMzk3IApMIDI4MzQgMjg1MyAKUSAyNTkxIDI5NzggMjMyOCAzMDQwIApRIDIwNjYgMzEwMyAxNzg0IDMxMDMgClEgMTM1NiAzMTAzIDExNDIgMjk3MiAKUSA5MjggMjg0MSA5MjggMjU3OCAKUSA5MjggMjM3OCAxMDgxIDIyNjQgClEgMTIzNCAyMTUwIDE2OTcgMjA0NyAKTCAxODk0IDIwMDMgClEgMjUwNiAxODcyIDI3NjQgMTYzMyAKUSAzMDIyIDEzOTQgMzAyMiA5NjYgClEgMzAyMiA0NzggMjYzNiAxOTMgClEgMjI1MCAtOTEgMTU3NSAtOTEgClEgMTI5NCAtOTEgOTg5IC0zNiAKUSA2ODQgMTkgMzQ3IDEyOCAKTCAzNDcgNzIyIApRIDY2NiA1NTYgOTc1IDQ3MyAKUSAxMjg0IDM5MSAxNTg4IDM5MSAKUSAxOTk0IDM5MSAyMjEyIDUzMCAKUSAyNDMxIDY2OSAyNDMxIDkyMiAKUSAyNDMxIDExNTYgMjI3MyAxMjgxIApRIDIxMTYgMTQwNiAxNTgxIDE1MjIgCkwgMTM4MSAxNTY5IApRIDg0NyAxNjgxIDYwOSAxOTE0IApRIDM3MiAyMTQ3IDM3MiAyNTUzIApRIDM3MiAzMDQ3IDcyMiAzMzE1IApRIDEwNzIgMzU4NCAxNzE2IDM1ODQgClEgMjAzNCAzNTg0IDIzMTUgMzUzNyAKUSAyNTk3IDM0OTEgMjgzNCAzMzk3IAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgPC9kZWZzPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTRlIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNmYiIHg9Ijc0LjgwNDY4OCIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTJlIiB4PSIxMzQuMjM2MzI4Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMjAiIHg9IjE2Ni4wMjM0MzgiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03NyIgeD0iMTk3LjgxMDU0NyIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTY5IiB4PSIyNzkuNTk3NjU2Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNmUiIHg9IjMwNy4zODA4NTkiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy02NCIgeD0iMzcwLjc1OTc2NiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTIwIiB4PSI0MzQuMjM2MzI4Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNzQiIHg9IjQ2Ni4wMjM0MzgiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03NSIgeD0iNTA1LjIzMjQyMiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTcyIiB4PSI1NjguNjExMzI4Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNjIiIHg9IjYwOS43MjQ2MDkiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy02OSIgeD0iNjczLjIwMTE3MiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTZlIiB4PSI3MDAuOTg0Mzc1Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNjUiIHg9Ijc2NC4zNjMyODEiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03MyIgeD0iODI1Ljg4NjcxOSIvPgogICAgIDwvZz4KICAgIDwvZz4KICAgPC9nPgogICA8ZyBpZD0ibWF0cGxvdGxpYi5heGlzXzIiPgogICAgPGcgaWQ9Inl0aWNrXzEiPgogICAgIDxnIGlkPSJsaW5lMmRfMTkiPgogICAgICA8cGF0aCBkPSJNIDEwOCAyNDQuNDkwNDI5IApMIDQxMi4zNjM2MzYgMjQ0LjQ5MDQyOSAKIiBjbGlwLXBhdGg9InVybCgjcDA2M2M4ZjVlYjgpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzIwIj4KICAgICAgPGRlZnM+CiAgICAgICA8cGF0aCBpZD0ibTY3OGNmNTIyODIiIGQ9Ik0gMCAwIApMIC0zLjUgMCAKIiBzdHlsZT0ic3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuOCIvPgogICAgICA8L2RlZnM+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTY3OGNmNTIyODIiIHg9IjEwOCIgeT0iMjQ0LjQ5MDQyOSIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8xMSI+CiAgICAgIDwhLS0gMCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoOTQuNjM3NSAyNDguMjg5NjQ3KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIi8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieXRpY2tfMiI+CiAgICAgPGcgaWQ9ImxpbmUyZF8yMSI+CiAgICAgIDxwYXRoIGQ9Ik0gMTA4IDIxNS45NzE2NzggCkwgNDEyLjM2MzYzNiAyMTUuOTcxNjc4IAoiIGNsaXAtcGF0aD0idXJsKCNwMDYzYzhmNWViOCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfMjIiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI202NzhjZjUyMjgyIiB4PSIxMDgiIHk9IjIxNS45NzE2NzgiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMTIiPgogICAgICA8IS0tIDUwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg4OC4yNzUgMjE5Ljc3MDg5NilzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zNSIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieXRpY2tfMyI+CiAgICAgPGcgaWQ9ImxpbmUyZF8yMyI+CiAgICAgIDxwYXRoIGQ9Ik0gMTA4IDE4Ny40NTI5MjcgCkwgNDEyLjM2MzYzNiAxODcuNDUyOTI3IAoiIGNsaXAtcGF0aD0idXJsKCNwMDYzYzhmNWViOCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfMjQiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI202NzhjZjUyMjgyIiB4PSIxMDgiIHk9IjE4Ny40NTI5MjciIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMTMiPgogICAgICA8IS0tIDEwMCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoODEuOTEyNSAxOTEuMjUyMTQ2KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMxIi8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ5dGlja180Ij4KICAgICA8ZyBpZD0ibGluZTJkXzI1Ij4KICAgICAgPHBhdGggZD0iTSAxMDggMTU4LjkzNDE3NiAKTCA0MTIuMzYzNjM2IDE1OC45MzQxNzYgCiIgY2xpcC1wYXRoPSJ1cmwoI3AwNjNjOGY1ZWI4KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2IwYjBiMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgICA8L2c+CiAgICAgPGcgaWQ9ImxpbmUyZF8yNiI+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTY3OGNmNTIyODIiIHg9IjEwOCIgeT0iMTU4LjkzNDE3NiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8xNCI+CiAgICAgIDwhLS0gMTUwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg4MS45MTI1IDE2Mi43MzMzOTUpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzEiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzUiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9Inl0aWNrXzUiPgogICAgIDxnIGlkPSJsaW5lMmRfMjciPgogICAgICA8cGF0aCBkPSJNIDEwOCAxMzAuNDE1NDI1IApMIDQxMi4zNjM2MzYgMTMwLjQxNTQyNSAKIiBjbGlwLXBhdGg9InVybCgjcDA2M2M4ZjVlYjgpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzI4Ij4KICAgICAgPGc+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNtNjc4Y2Y1MjI4MiIgeD0iMTA4IiB5PSIxMzAuNDE1NDI1IiBzdHlsZT0ic3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuOCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgIDxnIGlkPSJ0ZXh0XzE1Ij4KICAgICAgPCEtLSAyMDAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDgxLjkxMjUgMTM0LjIxNDY0NClzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMiIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSIxMjcuMjQ2MDk0Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieXRpY2tfNiI+CiAgICAgPGcgaWQ9ImxpbmUyZF8yOSI+CiAgICAgIDxwYXRoIGQ9Ik0gMTA4IDEwMS44OTY2NzQgCkwgNDEyLjM2MzYzNiAxMDEuODk2Njc0IAoiIGNsaXAtcGF0aD0idXJsKCNwMDYzYzhmNWViOCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfMzAiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI202NzhjZjUyMjgyIiB4PSIxMDgiIHk9IjEwMS44OTY2NzQiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMTYiPgogICAgICA8IS0tIDI1MCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoODEuOTEyNSAxMDUuNjk1ODkzKXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMyIi8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM1IiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ5dGlja183Ij4KICAgICA8ZyBpZD0ibGluZTJkXzMxIj4KICAgICAgPHBhdGggZD0iTSAxMDggNzMuMzc3OTI0IApMIDQxMi4zNjM2MzYgNzMuMzc3OTI0IAoiIGNsaXAtcGF0aD0idXJsKCNwMDYzYzhmNWViOCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfMzIiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI202NzhjZjUyMjgyIiB4PSIxMDgiIHk9IjczLjM3NzkyNCIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8xNyI+CiAgICAgIDwhLS0gMzAwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg4MS45MTI1IDc3LjE3NzE0MilzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSIxMjcuMjQ2MDk0Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieXRpY2tfOCI+CiAgICAgPGcgaWQ9ImxpbmUyZF8zMyI+CiAgICAgIDxwYXRoIGQ9Ik0gMTA4IDQ0Ljg1OTE3MyAKTCA0MTIuMzYzNjM2IDQ0Ljg1OTE3MyAKIiBjbGlwLXBhdGg9InVybCgjcDA2M2M4ZjVlYjgpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzM0Ij4KICAgICAgPGc+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNtNjc4Y2Y1MjI4MiIgeD0iMTA4IiB5PSI0NC44NTkxNzMiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMTgiPgogICAgICA8IS0tIDM1MCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoODEuOTEyNSA0OC42NTgzOTIpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzMiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzUiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9InRleHRfMTkiPgogICAgIDwhLS0gVGltZSBbc10gLS0+CiAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoNzUuODMyODEyIDE2My42MDg5MDYpcm90YXRlKC05MClzY2FsZSgwLjEgLTAuMSkiPgogICAgICA8ZGVmcz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTU0IiBkPSJNIC0xOSA0NjY2IApMIDM5MjggNDY2NiAKTCAzOTI4IDQxMzQgCkwgMjI3MiA0MTM0IApMIDIyNzIgMCAKTCAxNjM4IDAgCkwgMTYzOCA0MTM0IApMIC0xOSA0MTM0IApMIC0xOSA0NjY2IAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTZkIiBkPSJNIDMzMjggMjgyOCAKUSAzNTQ0IDMyMTYgMzg0NCAzNDAwIApRIDQxNDQgMzU4NCA0NTUwIDM1ODQgClEgNTA5NyAzNTg0IDUzOTQgMzIwMSAKUSA1NjkxIDI4MTkgNTY5MSAyMTEzIApMIDU2OTEgMCAKTCA1MTEzIDAgCkwgNTExMyAyMDk0IApRIDUxMTMgMjU5NyA0OTM0IDI4NDAgClEgNDc1NiAzMDg0IDQzOTEgMzA4NCAKUSAzOTQ0IDMwODQgMzY4NCAyNzg3IApRIDM0MjUgMjQ5MSAzNDI1IDE5NzggCkwgMzQyNSAwIApMIDI4NDcgMCAKTCAyODQ3IDIwOTQgClEgMjg0NyAyNjAwIDI2NjkgMjg0MiAKUSAyNDkxIDMwODQgMjExOSAzMDg0IApRIDE2NzggMzA4NCAxNDE4IDI3ODYgClEgMTE1OSAyNDg4IDExNTkgMTk3OCAKTCAxMTU5IDAgCkwgNTgxIDAgCkwgNTgxIDM1MDAgCkwgMTE1OSAzNTAwIApMIDExNTkgMjk1NiAKUSAxMzU2IDMyNzggMTYzMSAzNDMxIApRIDE5MDYgMzU4NCAyMjg0IDM1ODQgClEgMjY2NiAzNTg0IDI5MzMgMzM5MCAKUSAzMjAwIDMxOTcgMzMyOCAyODI4IAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTViIiBkPSJNIDU1MCA0ODYzIApMIDE4NzUgNDg2MyAKTCAxODc1IDQ0MTYgCkwgMTEyNSA0NDE2IApMIDExMjUgLTM5NyAKTCAxODc1IC0zOTcgCkwgMTg3NSAtODQ0IApMIDU1MCAtODQ0IApMIDU1MCA0ODYzIAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTVkIiBkPSJNIDE5NDcgNDg2MyAKTCAxOTQ3IC04NDQgCkwgNjIyIC04NDQgCkwgNjIyIC0zOTcgCkwgMTM2OSAtMzk3IApMIDEzNjkgNDQxNiAKTCA2MjIgNDQxNiAKTCA2MjIgNDg2MyAKTCAxOTQ3IDQ4NjMgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICA8L2RlZnM+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNTQiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy02OSIgeD0iNTcuOTU4OTg0Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNmQiIHg9Ijg1Ljc0MjE4OCIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTY1IiB4PSIxODMuMTU0Mjk3Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMjAiIHg9IjI0NC42Nzc3MzQiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy01YiIgeD0iMjc2LjQ2NDg0NCIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTczIiB4PSIzMTUuNDc4NTE2Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNWQiIHg9IjM2Ny41NzgxMjUiLz4KICAgICA8L2c+CiAgICA8L2c+CiAgIDwvZz4KICAgPGcgaWQ9ImxpbmUyZF8zNSI+CiAgICA8cGF0aCBkPSJNIDEyMS44MzQ3MTEgMjM2LjQ3NjU3NCAKTCAxOTEuMDA4MjY0IDIxMy45NjYyMjIgCkwgMjYwLjE4MTgxOCAxNzIuNDMxNTg5IApMIDMyOS4zNTUzNzIgMTE2LjA4MDIyOCAKTCAzOTguNTI4OTI2IDQ0LjQ0MzYzNiAKIiBjbGlwLXBhdGg9InVybCgjcDA2M2M4ZjVlYjgpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjMWY3N2I0OyBzdHJva2Utd2lkdGg6IDEuNTsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICA8L2c+CiAgIDxnIGlkPSJsaW5lMmRfMzYiPgogICAgPHBhdGggZD0iTSAxMjEuODM0NzExIDI0MS42MTA3MTQgCkwgMTkxLjAwODI2NCAyMzUuMzkzNDE4IApMIDI2MC4xODE4MTggMjIzLjk1MzU4MiAKTCAzMjkuMzU1MzcyIDIwOS4xMTM2MTcgCkwgMzk4LjUyODkyNiAxODkuNjE4NTM2IAoiIGNsaXAtcGF0aD0idXJsKCNwMDYzYzhmNWViOCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNmZjdmMGU7IHN0cm9rZS13aWR0aDogMS41OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgIDwvZz4KICAgPGcgaWQ9ImxpbmUyZF8zNyI+CiAgICA8cGF0aCBkPSJNIDEyMS44MzQ3MTEgMjQyLjExNjM2NCAKTCAxOTEuMDA4MjY0IDI0MC45NTMzMjcgCkwgMjYwLjE4MTgxOCAyMzYuNDk3MDU4IApMIDMyOS4zNTUzNzIgMjMwLjc3Mjg0MyAKTCAzOTguNTI4OTI2IDIyNC4yNzk4MTkgCiIgY2xpcC1wYXRoPSJ1cmwoI3AwNjNjOGY1ZWI4KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogIzJjYTAyYzsgc3Ryb2tlLXdpZHRoOiAxLjU7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgPC9nPgogICA8ZyBpZD0ibGluZTJkXzM4Ij4KICAgIDxwYXRoIGQ9Ik0gMTIxLjgzNDcxMSAyNDAuOTg1NTAxIApMIDE5MS4wMDgyNjQgMjQxLjYzNjc1MiAKTCAyNjAuMTgxODE4IDIzNy45MDMwODIgCkwgMzI5LjM1NTM3MiAyMzMuMDU4MTM1IApMIDM5OC41Mjg5MjYgMjI4LjY5NDY4MiAKIiBjbGlwLXBhdGg9InVybCgjcDA2M2M4ZjVlYjgpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjZDYyNzI4OyBzdHJva2Utd2lkdGg6IDEuNTsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICA8L2c+CiAgIDxnIGlkPSJwYXRjaF8zIj4KICAgIDxwYXRoIGQ9Ik0gMTA4IDI1MiAKTCAxMDggMzQuNTYgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lam9pbjogbWl0ZXI7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgPC9nPgogICA8ZyBpZD0icGF0Y2hfNCI+CiAgICA8cGF0aCBkPSJNIDQxMi4zNjM2MzYgMjUyIApMIDQxMi4zNjM2MzYgMzQuNTYgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lam9pbjogbWl0ZXI7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgPC9nPgogICA8ZyBpZD0icGF0Y2hfNSI+CiAgICA8cGF0aCBkPSJNIDEwOCAyNTIgCkwgNDEyLjM2MzYzNiAyNTIgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lam9pbjogbWl0ZXI7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgPC9nPgogICA8ZyBpZD0icGF0Y2hfNiI+CiAgICA8cGF0aCBkPSJNIDEwOCAzNC41NiAKTCA0MTIuMzYzNjM2IDM0LjU2IAoiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWpvaW46IG1pdGVyOyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgIDwvZz4KICAgPGcgaWQ9ImxlZ2VuZF8xIj4KICAgIDxnIGlkPSJwYXRjaF83Ij4KICAgICA8cGF0aCBkPSJNIDExNSAxMDEuMjcyNSAKTCAxODguNDQzNzUgMTAxLjI3MjUgClEgMTkwLjQ0Mzc1IDEwMS4yNzI1IDE5MC40NDM3NSA5OS4yNzI1IApMIDE5MC40NDM3NSA0MS41NiAKUSAxOTAuNDQzNzUgMzkuNTYgMTg4LjQ0Mzc1IDM5LjU2IApMIDExNSAzOS41NiAKUSAxMTMgMzkuNTYgMTEzIDQxLjU2IApMIDExMyA5OS4yNzI1IApRIDExMyAxMDEuMjcyNSAxMTUgMTAxLjI3MjUgCnoKIiBzdHlsZT0iZmlsbDogI2ZmZmZmZjsgb3BhY2l0eTogMC44OyBzdHJva2U6ICNjY2NjY2M7IHN0cm9rZS1saW5lam9pbjogbWl0ZXIiLz4KICAgIDwvZz4KICAgIDxnIGlkPSJsaW5lMmRfMzkiPgogICAgIDxwYXRoIGQ9Ik0gMTE3IDQ3LjY1ODQzNyAKTCAxMjcgNDcuNjU4NDM3IApMIDEzNyA0Ny42NTg0MzcgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogIzFmNzdiNDsgc3Ryb2tlLXdpZHRoOiAxLjU7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgIDwvZz4KICAgIDxnIGlkPSJ0ZXh0XzIwIj4KICAgICA8IS0tIDEgQ1BVcyAtLT4KICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSgxNDUgNTEuMTU4NDM3KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgIDxkZWZzPgogICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtNDMiIGQ9Ik0gNDEyMiA0MzA2IApMIDQxMjIgMzY0MSAKUSAzODAzIDM5MzggMzQ0MiA0MDg0IApRIDMwODEgNDIzMSAyNjc1IDQyMzEgClEgMTg3NSA0MjMxIDE0NTAgMzc0MiAKUSAxMDI1IDMyNTMgMTAyNSAyMzI4IApRIDEwMjUgMTQwNiAxNDUwIDkxNyAKUSAxODc1IDQyOCAyNjc1IDQyOCAKUSAzMDgxIDQyOCAzNDQyIDU3NSAKUSAzODAzIDcyMiA0MTIyIDEwMTkgCkwgNDEyMiAzNTkgClEgMzc5MSAxMzQgMzQyMCAyMSAKUSAzMDUwIC05MSAyNjM4IC05MSAKUSAxNTc4IC05MSA5NjggNTU3IApRIDM1OSAxMjA2IDM1OSAyMzI4IApRIDM1OSAzNDUzIDk2OCA0MTAxIApRIDE1NzggNDc1MCAyNjM4IDQ3NTAgClEgMzA1NiA0NzUwIDM0MjYgNDYzOSAKUSAzNzk3IDQ1MjggNDEyMiA0MzA2IAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTUwIiBkPSJNIDEyNTkgNDE0NyAKTCAxMjU5IDIzOTQgCkwgMjA1MyAyMzk0IApRIDI0OTQgMjM5NCAyNzM0IDI2MjIgClEgMjk3NSAyODUwIDI5NzUgMzI3MiAKUSAyOTc1IDM2OTEgMjczNCAzOTE5IApRIDI0OTQgNDE0NyAyMDUzIDQxNDcgCkwgMTI1OSA0MTQ3IAp6Ck0gNjI4IDQ2NjYgCkwgMjA1MyA0NjY2IApRIDI4MzggNDY2NiAzMjM5IDQzMTEgClEgMzY0MSAzOTU2IDM2NDEgMzI3MiAKUSAzNjQxIDI1ODEgMzIzOSAyMjI4IApRIDI4MzggMTg3NSAyMDUzIDE4NzUgCkwgMTI1OSAxODc1IApMIDEyNTkgMCAKTCA2MjggMCAKTCA2MjggNDY2NiAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8cGF0aCBpZD0iRGVqYVZ1U2Fucy01NSIgZD0iTSA1NTYgNDY2NiAKTCAxMTkxIDQ2NjYgCkwgMTE5MSAxODMxIApRIDExOTEgMTA4MSAxNDYyIDc1MSAKUSAxNzM0IDQyMiAyMzQ0IDQyMiAKUSAyOTUwIDQyMiAzMjIyIDc1MSAKUSAzNDk0IDEwODEgMzQ5NCAxODMxIApMIDM0OTQgNDY2NiAKTCA0MTI4IDQ2NjYgCkwgNDEyOCAxNzUzIApRIDQxMjggODQxIDM2NzYgMzc1IApRIDMyMjUgLTkxIDIzNDQgLTkxIApRIDE0NTkgLTkxIDEwMDcgMzc1IApRIDU1NiA4NDEgNTU2IDE3NTMgCkwgNTU2IDQ2NjYgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICA8L2RlZnM+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzEiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0yMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNDMiIHg9Ijk1LjQxMDE1NiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTUwIiB4PSIxNjUuMjM0Mzc1Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNTUiIHg9IjIyNS41MzcxMDkiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03MyIgeD0iMjk4LjczMDQ2OSIvPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJsaW5lMmRfNDAiPgogICAgIDxwYXRoIGQ9Ik0gMTE3IDYyLjMzNjU2MiAKTCAxMjcgNjIuMzM2NTYyIApMIDEzNyA2Mi4zMzY1NjIgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2ZmN2YwZTsgc3Ryb2tlLXdpZHRoOiAxLjU7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgIDwvZz4KICAgIDxnIGlkPSJ0ZXh0XzIxIj4KICAgICA8IS0tIDQgQ1BVcyAtLT4KICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSgxNDUgNjUuODM2NTYyKXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzQiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0yMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNDMiIHg9Ijk1LjQxMDE1NiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTUwIiB4PSIxNjUuMjM0Mzc1Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNTUiIHg9IjIyNS41MzcxMDkiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03MyIgeD0iMjk4LjczMDQ2OSIvPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJsaW5lMmRfNDEiPgogICAgIDxwYXRoIGQ9Ik0gMTE3IDc3LjAxNDY4NyAKTCAxMjcgNzcuMDE0Njg3IApMIDEzNyA3Ny4wMTQ2ODcgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogIzJjYTAyYzsgc3Ryb2tlLXdpZHRoOiAxLjU7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgIDwvZz4KICAgIDxnIGlkPSJ0ZXh0XzIyIj4KICAgICA8IS0tIDE2IENQVXMgLS0+CiAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoMTQ1IDgwLjUxNDY4NylzY2FsZSgwLjEgLTAuMSkiPgogICAgICA8ZGVmcz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTM2IiBkPSJNIDIxMTMgMjU4NCAKUSAxNjg4IDI1ODQgMTQzOSAyMjkzIApRIDExOTEgMjAwMyAxMTkxIDE0OTcgClEgMTE5MSA5OTQgMTQzOSA3MDEgClEgMTY4OCA0MDkgMjExMyA0MDkgClEgMjUzOCA0MDkgMjc4NiA3MDEgClEgMzAzNCA5OTQgMzAzNCAxNDk3IApRIDMwMzQgMjAwMyAyNzg2IDIyOTMgClEgMjUzOCAyNTg0IDIxMTMgMjU4NCAKegpNIDMzNjYgNDU2MyAKTCAzMzY2IDM5ODggClEgMzEyOCA0MTAwIDI4ODYgNDE1OSAKUSAyNjQ0IDQyMTkgMjQwNiA0MjE5IApRIDE3ODEgNDIxOSAxNDUxIDM3OTcgClEgMTEyMiAzMzc1IDEwNzUgMjUyMiAKUSAxMjU5IDI3OTQgMTUzNyAyOTM5IApRIDE4MTYgMzA4NCAyMTUwIDMwODQgClEgMjg1MyAzMDg0IDMyNjEgMjY1NyAKUSAzNjY5IDIyMzEgMzY2OSAxNDk3IApRIDM2NjkgNzc4IDMyNDQgMzQzIApRIDI4MTkgLTkxIDIxMTMgLTkxIApRIDEzMDMgLTkxIDg3NSA1MjkgClEgNDQ3IDExNTAgNDQ3IDIzMjggClEgNDQ3IDM0MzQgOTcyIDQwOTIgClEgMTQ5NyA0NzUwIDIzODEgNDc1MCAKUSAyNjE5IDQ3NTAgMjg2MSA0NzAzIApRIDMxMDMgNDY1NiAzMzY2IDQ1NjMgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICA8L2RlZnM+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzEiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zNiIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMjAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy00MyIgeD0iMTU5LjAzMzIwMyIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTUwIiB4PSIyMjguODU3NDIyIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNTUiIHg9IjI4OS4xNjAxNTYiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03MyIgeD0iMzYyLjM1MzUxNiIvPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJsaW5lMmRfNDIiPgogICAgIDxwYXRoIGQ9Ik0gMTE3IDkxLjY5MjgxMyAKTCAxMjcgOTEuNjkyODEzIApMIDEzNyA5MS42OTI4MTMgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2Q2MjcyODsgc3Ryb2tlLXdpZHRoOiAxLjU7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgIDwvZz4KICAgIDxnIGlkPSJ0ZXh0XzIzIj4KICAgICA8IS0tIDMyIENQVXMgLS0+CiAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoMTQ1IDk1LjE5MjgxMylzY2FsZSgwLjEgLTAuMSkiPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMzIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzIiIHg9IjYzLjYyMzA0NyIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTIwIiB4PSIxMjcuMjQ2MDk0Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNDMiIHg9IjE1OS4wMzMyMDMiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy01MCIgeD0iMjI4Ljg1NzQyMiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTU1IiB4PSIyODkuMTYwMTU2Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNzMiIHg9IjM2Mi4zNTM1MTYiLz4KICAgICA8L2c+CiAgICA8L2c+CiAgIDwvZz4KICA8L2c+CiAgPGcgaWQ9ImF4ZXNfMiI+CiAgIDxnIGlkPSJwYXRjaF84Ij4KICAgIDxwYXRoIGQ9Ik0gNDczLjIzNjM2NCAyNTIgCkwgNzc3LjYgMjUyIApMIDc3Ny42IDM0LjU2IApMIDQ3My4yMzYzNjQgMzQuNTYgCnoKIiBzdHlsZT0iZmlsbDogI2ZmZmZmZiIvPgogICA8L2c+CiAgIDxnIGlkPSJtYXRwbG90bGliLmF4aXNfMyI+CiAgICA8ZyBpZD0ieHRpY2tfMTAiPgogICAgIDxnIGlkPSJsaW5lMmRfNDMiPgogICAgICA8cGF0aCBkPSJNIDQ4Ny4wNzEwNzQgMjUyIApMIDQ4Ny4wNzEwNzQgMzQuNTYgCiIgY2xpcC1wYXRoPSJ1cmwoI3AyOGE0YjY1YzM0KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2IwYjBiMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgICA8L2c+CiAgICAgPGcgaWQ9ImxpbmUyZF80NCI+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTU4M2I2ZTVmNTkiIHg9IjQ4Ny4wNzEwNzQiIHk9IjI1MiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8yNCI+CiAgICAgIDwhLS0gMTAwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg0NzcuNTI3MzI0IDI2Ni41OTg0Mzcpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzEiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9Inh0aWNrXzExIj4KICAgICA8ZyBpZD0ibGluZTJkXzQ1Ij4KICAgICAgPHBhdGggZD0iTSA1MjEuNjU3ODUxIDI1MiAKTCA1MjEuNjU3ODUxIDM0LjU2IAoiIGNsaXAtcGF0aD0idXJsKCNwMjhhNGI2NWMzNCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfNDYiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI201ODNiNmU1ZjU5IiB4PSI1MjEuNjU3ODUxIiB5PSIyNTIiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMjUiPgogICAgICA8IS0tIDE1MCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoNTEyLjExNDEwMSAyNjYuNTk4NDM3KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMxIi8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM1IiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ4dGlja18xMiI+CiAgICAgPGcgaWQ9ImxpbmUyZF80NyI+CiAgICAgIDxwYXRoIGQ9Ik0gNTU2LjI0NDYyOCAyNTIgCkwgNTU2LjI0NDYyOCAzNC41NiAKIiBjbGlwLXBhdGg9InVybCgjcDI4YTRiNjVjMzQpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzQ4Ij4KICAgICAgPGc+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNtNTgzYjZlNWY1OSIgeD0iNTU2LjI0NDYyOCIgeT0iMjUyIiBzdHlsZT0ic3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuOCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgIDxnIGlkPSJ0ZXh0XzI2Ij4KICAgICAgPCEtLSAyMDAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDU0Ni43MDA4NzggMjY2LjU5ODQzNylzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMiIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSIxMjcuMjQ2MDk0Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieHRpY2tfMTMiPgogICAgIDxnIGlkPSJsaW5lMmRfNDkiPgogICAgICA8cGF0aCBkPSJNIDU5MC44MzE0MDUgMjUyIApMIDU5MC44MzE0MDUgMzQuNTYgCiIgY2xpcC1wYXRoPSJ1cmwoI3AyOGE0YjY1YzM0KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2IwYjBiMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgICA8L2c+CiAgICAgPGcgaWQ9ImxpbmUyZF81MCI+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTU4M2I2ZTVmNTkiIHg9IjU5MC44MzE0MDUiIHk9IjI1MiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8yNyI+CiAgICAgIDwhLS0gMjUwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg1ODEuMjg3NjU1IDI2Ni41OTg0Mzcpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzIiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzUiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9Inh0aWNrXzE0Ij4KICAgICA8ZyBpZD0ibGluZTJkXzUxIj4KICAgICAgPHBhdGggZD0iTSA2MjUuNDE4MTgyIDI1MiAKTCA2MjUuNDE4MTgyIDM0LjU2IAoiIGNsaXAtcGF0aD0idXJsKCNwMjhhNGI2NWMzNCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfNTIiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI201ODNiNmU1ZjU5IiB4PSI2MjUuNDE4MTgyIiB5PSIyNTIiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMjgiPgogICAgICA8IS0tIDMwMCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoNjE1Ljg3NDQzMiAyNjYuNTk4NDM3KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMzIi8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ4dGlja18xNSI+CiAgICAgPGcgaWQ9ImxpbmUyZF81MyI+CiAgICAgIDxwYXRoIGQ9Ik0gNjYwLjAwNDk1OSAyNTIgCkwgNjYwLjAwNDk1OSAzNC41NiAKIiBjbGlwLXBhdGg9InVybCgjcDI4YTRiNjVjMzQpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzU0Ij4KICAgICAgPGc+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNtNTgzYjZlNWY1OSIgeD0iNjYwLjAwNDk1OSIgeT0iMjUyIiBzdHlsZT0ic3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuOCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgIDxnIGlkPSJ0ZXh0XzI5Ij4KICAgICAgPCEtLSAzNTAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDY1MC40NjEyMDkgMjY2LjU5ODQzNylzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zNSIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSIxMjcuMjQ2MDk0Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieHRpY2tfMTYiPgogICAgIDxnIGlkPSJsaW5lMmRfNTUiPgogICAgICA8cGF0aCBkPSJNIDY5NC41OTE3MzYgMjUyIApMIDY5NC41OTE3MzYgMzQuNTYgCiIgY2xpcC1wYXRoPSJ1cmwoI3AyOGE0YjY1YzM0KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2IwYjBiMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgICA8L2c+CiAgICAgPGcgaWQ9ImxpbmUyZF81NiI+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTU4M2I2ZTVmNTkiIHg9IjY5NC41OTE3MzYiIHk9IjI1MiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8zMCI+CiAgICAgIDwhLS0gNDAwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg2ODUuMDQ3OTg2IDI2Ni41OTg0Mzcpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzQiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9Inh0aWNrXzE3Ij4KICAgICA8ZyBpZD0ibGluZTJkXzU3Ij4KICAgICAgPHBhdGggZD0iTSA3MjkuMTc4NTEyIDI1MiAKTCA3MjkuMTc4NTEyIDM0LjU2IAoiIGNsaXAtcGF0aD0idXJsKCNwMjhhNGI2NWMzNCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfNTgiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI201ODNiNmU1ZjU5IiB4PSI3MjkuMTc4NTEyIiB5PSIyNTIiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMzEiPgogICAgICA8IS0tIDQ1MCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoNzE5LjYzNDc2MiAyNjYuNTk4NDM3KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM0Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM1IiB4PSI2My42MjMwNDciLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ4dGlja18xOCI+CiAgICAgPGcgaWQ9ImxpbmUyZF81OSI+CiAgICAgIDxwYXRoIGQ9Ik0gNzYzLjc2NTI4OSAyNTIgCkwgNzYzLjc2NTI4OSAzNC41NiAKIiBjbGlwLXBhdGg9InVybCgjcDI4YTRiNjVjMzQpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzYwIj4KICAgICAgPGc+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNtNTgzYjZlNWY1OSIgeD0iNzYzLjc2NTI4OSIgeT0iMjUyIiBzdHlsZT0ic3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuOCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgIDxnIGlkPSJ0ZXh0XzMyIj4KICAgICAgPCEtLSA1MDAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDc1NC4yMjE1MzkgMjY2LjU5ODQzNylzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zNSIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSIxMjcuMjQ2MDk0Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0idGV4dF8zMyI+CiAgICAgPCEtLSBOby4gd2luZCB0dXJiaW5lcyAtLT4KICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg1ODEuNTE5NzQ0IDI4MC4yNzY1NjMpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy00ZSIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTZmIiB4PSI3NC44MDQ2ODgiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0yZSIgeD0iMTM0LjIzNjMyOCIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTIwIiB4PSIxNjYuMDIzNDM4Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNzciIHg9IjE5Ny44MTA1NDciLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy02OSIgeD0iMjc5LjU5NzY1NiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTZlIiB4PSIzMDcuMzgwODU5Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNjQiIHg9IjM3MC43NTk3NjYiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0yMCIgeD0iNDM0LjIzNjMyOCIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTc0IiB4PSI0NjYuMDIzNDM4Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNzUiIHg9IjUwNS4yMzI0MjIiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03MiIgeD0iNTY4LjYxMTMyOCIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTYyIiB4PSI2MDkuNzI0NjA5Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNjkiIHg9IjY3My4yMDExNzIiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy02ZSIgeD0iNzAwLjk4NDM3NSIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTY1IiB4PSI3NjQuMzYzMjgxIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNzMiIHg9IjgyNS44ODY3MTkiLz4KICAgICA8L2c+CiAgICA8L2c+CiAgIDwvZz4KICAgPGcgaWQ9Im1hdHBsb3RsaWIuYXhpc180Ij4KICAgIDxnIGlkPSJ5dGlja185Ij4KICAgICA8ZyBpZD0ibGluZTJkXzYxIj4KICAgICAgPHBhdGggZD0iTSA0NzMuMjM2MzY0IDIxNC43NTA1MzIgCkwgNzc3LjYgMjE0Ljc1MDUzMiAKIiBjbGlwLXBhdGg9InVybCgjcDI4YTRiNjVjMzQpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjYjBiMGIwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgIDwvZz4KICAgICA8ZyBpZD0ibGluZTJkXzYyIj4KICAgICAgPGc+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNtNjc4Y2Y1MjI4MiIgeD0iNDczLjIzNjM2NCIgeT0iMjE0Ljc1MDUzMiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8zNCI+CiAgICAgIDwhLS0gMjAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDQ1My41MTEzNjQgMjE4LjU0OTc1MSlzY2FsZSgwLjEgLTAuMSkiPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMiIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ieXRpY2tfMTAiPgogICAgIDxnIGlkPSJsaW5lMmRfNjMiPgogICAgICA8cGF0aCBkPSJNIDQ3My4yMzYzNjQgMTcyLjE3MzgwOCAKTCA3NzcuNiAxNzIuMTczODA4IAoiIGNsaXAtcGF0aD0idXJsKCNwMjhhNGI2NWMzNCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfNjQiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI202NzhjZjUyMjgyIiB4PSI0NzMuMjM2MzY0IiB5PSIxNzIuMTczODA4IiBzdHlsZT0ic3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuOCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgIDxnIGlkPSJ0ZXh0XzM1Ij4KICAgICAgPCEtLSA0MCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoNDUzLjUxMTM2NCAxNzUuOTczMDI3KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM0Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSI2My42MjMwNDciLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ5dGlja18xMSI+CiAgICAgPGcgaWQ9ImxpbmUyZF82NSI+CiAgICAgIDxwYXRoIGQ9Ik0gNDczLjIzNjM2NCAxMjkuNTk3MDg0IApMIDc3Ny42IDEyOS41OTcwODQgCiIgY2xpcC1wYXRoPSJ1cmwoI3AyOGE0YjY1YzM0KSIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2IwYjBiMDsgc3Ryb2tlLXdpZHRoOiAwLjg7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgICA8L2c+CiAgICAgPGcgaWQ9ImxpbmUyZF82NiI+CiAgICAgIDxnPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjbTY3OGNmNTIyODIiIHg9IjQ3My4yMzYzNjQiIHk9IjEyOS41OTcwODQiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMzYiPgogICAgICA8IS0tIDYwIC0tPgogICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg0NTMuNTExMzY0IDEzMy4zOTYzMDMpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzYiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjYzLjYyMzA0NyIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9Inl0aWNrXzEyIj4KICAgICA8ZyBpZD0ibGluZTJkXzY3Ij4KICAgICAgPHBhdGggZD0iTSA0NzMuMjM2MzY0IDg3LjAyMDM2IApMIDc3Ny42IDg3LjAyMDM2IAoiIGNsaXAtcGF0aD0idXJsKCNwMjhhNGI2NWMzNCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfNjgiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI202NzhjZjUyMjgyIiB4PSI0NzMuMjM2MzY0IiB5PSI4Ny4wMjAzNiIgc3R5bGU9InN0cm9rZTogIzAwMDAwMDsgc3Ryb2tlLXdpZHRoOiAwLjgiLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgICA8ZyBpZD0idGV4dF8zNyI+CiAgICAgIDwhLS0gODAgLS0+CiAgICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDQ1My41MTEzNjQgOTAuODE5NTc5KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgICA8ZGVmcz4KICAgICAgICA8cGF0aCBpZD0iRGVqYVZ1U2Fucy0zOCIgZD0iTSAyMDM0IDIyMTYgClEgMTU4NCAyMjE2IDEzMjYgMTk3NSAKUSAxMDY5IDE3MzQgMTA2OSAxMzEzIApRIDEwNjkgODkxIDEzMjYgNjUwIApRIDE1ODQgNDA5IDIwMzQgNDA5IApRIDI0ODQgNDA5IDI3NDMgNjUxIApRIDMwMDMgODk0IDMwMDMgMTMxMyAKUSAzMDAzIDE3MzQgMjc0NSAxOTc1IApRIDI0ODggMjIxNiAyMDM0IDIyMTYgCnoKTSAxNDAzIDI0ODQgClEgOTk3IDI1ODQgNzcwIDI4NjIgClEgNTQ0IDMxNDEgNTQ0IDM1NDEgClEgNTQ0IDQxMDAgOTQyIDQ0MjUgClEgMTM0MSA0NzUwIDIwMzQgNDc1MCAKUSAyNzMxIDQ3NTAgMzEyOCA0NDI1IApRIDM1MjUgNDEwMCAzNTI1IDM1NDEgClEgMzUyNSAzMTQxIDMyOTggMjg2MiAKUSAzMDcyIDI1ODQgMjY2OSAyNDg0IApRIDMxMjUgMjM3OCAzMzc5IDIwNjggClEgMzYzNCAxNzU5IDM2MzQgMTMxMyAKUSAzNjM0IDYzNCAzMjIwIDI3MSAKUSAyODA2IC05MSAyMDM0IC05MSAKUSAxMjYzIC05MSA4NDggMjcxIApRIDQzNCA2MzQgNDM0IDEzMTMgClEgNDM0IDE3NTkgNjkwIDIwNjggClEgOTQ3IDIzNzggMTQwMyAyNDg0IAp6Ck0gMTE3MiAzNDgxIApRIDExNzIgMzExOSAxMzk4IDI5MTYgClEgMTYyNSAyNzEzIDIwMzQgMjcxMyAKUSAyNDQxIDI3MTMgMjY3MCAyOTE2IApRIDI5MDAgMzExOSAyOTAwIDM0ODEgClEgMjkwMCAzODQ0IDI2NzAgNDA0NyAKUSAyNDQxIDQyNTAgMjAzNCA0MjUwIApRIDE2MjUgNDI1MCAxMzk4IDQwNDcgClEgMTE3MiAzODQ0IDExNzIgMzQ4MSAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8L2RlZnM+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM4Ii8+CiAgICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMwIiB4PSI2My42MjMwNDciLz4KICAgICAgPC9nPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJ5dGlja18xMyI+CiAgICAgPGcgaWQ9ImxpbmUyZF82OSI+CiAgICAgIDxwYXRoIGQ9Ik0gNDczLjIzNjM2NCA0NC40NDM2MzYgCkwgNzc3LjYgNDQuNDQzNjM2IAoiIGNsaXAtcGF0aD0idXJsKCNwMjhhNGI2NWMzNCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNiMGIwYjA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICAgPC9nPgogICAgIDxnIGlkPSJsaW5lMmRfNzAiPgogICAgICA8Zz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI202NzhjZjUyMjgyIiB4PSI0NzMuMjM2MzY0IiB5PSI0NC40NDM2MzYiIHN0eWxlPSJzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44Ii8+CiAgICAgIDwvZz4KICAgICA8L2c+CiAgICAgPGcgaWQ9InRleHRfMzgiPgogICAgICA8IS0tIDEwMCAtLT4KICAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoNDQ3LjE0ODg2NCA0OC4yNDI4NTUpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzEiLz4KICAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzAiIHg9IjYzLjYyMzA0NyIvPgogICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8L2c+CiAgICAgPC9nPgogICAgPC9nPgogICAgPGcgaWQ9InRleHRfMzkiPgogICAgIDwhLS0gQ1BVIHV0aWxpemF0aW9uIFslXSAtLT4KICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg0NDEuMDY5MTc2IDE4OS44Mzc4MTMpcm90YXRlKC05MClzY2FsZSgwLjEgLTAuMSkiPgogICAgICA8ZGVmcz4KICAgICAgIDxwYXRoIGlkPSJEZWphVnVTYW5zLTZjIiBkPSJNIDYwMyA0ODYzIApMIDExNzggNDg2MyAKTCAxMTc4IDAgCkwgNjAzIDAgCkwgNjAzIDQ4NjMgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtN2EiIGQ9Ik0gMzUzIDM1MDAgCkwgMzA4NCAzNTAwIApMIDMwODQgMjk3NSAKTCA5MjIgNDU5IApMIDMwODQgNDU5IApMIDMwODQgMCAKTCAyNzUgMCAKTCAyNzUgNTI1IApMIDI0MzggMzA0MSAKTCAzNTMgMzA0MSAKTCAzNTMgMzUwMCAKegoiIHRyYW5zZm9ybT0ic2NhbGUoMC4wMTU2MjUpIi8+CiAgICAgICA8cGF0aCBpZD0iRGVqYVZ1U2Fucy02MSIgZD0iTSAyMTk0IDE3NTkgClEgMTQ5NyAxNzU5IDEyMjggMTYwMCAKUSA5NTkgMTQ0MSA5NTkgMTA1NiAKUSA5NTkgNzUwIDExNjEgNTcwIApRIDEzNjMgMzkxIDE3MDkgMzkxIApRIDIxODggMzkxIDI0NzcgNzMwIApRIDI3NjYgMTA2OSAyNzY2IDE2MzEgCkwgMjc2NiAxNzU5IApMIDIxOTQgMTc1OSAKegpNIDMzNDEgMTk5NyAKTCAzMzQxIDAgCkwgMjc2NiAwIApMIDI3NjYgNTMxIApRIDI1NjkgMjEzIDIyNzUgNjEgClEgMTk4MSAtOTEgMTU1NiAtOTEgClEgMTAxOSAtOTEgNzAxIDIxMSAKUSAzODQgNTEzIDM4NCAxMDE5IApRIDM4NCAxNjA5IDc3OSAxOTA5IApRIDExNzUgMjIwOSAxOTU5IDIyMDkgCkwgMjc2NiAyMjA5IApMIDI3NjYgMjI2NiAKUSAyNzY2IDI2NjMgMjUwNSAyODgwIApRIDIyNDQgMzA5NyAxNzcyIDMwOTcgClEgMTQ3MiAzMDk3IDExODcgMzAyNSAKUSA5MDMgMjk1MyA2NDEgMjgwOSAKTCA2NDEgMzM0MSAKUSA5NTYgMzQ2MyAxMjUzIDM1MjMgClEgMTU1MCAzNTg0IDE4MzEgMzU4NCAKUSAyNTkxIDM1ODQgMjk2NiAzMTkwIApRIDMzNDEgMjc5NyAzMzQxIDE5OTcgCnoKIiB0cmFuc2Zvcm09InNjYWxlKDAuMDE1NjI1KSIvPgogICAgICAgPHBhdGggaWQ9IkRlamFWdVNhbnMtMjUiIGQ9Ik0gNDY1MyAyMDUzIApRIDQzODEgMjA1MyA0MjI2IDE4MjIgClEgNDA3MiAxNTkxIDQwNzIgMTE3OCAKUSA0MDcyIDc3MiA0MjI2IDUzOSAKUSA0MzgxIDMwNiA0NjUzIDMwNiAKUSA0OTE5IDMwNiA1MDczIDUzOSAKUSA1MjI4IDc3MiA1MjI4IDExNzggClEgNTIyOCAxNTg4IDUwNzMgMTgyMCAKUSA0OTE5IDIwNTMgNDY1MyAyMDUzIAp6Ck0gNDY1MyAyNDUwIApRIDUxNDcgMjQ1MCA1NDM3IDIxMDYgClEgNTcyOCAxNzYzIDU3MjggMTE3OCAKUSA1NzI4IDU5NCA1NDM2IDI1MSAKUSA1MTQ0IC05MSA0NjUzIC05MSAKUSA0MTUzIC05MSAzODYyIDI1MSAKUSAzNTcyIDU5NCAzNTcyIDExNzggClEgMzU3MiAxNzY2IDM4NjQgMjEwOCAKUSA0MTU2IDI0NTAgNDY1MyAyNDUwIAp6Ck0gMTQyOCA0MzUzIApRIDExNTkgNDM1MyAxMDA0IDQxMjAgClEgODUwIDM4ODggODUwIDM0ODEgClEgODUwIDMwNjkgMTAwMyAyODM3IApRIDExNTYgMjYwNiAxNDI4IDI2MDYgClEgMTcwMCAyNjA2IDE4NTQgMjgzNyAKUSAyMDA5IDMwNjkgMjAwOSAzNDgxIApRIDIwMDkgMzg4NCAxODUzIDQxMTggClEgMTY5NyA0MzUzIDE0MjggNDM1MyAKegpNIDQyNTAgNDc1MCAKTCA0NzUwIDQ3NTAgCkwgMTgzMSAtOTEgCkwgMTMzMSAtOTEgCkwgNDI1MCA0NzUwIAp6Ck0gMTQyOCA0NzUwIApRIDE5MjIgNDc1MCAyMjE1IDQ0MDggClEgMjUwOSA0MDY2IDI1MDkgMzQ4MSAKUSAyNTA5IDI4OTEgMjIxNyAyNTUwIApRIDE5MjUgMjIwOSAxNDI4IDIyMDkgClEgOTMxIDIyMDkgNjQyIDI1NTEgClEgMzUzIDI4OTQgMzUzIDM0ODEgClEgMzUzIDQwNjMgNjQzIDQ0MDYgClEgOTM0IDQ3NTAgMTQyOCA0NzUwIAp6CiIgdHJhbnNmb3JtPSJzY2FsZSgwLjAxNTYyNSkiLz4KICAgICAgPC9kZWZzPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTQzIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNTAiIHg9IjY5LjgyNDIxOSIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTU1IiB4PSIxMzAuMTI2OTUzIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMjAiIHg9IjIwMy4zMjAzMTIiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03NSIgeD0iMjM1LjEwNzQyMiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTc0IiB4PSIyOTguNDg2MzI4Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNjkiIHg9IjMzNy42OTUzMTIiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy02YyIgeD0iMzY1LjQ3ODUxNiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTY5IiB4PSIzOTMuMjYxNzE5Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtN2EiIHg9IjQyMS4wNDQ5MjIiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy02MSIgeD0iNDczLjUzNTE1NiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTc0IiB4PSI1MzQuODE0NDUzIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNjkiIHg9IjU3NC4wMjM0MzgiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy02ZiIgeD0iNjAxLjgwNjY0MSIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTZlIiB4PSI2NjIuOTg4MjgxIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMjAiIHg9IjcyNi4zNjcxODgiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy01YiIgeD0iNzU4LjE1NDI5NyIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTI1IiB4PSI3OTcuMTY3OTY5Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNWQiIHg9Ijg5Mi4xODc1Ii8+CiAgICAgPC9nPgogICAgPC9nPgogICA8L2c+CiAgIDxnIGlkPSJsaW5lMmRfNzEiPgogICAgPHBhdGggZD0iTSA0ODcuMDcxMDc0IDQ0LjQ0MzYzNiAKTCA1NTYuMjQ0NjI4IDQ0LjQ0MzYzNiAKTCA2MjUuNDE4MTgyIDQ0LjQ0MzYzNiAKTCA2OTQuNTkxNzM2IDQ0LjQ0MzYzNiAKTCA3NjMuNzY1Mjg5IDQ0LjQ0MzYzNiAKIiBjbGlwLXBhdGg9InVybCgjcDI4YTRiNjVjMzQpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjMWY3N2I0OyBzdHJva2Utd2lkdGg6IDEuNTsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICA8L2c+CiAgIDxnIGlkPSJsaW5lMmRfNzIiPgogICAgPHBhdGggZD0iTSA0ODcuMDcxMDc0IDEwOS4yMjA2ODkgCkwgNTU2LjI0NDYyOCA3OC43NDkyNyAKTCA2MjUuNDE4MTgyIDcwLjU4NzkzOCAKTCA2OTQuNTkxNzM2IDY0LjE0Njg0MyAKTCA3NjMuNzY1Mjg5IDYzLjI5OTQ3OCAKIiBjbGlwLXBhdGg9InVybCgjcDI4YTRiNjVjMzQpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjZmY3ZjBlOyBzdHJva2Utd2lkdGg6IDEuNTsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICA8L2c+CiAgIDxnIGlkPSJsaW5lMmRfNzMiPgogICAgPHBhdGggZD0iTSA0ODcuMDcxMDc0IDIxMi40MTQzNTMgCkwgNTU2LjI0NDYyOCAxNDIuNTA2ODUgCkwgNjI1LjQxODE4MiAxMzcuMzgyOTY2IApMIDY5NC41OTE3MzYgMTMyLjc3NzE0OCAKTCA3NjMuNzY1Mjg5IDEyNS42MzA2OSAKIiBjbGlwLXBhdGg9InVybCgjcDI4YTRiNjVjMzQpIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjMmNhMDJjOyBzdHJva2Utd2lkdGg6IDEuNTsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICA8L2c+CiAgIDxnIGlkPSJsaW5lMmRfNzQiPgogICAgPHBhdGggZD0iTSA0ODcuMDcxMDc0IDI0Mi4xMTYzNjQgCkwgNTU2LjI0NDYyOCAxODYuMTY3OTE5IApMIDYyNS40MTgxODIgMTg0LjU1NDQ2NiAKTCA2OTQuNTkxNzM2IDE4Mi42MDM1NDcgCkwgNzYzLjc2NTI4OSAxNzMuMDc0NTc4IAoiIGNsaXAtcGF0aD0idXJsKCNwMjhhNGI2NWMzNCkiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICNkNjI3Mjg7IHN0cm9rZS13aWR0aDogMS41OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgIDwvZz4KICAgPGcgaWQ9InBhdGNoXzkiPgogICAgPHBhdGggZD0iTSA0NzMuMjM2MzY0IDI1MiAKTCA0NzMuMjM2MzY0IDM0LjU2IAoiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWpvaW46IG1pdGVyOyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgIDwvZz4KICAgPGcgaWQ9InBhdGNoXzEwIj4KICAgIDxwYXRoIGQ9Ik0gNzc3LjYgMjUyIApMIDc3Ny42IDM0LjU2IAoiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWpvaW46IG1pdGVyOyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgIDwvZz4KICAgPGcgaWQ9InBhdGNoXzExIj4KICAgIDxwYXRoIGQ9Ik0gNDczLjIzNjM2NCAyNTIgCkwgNzc3LjYgMjUyIAoiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICMwMDAwMDA7IHN0cm9rZS13aWR0aDogMC44OyBzdHJva2UtbGluZWpvaW46IG1pdGVyOyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgIDwvZz4KICAgPGcgaWQ9InBhdGNoXzEyIj4KICAgIDxwYXRoIGQ9Ik0gNDczLjIzNjM2NCAzNC41NiAKTCA3NzcuNiAzNC41NiAKIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjMDAwMDAwOyBzdHJva2Utd2lkdGg6IDAuODsgc3Ryb2tlLWxpbmVqb2luOiBtaXRlcjsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICA8L2c+CiAgIDxnIGlkPSJsZWdlbmRfMiI+CiAgICA8ZyBpZD0icGF0Y2hfMTMiPgogICAgIDxwYXRoIGQ9Ik0gNjk3LjE1NjI1IDI0NyAKTCA3NzAuNiAyNDcgClEgNzcyLjYgMjQ3IDc3Mi42IDI0NSAKTCA3NzIuNiAxODcuMjg3NSAKUSA3NzIuNiAxODUuMjg3NSA3NzAuNiAxODUuMjg3NSAKTCA2OTcuMTU2MjUgMTg1LjI4NzUgClEgNjk1LjE1NjI1IDE4NS4yODc1IDY5NS4xNTYyNSAxODcuMjg3NSAKTCA2OTUuMTU2MjUgMjQ1IApRIDY5NS4xNTYyNSAyNDcgNjk3LjE1NjI1IDI0NyAKegoiIHN0eWxlPSJmaWxsOiAjZmZmZmZmOyBvcGFjaXR5OiAwLjg7IHN0cm9rZTogI2NjY2NjYzsgc3Ryb2tlLWxpbmVqb2luOiBtaXRlciIvPgogICAgPC9nPgogICAgPGcgaWQ9ImxpbmUyZF83NSI+CiAgICAgPHBhdGggZD0iTSA2OTkuMTU2MjUgMTkzLjM4NTkzOCAKTCA3MDkuMTU2MjUgMTkzLjM4NTkzOCAKTCA3MTkuMTU2MjUgMTkzLjM4NTkzOCAKIiBzdHlsZT0iZmlsbDogbm9uZTsgc3Ryb2tlOiAjMWY3N2I0OyBzdHJva2Utd2lkdGg6IDEuNTsgc3Ryb2tlLWxpbmVjYXA6IHNxdWFyZSIvPgogICAgPC9nPgogICAgPGcgaWQ9InRleHRfNDAiPgogICAgIDwhLS0gMSBDUFVzIC0tPgogICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDcyNy4xNTYyNSAxOTYuODg1OTM4KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzEiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0yMCIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNDMiIHg9Ijk1LjQxMDE1NiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTUwIiB4PSIxNjUuMjM0Mzc1Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNTUiIHg9IjIyNS41MzcxMDkiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03MyIgeD0iMjk4LjczMDQ2OSIvPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJsaW5lMmRfNzYiPgogICAgIDxwYXRoIGQ9Ik0gNjk5LjE1NjI1IDIwOC4wNjQwNjMgCkwgNzA5LjE1NjI1IDIwOC4wNjQwNjMgCkwgNzE5LjE1NjI1IDIwOC4wNjQwNjMgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2ZmN2YwZTsgc3Ryb2tlLXdpZHRoOiAxLjU7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgIDwvZz4KICAgIDxnIGlkPSJ0ZXh0XzQxIj4KICAgICA8IS0tIDQgQ1BVcyAtLT4KICAgICA8ZyB0cmFuc2Zvcm09InRyYW5zbGF0ZSg3MjcuMTU2MjUgMjExLjU2NDA2MylzY2FsZSgwLjEgLTAuMSkiPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTM0Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMjAiIHg9IjYzLjYyMzA0NyIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTQzIiB4PSI5NS40MTAxNTYiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy01MCIgeD0iMTY1LjIzNDM3NSIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTU1IiB4PSIyMjUuNTM3MTA5Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNzMiIHg9IjI5OC43MzA0NjkiLz4KICAgICA8L2c+CiAgICA8L2c+CiAgICA8ZyBpZD0ibGluZTJkXzc3Ij4KICAgICA8cGF0aCBkPSJNIDY5OS4xNTYyNSAyMjIuNzQyMTg4IApMIDcwOS4xNTYyNSAyMjIuNzQyMTg4IApMIDcxOS4xNTYyNSAyMjIuNzQyMTg4IAoiIHN0eWxlPSJmaWxsOiBub25lOyBzdHJva2U6ICMyY2EwMmM7IHN0cm9rZS13aWR0aDogMS41OyBzdHJva2UtbGluZWNhcDogc3F1YXJlIi8+CiAgICA8L2c+CiAgICA8ZyBpZD0idGV4dF80MiI+CiAgICAgPCEtLSAxNiBDUFVzIC0tPgogICAgIDxnIHRyYW5zZm9ybT0idHJhbnNsYXRlKDcyNy4xNTYyNSAyMjYuMjQyMTg4KXNjYWxlKDAuMSAtMC4xKSI+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMzEiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zNiIgeD0iNjMuNjIzMDQ3Ii8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtMjAiIHg9IjEyNy4yNDYwOTQiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy00MyIgeD0iMTU5LjAzMzIwMyIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTUwIiB4PSIyMjguODU3NDIyIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNTUiIHg9IjI4OS4xNjAxNTYiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy03MyIgeD0iMzYyLjM1MzUxNiIvPgogICAgIDwvZz4KICAgIDwvZz4KICAgIDxnIGlkPSJsaW5lMmRfNzgiPgogICAgIDxwYXRoIGQ9Ik0gNjk5LjE1NjI1IDIzNy40MjAzMTIgCkwgNzA5LjE1NjI1IDIzNy40MjAzMTIgCkwgNzE5LjE1NjI1IDIzNy40MjAzMTIgCiIgc3R5bGU9ImZpbGw6IG5vbmU7IHN0cm9rZTogI2Q2MjcyODsgc3Ryb2tlLXdpZHRoOiAxLjU7IHN0cm9rZS1saW5lY2FwOiBzcXVhcmUiLz4KICAgIDwvZz4KICAgIDxnIGlkPSJ0ZXh0XzQzIj4KICAgICA8IS0tIDMyIENQVXMgLS0+CiAgICAgPGcgdHJhbnNmb3JtPSJ0cmFuc2xhdGUoNzI3LjE1NjI1IDI0MC45MjAzMTIpc2NhbGUoMC4xIC0wLjEpIj4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0zMyIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTMyIiB4PSI2My42MjMwNDciLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy0yMCIgeD0iMTI3LjI0NjA5NCIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTQzIiB4PSIxNTkuMDMzMjAzIi8+CiAgICAgIDx1c2UgeGxpbms6aHJlZj0iI0RlamFWdVNhbnMtNTAiIHg9IjIyOC44NTc0MjIiLz4KICAgICAgPHVzZSB4bGluazpocmVmPSIjRGVqYVZ1U2Fucy01NSIgeD0iMjg5LjE2MDE1NiIvPgogICAgICA8dXNlIHhsaW5rOmhyZWY9IiNEZWphVnVTYW5zLTczIiB4PSIzNjIuMzUzNTE2Ii8+CiAgICAgPC9nPgogICAgPC9nPgogICA8L2c+CiAgPC9nPgogPC9nPgogPGRlZnM+CiAgPGNsaXBQYXRoIGlkPSJwMDYzYzhmNWViOCI+CiAgIDxyZWN0IHg9IjEwOCIgeT0iMzQuNTYiIHdpZHRoPSIzMDQuMzYzNjM2IiBoZWlnaHQ9IjIxNy40NCIvPgogIDwvY2xpcFBhdGg+CiAgPGNsaXBQYXRoIGlkPSJwMjhhNGI2NWMzNCI+CiAgIDxyZWN0IHg9IjQ3My4yMzYzNjQiIHk9IjM0LjU2IiB3aWR0aD0iMzA0LjM2MzYzNiIgaGVpZ2h0PSIyMTcuNDQiLz4KICA8L2NsaXBQYXRoPgogPC9kZWZzPgo8L3N2Zz4K"
                    ]
                }
            },
            "cell_type": "markdown",
            "id": "463da0c9",
            "metadata": {},
            "source": [
                "**Result precomputed on the Sophia HPC cluster on a node with 32 CPUs.**\n",
                "\n",
                "![Optimization_time_cpuwt.svg](attachment:Optimization_time_cpuwt.svg)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "855f1c55",
            "metadata": {},
            "source": [
                "**Parallelization of gradients of WS, TI, Power and custom functions is not implemented yet**"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "d9f08646",
            "metadata": {},
            "source": [
                "## Precision\n",
                "\n",
                "**As default, PyWake simulates in double precision, i.e. 64 bit floating point values.**\n",
                "\n",
                "In some cases, however, single precision, i.e. 32 bit floating point values, may be sufficient and faster. \n",
                "\n",
                "In PyWake, the `Numpy32` context manager makes switching to single precition is very easy:"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 30,
            "id": "daeab853",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "float32\n",
                        "float32\n"
                    ]
                }
            ],
            "source": [
                "from py_wake.utils.numpy_utils import Numpy32\n",
                "\n",
                "with Numpy32():\n",
                "    print (np.array([1.,2,3]).dtype)\n",
                "    print (np.sin([1,2,3]).dtype)"
            ]
        },
        {
            "cell_type": "code",
            "execution_count": 31,
            "id": "0981f988",
            "metadata": {},
            "outputs": [
                {
                    "name": "stdout",
                    "output_type": "stream",
                    "text": [
                        "float64\n",
                        "float64\n"
                    ]
                }
            ],
            "source": [
                "# same with out context manager\n",
                "print (np.array([1.,2,3]).dtype)\n",
                "print (np.sin([1,2,3]).dtype)"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "152e64d3",
            "metadata": {},
            "source": [
                "    from py_wake.utils import layouts \n",
                "    from py_wake.utils.profiling import timeit\n",
                "    from tqdm.notebook import tqdm\n",
                "\n",
                "    n_lst = np.arange(50,550,50)\n",
                "    xy_lst = [layouts.rectangle(n,20,5*wt.diameter()) for n in n_lst]\n",
                "\n",
                "    t_lst_64 = [np.mean(timeit(wfm.aep, min_runs=10)(x,y)[1]) for x,y in tqdm(xy_lst)]\n",
                "\n",
                "    with Numpy32():\n",
                "        t_lst_32 = [np.mean(timeit(wfm.aep, min_runs=10)(x,y)[1]) for x,y in tqdm(xy_lst)]\n",
                "\n",
                "    ax1, ax2 = plt.subplots(1,2,figsize=(12,4))[1]\n",
                "    ax1.plot(n_lst, t_lst_64, label='Double precision')\n",
                "    ax1.plot(n_lst, t_lst_32, label='Single precision')\n",
                "    setup_plot(ax=ax1, ylabel='Time [s]',xlabel='No. wind turbines')\n",
                "    ax2.plot(n_lst, np.array(t_lst_64) / t_lst_32)\n",
                "    setup_plot(ax=ax2, ylabel='Speedup',xlabel='No. wind turbines')\n",
                "    plt.savefig('images/Optimization_precision.svg')"
            ]
        },
        {
            "cell_type": "markdown",
            "id": "c036a80c",
            "metadata": {},
            "source": [
                "**Result precomputed on the Sophia HPC cluster.**\n",
                "\n",
                "![image1.png](images/Optimization_precision.svg)"
            ]
        }
    ],
    "metadata": {
        "kernelspec": {
            "display_name": "Python 3 (ipykernel)",
            "language": "python",
            "name": "python3"
        },
        "language_info": {
            "codemirror_mode": {
                "name": "ipython",
                "version": 3
            },
            "file_extension": ".py",
            "mimetype": "text/x-python",
            "name": "python",
            "nbconvert_exporter": "python",
            "pygments_lexer": "ipython3",
            "version": "3.9.13"
        },
        "toc": {
            "base_numbering": 1,
            "nav_menu": {},
            "number_sections": true,
            "sideBar": true,
            "skip_h1_title": false,
            "title_cell": "Table of Contents",
            "title_sidebar": "Contents",
            "toc_cell": false,
            "toc_position": {
                "height": "calc(100% - 180px)",
                "left": "10px",
                "top": "150px",
                "width": "426.667px"
            },
            "toc_section_display": true,
            "toc_window_display": true
        }
    },
    "nbformat": 4,
    "nbformat_minor": 5
}